Humans have a remarkable ability to learn new concepts from just a handful of examples. Show a child a picture of a zebra once, and they can likely identify zebras in the wild, in cartoons, or in other photos. This is the essence of few-shot learning—a skill that comes naturally to us but has historically been a massive challenge for machines.

Traditional deep learning models are notoriously data-hungry. They require thousands, if not millions, of examples to master a task. When faced with a new problem and limited data, they often struggle, failing to generalize from the few examples they’re given. This is where meta-learning, or “learning to learn,” comes in. Instead of learning a single task from scratch, a meta-learning model learns from a wide variety of tasks, forming a strategy for learning that enables rapid adaptation to new, unseen tasks.

One of the most popular approaches in this area is Model-Agnostic Meta-Learning (MAML). The core idea behind MAML is to find a good set of initial model weights—a strong starting point. From this initialization, the model can quickly adapt to a new task using just a few steps of gradient descent. It’s like finding the perfect base camp on a mountain, from which many different peaks are easily reachable.

But what if we could learn more than just the base camp? What if we could also learn the best hiking trails—the optimal path to take for any given peak? This is the central question addressed by the paper Meta-learning the Learning Trends Shared Across Tasks. The researchers propose a new method called Path-Aware Meta-Learning (PAMELA), which doesn’t just learn a good starting point, but also learns how to adapt along the way. It captures the update directions, learning rates, and their evolution over time—effectively learning the entire learning trajectory.

In this article, we’ll take a deep dive into PAMELA. We’ll explore the limitations of previous methods, unpack how PAMELA works, and see how this innovative approach sets new benchmarks in few-shot learning.

The Landscape of Gradient-Based Meta-Learning

To appreciate PAMELA’s novelty, we must first understand its predecessors—particularly MAML and its extensions. These belong to the class of gradient-based meta-learning methods, which operate in two nested loops: an inner loop for task-specific adaptation, and an outer loop for meta-learning.

Imagine training a model for image classification. Instead of one massive dataset of cats and dogs, you create hundreds of mini-tasks. Each task might be a 5-way, 1-shot problem: “Here is one picture of a cat, dog, bird, car, and plane. Now identify new images belonging to these classes.”

  • Inner Loop: For each mini-task, you start with your current meta-learned weights \( \theta \) and perform a few gradient descent steps on that task’s small training set. This adapts the general model to the specifics of the current task, producing task-specific weights \( \theta' \).
  • Outer Loop: You then evaluate \( \theta' \) on a separate validation set for that task. The resulting error updates the original weights \( \theta \) such that future tasks can adapt even more effectively.

The goal, then, is to find an initialization \( \theta \) that’s highly adaptable—a set of weights from which quick learning happens naturally.

MAML and Meta-SGD: From Good Starts to Smarter Steps

MAML focuses on learning to initialize. It uses simple gradient descent with a fixed learning rate during adaptation. All its “meta” intelligence is in the initialization.

Meta-SGD extends this idea by learning a separate learning rate for each parameter. This acts as gradient preconditioning—modifying raw gradients to move more efficiently in parameter space.

Yet, both approaches share a limitation. MAML’s inner loop follows a static learning process, while Meta-SGD uses a single preconditioning matrix for all steps. In practice, learning behavior should change over time. Early steps should make large adjustments; later steps should fine-tune gradually. Neither MAML nor Meta-SGD captures this evolving trend.

Introducing PAMELA: Learning the Entire Path

PAMELA overcomes this limitation by making the learning process itself dynamic and learnable. Instead of fixed optimization rules, it learns how the trajectory of learning should evolve across inner-loop steps.

A comparison of the inner-loop optimization paths for MAML, Meta-SGD, and PAMELA. MAML follows true gradients, Meta-SGD takes one preconditioned step, and PAMELA takes multiple, uniquely preconditioned steps with skip connections.

Figure 1: Inner-loop optimization strategies. MAML (left) takes several steps along the standard gradient direction. Meta-SGD (middle) takes a single step in a meta-learned direction. PAMELA (right) takes multiple steps, each with a unique meta-learned direction and “gradient-skip” connections sharing information from past updates.

In PAMELA, each step in the inner loop has its own learned behavior. Instead of relying on static update rules, it learns how to learn dynamically.

Formally, PAMELA minimizes the validation loss after adaptation:

\[ \underbrace{\min_{\boldsymbol{\theta}, \boldsymbol{\Phi}} \mathbb{E}_{\mathcal{T} \sim P(\mathcal{T})} \left[ \mathcal{L}_{\mathcal{D}_{val}}\left( f_{\underbrace{\mathbf{F}_{\boldsymbol{\Phi}}(\boldsymbol{\theta})}_{inner-loop}} \right) \right]}_{outer-loop} \]

The function \( \mathbf{F}_{\Phi} \) represents PAMELA’s inner loop optimizer, parameterized by meta-parameters \( \Phi = \{Q, P^w\} \). These parameters make learning flexible and context-aware.

1. Step-Wise Learning Directions: \( Q \)

The first innovation is to learn distinct preconditioning matrices \( Q_j \) for each inner-loop step \( j \). Instead of a single global preconditioner as in Meta-SGD, PAMELA learns \( Q_0, Q_1, Q_2, \dots \) across steps.

This enables the meta-learner to adapt the magnitude and direction of updates over time. Early steps may involve large exploratory moves guided by \( Q_0 \), while later steps use smaller, precise adjustments guided by \( Q_4 \). In doing so, PAMELA captures how the pace of learning evolves across tasks.

2. Gradient-Skip Connections: \( P^w \)

The second key innovation brings context from the past. PAMELA incorporates gradient-skip connections, which mix current updates with parameter states from several steps ago.

Unlike ResNet’s skip connections (which link activations), PAMELA’s skips exist in parameter space. This helps the model maintain stability and avoid overfitting by blending recent updates with past parameter information.

The update rule combines both mechanisms:

\[ \boldsymbol{\theta}_{j+1} = \begin{cases} \boldsymbol{\theta}_j - \boldsymbol{Q}_j \circ \nabla_{\boldsymbol{\theta}_j} \mathcal{L}_{\mathcal{D}_{tr}}(f_{\boldsymbol{\theta}_j}) & \text{if } (j \text{ mod } w) \neq 0, \\ (1 - P_j^w) \circ \{\boldsymbol{\theta}_j - \boldsymbol{Q}_j \circ \nabla_{\boldsymbol{\theta}_j} \mathcal{L}_{\mathcal{D}_{tr}}(f_{\boldsymbol{\theta}_j})\} + P_j^w \circ \boldsymbol{\theta}_{j-w} & \text{else.} \end{cases} \]

Here, \( \circ \) is the element-wise product. When the condition \((j \text{ mod } w) \neq 0\) fails, PAMELA interleaves gradients from the current and previous steps using learnable coefficients \( P_j^w \), allowing the model to retain contextual memory of how previous adaptations turned out.

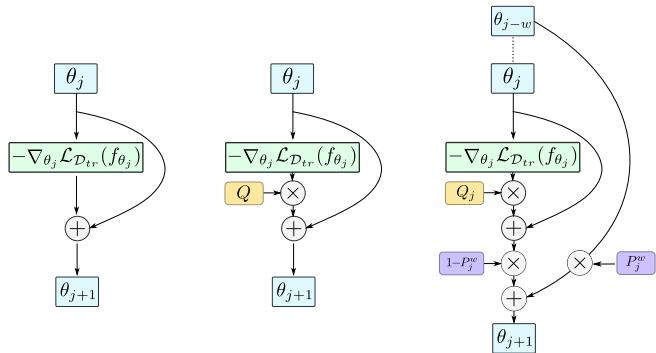
A schematic comparing inner-loop update rules for MAML, Meta-SGD, and PAMELA.

Figure 2: Comparison of inner-loop updates. MAML (left) applies a direct gradient step. Meta-SGD (middle) introduces a single preconditioning matrix \( Q \). PAMELA (right) learns a unique \( Q_j \) per step and blends parameters using \( P_j^w \), yielding richer adaptive dynamics.

The Outer Loop: Learning the Path-Finders

After completing the inner-loop updates, PAMELA evaluates the adapted model \( \theta_n \) on the validation set. The resulting loss is backpropagated through all inner steps, updating not only the initialization \( \theta \) but also each \( Q_j \) and \( P_j^w \):

[ {\boldsymbol{\theta}^{new}, \boldsymbol{\Phi}^{new}} = {\boldsymbol{\theta}, \boldsymbol{\Phi}}

  • \boldsymbol{\beta} \nabla_{{\boldsymbol{\theta}, \boldsymbol{\Phi}}} \sum_{k=1}^{K} \mathcal{L}{\mathcal{D}{val}^k}(f_{\boldsymbol{\theta}_n^k}) ]

This outer-loop ensures that PAMELA learns not only where to start, but also how to learn optimally along the path.

Putting PAMELA to the Test

Theory aside—does PAMELA’s sophistication actually lead to better results? The answer is a resounding yes, and the evidence comes from extensive experimentation on standard few-shot benchmarks.

Few-Shot Image Classification

The team evaluated PAMELA on three popular datasets: miniImageNet, CIFAR-FS, and tieredImageNet.

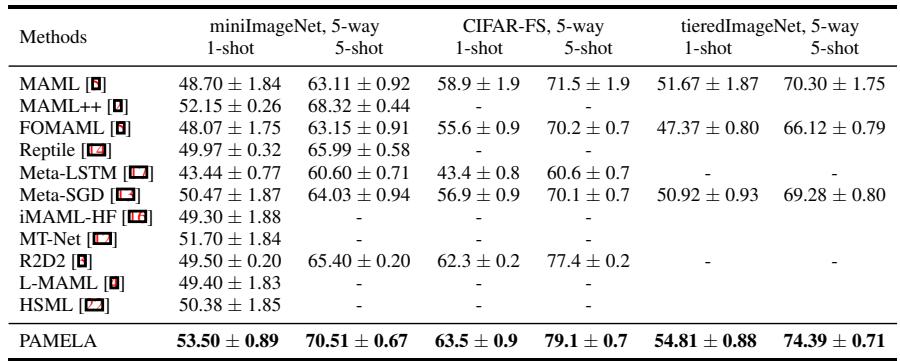
Table showing few-shot classification results on miniImageNet, CIFAR-FS, and tieredImageNet. PAMELA consistently outperforms other methods in both 1-shot and 5-shot settings.

Figure 3: Accuracy on few-shot classification tasks. PAMELA achieves consistent, state-of-the-art improvements across multiple benchmarks.

Across all datasets, PAMELA outperformed competing methods such as MAML, MAML++, and Meta-SGD. On miniImageNet 5-way 5-shot, it reached 70.51%, far exceeding MAML’s baseline \(63.11\%\). Similar gains appeared in the 1-shot setting and on CIFAR-FS and tieredImageNet. Learning the path of adaptation clearly yields better generalization.

Few-Shot Regression

To test adaptability beyond classification, the authors applied PAMELA to fitting sine waves—each with different amplitude, frequency, and phase. Each task provided only a handful of data points.

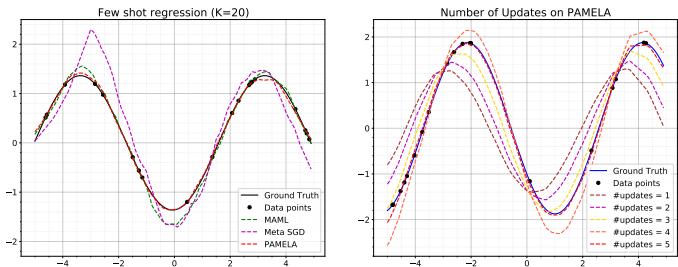
Results for the sine wave regression task. Left: PAMELA fits the ground truth better than MAML and Meta-SGD; middle: curve improves with more updates; right: PAMELA achieves the lowest MSE.

Figure 4: Sine wave regression results. PAMELA produces smoother and more precise fits than MAML and Meta-SGD, consistently achieving the lowest mean-squared error.

The results were illuminating. PAMELA’s curves aligned almost perfectly with the ground truth, correcting overshoots over successive updates, demonstrating how its learned trajectory enables self-correcting optimization behavior.

Why Does PAMELA Work? Insights from Ablation

To understand each component’s contribution, the authors conducted ablation experiments dissecting \( Q \) and \( P^w \).

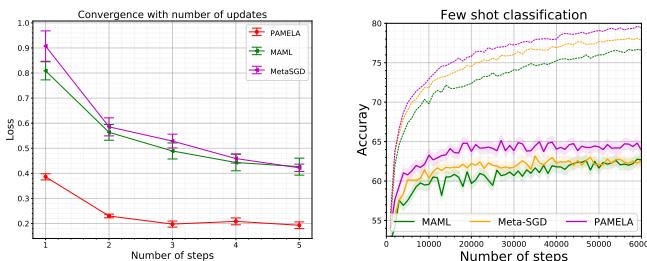
Comparative analysis of PAMELA’s performance and component contributions. Left: lower variance in inner-loop loss; middle: faster test accuracy improvement; right: ablation table breaking down contributions from Q and P^w.

Figure 5: PAMELA’s training dynamics and ablation study. Both step-specific preconditioning (\(Q\)) and skip connections (\(P^w\)) are critical. The full model delivers the highest accuracy with minimal complexity overhead.

Key observations:

  1. MAML Base: Achieves about 63.11% accuracy.
  2. MAML + Single \( Q \): Extending Meta-SGD to multiple steps drops performance (62.71%).
  3. MAML + Multiple \( Q_j \): Dynamic step-wise \( Q \) improves to 66.18%.
  4. MAML + \( P^w \): Gradient-skip alone boosts accuracy to 69.71%.
  5. Full PAMELA (Q + P^w): Combining both mechanisms achieves the best result—70.51%.

These findings confirm that PAMELA’s innovations are synergistic. Learning per-step dynamics and aggregating historical context together make for a more robust and generalizable meta-learner.

Model complexity remains reasonable as well:

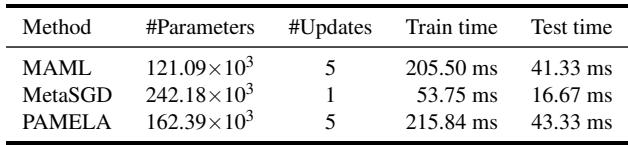
Comparison of parameters and computation times for MAML, Meta-SGD, and PAMELA.

Table 1: Complexity comparison. PAMELA adds modest parameters and minimal extra computation, making its performance gains practical.

PAMELA introduces about 34% more parameters than MAML but maintains similar training and inference times—a small tradeoff for consistent accuracy gains.

Conclusion: The Path Is the Goal

PAMELA marks a significant evolution in the philosophy of meta-learning. It shifts the focus from merely finding a good initialization to learning the entire adaptation path. By combining step-wise gradient preconditioning and context-preserving gradient-skip connections, PAMELA models how learning behavior changes over time across tasks.

This approach enables:

  • Dynamic learning behavior: Adjusting learning rates and directions at each step.
  • Contextual adaptation: Reusing past knowledge to regularize learning.
  • Faster convergence and better accuracy: Validated across multiple datasets.

In short, PAMELA doesn’t just learn where to begin—it learns how to proceed. As meta-learning research continues to grow, PAMELA shows that understanding the process of adaptation may unlock the next generation of truly human-like learning systems.