If you have ever tutored a student in mathematics, you know there is a distinct difference between memorization and understanding.
A student who memorizes might be able to solve a specific quadratic equation because they’ve seen that exact pattern fifty times. But if you ask them, “How would this change if the coefficient was negative?” or “Can you solve this using a different method?”, they crumble. They have the answer, but they don’t have the reasoning depth.
Large Language Models (LLMs) often suffer from this exact problem. While supervised fine-tuning has made them incredibly good at spitting out step-by-step solutions to standard math problems, they frequently lack the flexibility to handle follow-up questions or correct their own errors.
In this post, we are diving deep into a fascinating paper titled “Learn Beyond The Answer: Training Language Models with Reflection for Mathematical Reasoning.” This research proposes a shift in how we train models: instead of just feeding them more problems (breadth), we should train them to reflect on the problems they’ve already solved (depth).
The Breadth vs. Depth Problem
To understand the contribution of this paper, we first need to look at the current state of data augmentation in Large Language Models.
Data is the fuel of AI. In mathematical reasoning, high-quality human-annotated data is scarce and expensive. To get around this, researchers use Data Augmentation—using existing models (like GPT-4) to generate more training data for smaller models.
Traditionally, this happens in two ways:
- Question Augmentation (Q-Aug): Taking an existing question and tweaking the numbers or the scenario to create a new question.
- Answer Augmentation (A-Aug): Taking an existing question and asking a model to generate a new, perhaps clearer, solution path.
These methods operate on the principle of breadth. They assume that if the model sees enough variations of a problem, it will eventually generalize. However, the researchers behind this paper argue that stacking more instances doesn’t necessarily lead to a deeper understanding. It creates models that are good at “forward reasoning” (getting from A to B) but terrible at “reflective reasoning” (looking back at A and B to understand the relationship).
The authors propose a third way: Reflective Augmentation (RefAug).

As shown in Figure 1 above:
- (b) Question Augmentation adds new inputs (\(Q'_i\)).
- (c) Answer Augmentation adds new outputs (\(A'_i\)).
- (d) Reflective Augmentation changes the structure of the training data itself. It appends a Reflective Section (\(R_i\)) to the end of the answer.
What is Reflective Augmentation?
RefAug is inspired by human learning strategies. Educational psychology suggests that “overlearning”—practicing the same type of problem over and over—has diminishing returns. Instead, deep understanding comes from reflection: reviewing what was done, considering alternatives, and making connections to other concepts.
The method is surprisingly elegant in its implementation.
The Training Sequence
In a standard setting, a model is trained to predict the Answer (\(A\)) given a Question (\(Q\)). In RefAug, the model is trained to predict Answer + Reflection (\([A; R]\)) given the Question (\(Q\)).
The Reflection section isn’t just random text. The authors defined it based on educational theories by Stacey et al. (1982), requiring two specific components:
- Alternative Reasoning: The model must solve the same problem using a different method. This prevents rigid pattern matching.
- Follow-up Reasoning: The model must extend its understanding. This happens via:
- Abstraction: Generalizing the problem (e.g., replacing specific numbers with variables).
- Analogy: Creating and solving a harder, related problem.

Figure 3 illustrates this structure perfectly. Notice the flow:
- Original Problem: Find the maximum of a specific quadratic function.
- Initial Solution: Completing the square (standard method).
- Reflection (Alternative): Finding the derivative (calculus method).
- Reflection (Follow-up): Generalizing to \(ax^2 + bx + c\) (Abstraction) or solving a cubic function (Analogy).
By forcing the model to generate these reflections during training, the model essentially “meditates” on the math concepts. It learns that the answer isn’t just a string of tokens to be predicted, but the result of a flexible logical process.
The Inference Trick
You might be wondering: “Doesn’t generating all this extra text make the model slower when I actually use it?”
This is the clever part. The reflection is only for training.
During inference (testing/deployment), the model is given the question, and it generates the answer. Once it hits the marker that signals the start of the “Reflection” section, the generation is early-stopped.
The hypothesis is that the act of learning to predict the reflection updates the model’s internal weights in a way that improves the quality of the initial answer. The “wisdom” of the reflection is baked into the model’s neural pathways, even if it doesn’t output the text explicitly.
Why Reflection Beats Memorization: A Case Study
To see why this matters, let’s look at a specific algebraic example involving the substitution technique.
Substitution is a powerful tool in algebra, but models often memorize the look of a substitution problem without understanding the principle.

In Figure 2, we see a training problem: \((x-99)(x-101)=8\).
- Standard Training: The model sees the solution where \(t = x-100\). It learns a specific pattern: “find the number in the middle.”
- RefAug: The model sees the standard solution, plus an alternative (substituting \(t=x-99\)) and a follow-up. It learns that substitution is about simplifying the equation, not just finding a midpoint.
The Test: When faced with a new, harder problem \((7x+1)(9x+1)=61\), the standard model fails. It tries to substitute \(8x+1\) (the midpoint) but gets stuck because the math gets messy. The RefAug model, having a deeper conceptual understanding, recognizes it can multiply the terms to unify coefficients and then substitute, solving the problem correctly.
Experimental Results
The theory sounds sound, but does it work? The authors tested RefAug across several dimensions using models like Mistral-7B and Gemma-7B.
1. Standard Math Reasoning
First, they checked if RefAug helped with standard, single-round QA (like the GSM8k and MATH datasets). Even though the reflection isn’t generated during the test, the training impact was significant.
On average, RefAug improved accuracy by +7.2% over direct fine-tuning.
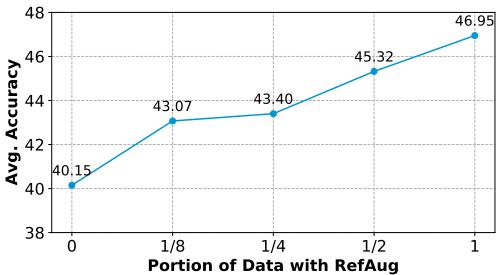
Figure 4 shows a clear trend: the more data you augment with reflection (from 0% to 100%), the better the model gets at standard math tasks. This confirms that the model isn’t just memorizing specific answers; it is becoming a better reasoner overall.
2. The “Reflective” Gap
The most dramatic results came from tasks that actually require deep thinking—specifically Follow-up QA (where the model has to answer a second and third question based on the first) and Error Correction (where the model has to fix a mistake).
Standard data augmentation (Q-Aug and A-Aug) essentially failed here. In some cases, adding more standard data actually hurt the model’s ability to correct errors. RefAug, however, excelled.
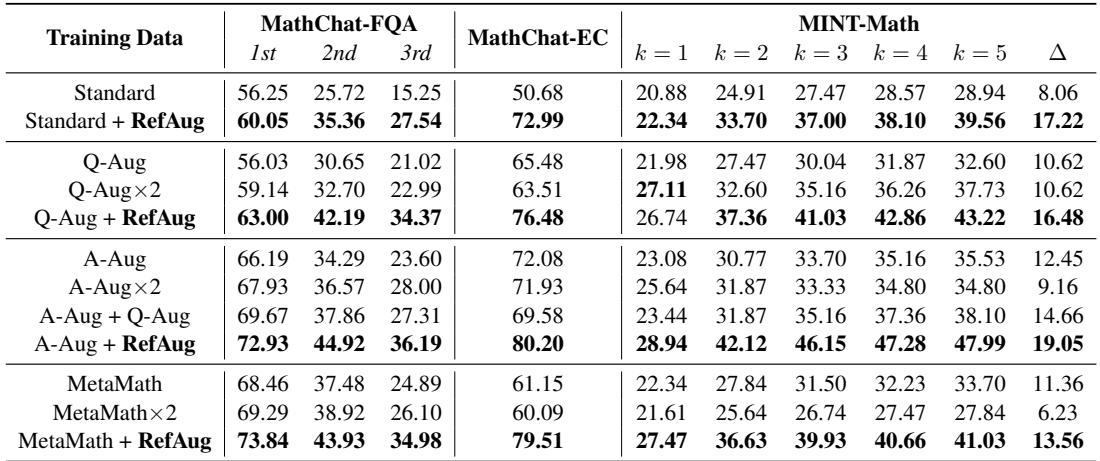
Looking at Table 2:
- MathChat-EC (Error Correction): Standard training scored 50.68%. RefAug jumped to 72.99%.
- MINT (Feedback): This benchmark measures if a model can improve its answer given feedback. RefAug significantly outperformed other methods, showing it had become more “coachable.”
This highlights a critical finding: You cannot brute-force deep understanding. simply generating 100,000 more math questions (Q-Aug) will not teach a model how to fix its own mistakes. You have to train it to look at problems from multiple angles.
3. Generalizing to Code
Math and coding are cousins in the AI world—both require strict logic and step-by-step execution. The researchers applied RefAug to code generation tasks (using HumanEval and MBPP benchmarks).
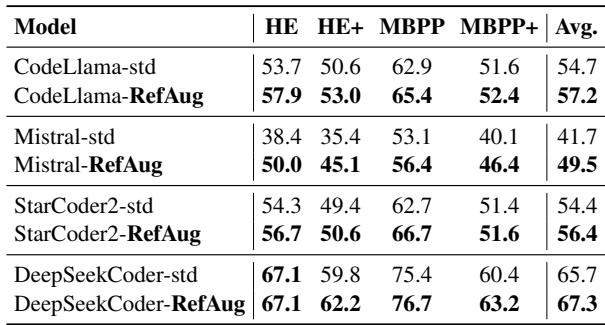
As Table 5 demonstrates, the benefits transferred beautifully. RefAug improved the performance of CodeLlama, Mistral, and StarCoder2. By asking the model to reflect on the code it just wrote (perhaps via abstraction or alternative implementation), the model became a better programmer.
Why This Matters
The “Learn Beyond The Answer” paper offers a pivotal correction to the current trajectory of LLM training. We are currently in an era of “Data Scarcity”—we are running out of high-quality human text to train on.
The industry’s knee-jerk reaction has been to use AI to generate massive amounts of synthetic data. But this paper warns us that volume is not enough. If we just use AI to generate millions of shallow Q&A pairs, we will create models that are broad but shallow—models that can pass a test but can’t explain why they are right or fix themselves when they are wrong.
Key Takeaways:
- RefAug is Complementary: You don’t have to choose between RefAug and other methods. The paper shows that combining Answer Augmentation with Reflective Augmentation yields the best results of all.
- Efficiency: Because the reflection is stripped out during inference, you get a smarter model without paying a latency tax during deployment.
- The “Teacher” Model Matters: The reflective sections in this paper were generated by GPT-4. The quality of the reflection is paramount. If the “teacher” gives bad analogies, the student will learn bad habits.
By embedding reflection into the training loop, we are moving closer to models that mimic the human learning process: solve, reflect, generalize, and master.
](https://deep-paper.org/en/paper/2406.12050/images/cover.png)