Beyond Storage: Unpacking the Math of Computation in Superposition

Introduction: The Crowded Mind of a Neural Network

If you’ve ever tried to understand what a neural network is “thinking,” you’ve likely encountered a perplexing phenomenon called polysemanticity—the tendency for a single neuron to activate in response to multiple, seemingly unrelated concepts. A neuron might respond to “cats,” “speed,” and the color “red,” all at once. For researchers working on mechanistic interpretability, this makes reverse-engineering networks incredibly challenging.

A leading explanation for this behavior is the superposition hypothesis, introduced by Chris Olah and collaborators. The hypothesis suggests that neural networks pack far more “features” or concepts into their activation spaces than they have dimensions—by encoding features as nearly orthogonal directions rather than assigning them to individual neurons. As long as only a few features are active at any time (i.e., the representations are sparse), the network can store this extra information without destroying separability.

Previous research largely viewed superposition as a storage mechanism—a way to compress representations and pass information through tight bottlenecks. But what if superposition isn’t just about storage? What if neural networks compute with features in superposition?

That question lies at the heart of “Mathematical Models of Computation in Superposition,” a recent theoretical paper that builds a rigorous mathematical framework for computation in superposition. Rather than treating superposition as merely a clever encoding trick, the authors show how neural networks can emulate complex logic circuits while their features remain compressed and entangled. The result is a blueprint for how networks might perform dense, efficient computation—one that could reshape our understanding of how modern AI “thinks.”

In this article, we’ll unpack the core ideas from the paper—starting from the basics of feature representation, moving through a construction that allows a single network layer to compute logical ANDs in superposition, and finally exploring how this capability can scale up to emulate entire deep circuits.

Background: What Does It Mean to “Represent” a Feature?

Before diving into computation, we need to understand what it means for a feature to be represented in a neural network. Suppose we have a network layer with d neurons, yet we believe that the activations encode m binary features, where m > d. The activation vector for an input \( x \) can be expressed as:

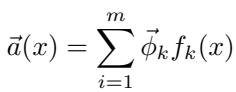
The activation vector \( \vec{a}(x) \) is a sum of feature vectors \( \vec{\phi}_k \), weighted by each feature’s binary presence \( f_k(x) \).

The challenge lies in reading these features back out of the tangled sum. To formalize this, the paper defines different levels of linear representation, which measure how reliably you can extract a feature’s value from activations.

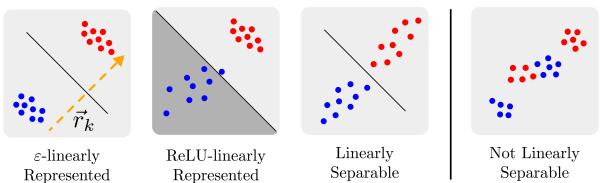
Figure 1: Visualizing different strength levels of feature representation. Red and blue points mark the feature’s presence or absence. The tighter and cleaner the separation, the stronger the representation.

1. Weakly Linearly Represented (Linearly Separable): A feature is weakly represented if you can draw a hyperplane that separates “on” activations from “off” ones. This definition is minimal—it ensures separability but not reliability. The margin between positive and negative examples can be arbitrarily small, making such features brittle for downstream computation.

2. ReLU-Linearly Represented: A stronger version, common in prior work, represents features that can be read by passing the activations through a ReLU layer and minimizing the average error between the output and the true feature values. This reads many features at once but allows small, averaged errors to hide poor representations for specific inputs.

3. ε-Linearly Represented: The strongest form used in this paper. A feature set is ε-linearly represented if each individual feature can be read by a vector \( \vec{r}_k \) such that its dot product with the activations is always within ε of the true binary value, across every input. This guarantees consistent precision rather than merely average correctness.

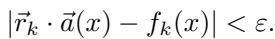
ε-linear representation demands that, for every input, the dot product between a read-off vector and activations stays tightly near 0 or 1.

Features that meet this strict criterion aren’t just identifiable—they’re computable. Once features are ε-linearly represented, logical operations like AND and OR can themselves become ε-linearly represented in subsequent layers. This compositional property breaks down for weaker definitions.

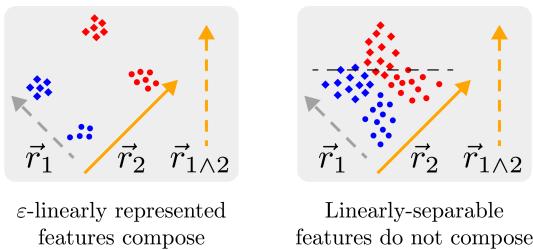
Figure 2: On the left, ε-linearly represented features can be reliably combined to compute new features (e.g., ANDs). On the right, weaker representations blur clusters so much that composition fails.

With this formalism, the authors can now demonstrate how neurons in superposition can not only store but process information.

From Representation to Computation: The Universal AND Circuit

The paper’s first major construction tackles a deceptively simple task: computing the logical AND between all possible pairs of features. Given m input features, there are \( \binom{m}{2} \) pairwise ANDs to compute—a task known as the Universal AND (U-AND) circuit.

The Naive Solution

When inputs are binary, you can compute \( x_i \wedge x_j \) with a single ReLU neuron as \( \text{ReLU}(x_i + x_j - 1) \). The most straightforward network builds one such neuron for every pair:

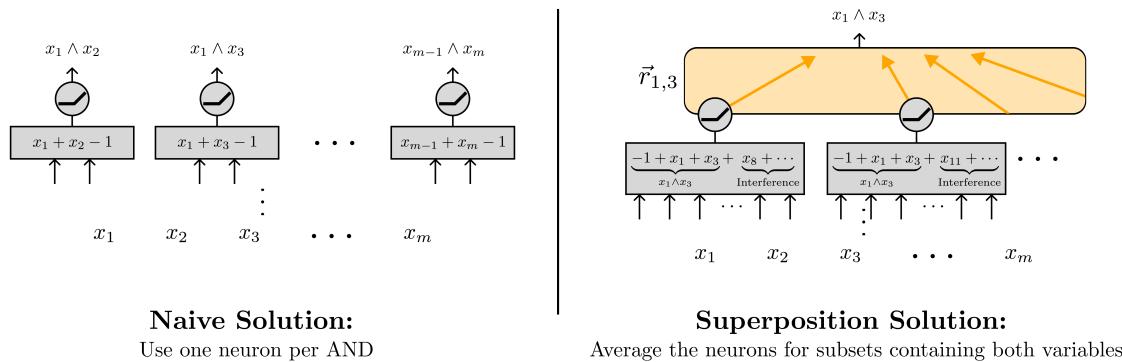
Figure 3: Left—Naive solution: one neuron per AND, scaling as \( O(m^2) \). Right—Superposition solution: neurons each check random subsets, drastically reducing the total count.

This naive approach scales quadratically: \( O(m^2) \) neurons to compute all pairwise ANDs. It’s simple but wasteful.

The Superposition Solution

The paper’s elegant reconstruction uses superposition and sparsity to achieve massive efficiency gains.

1. Random Subset Checking Each neuron activates if at least two inputs in a random subset are on, e.g., \( \text{ReLU}(b_1 + b_3 + b_8 + \dots - 1) \). Every neuron no longer corresponds to a single pairwise AND—it contributes distributed information across many.

2. Sparsity Assume that, for any input, at most s features are active. Sparse inputs limit the amount of interference between overlapping subsets.

3. Averaging Readouts For a specific pair \( (b_k, b_\ell) \), we can retrieve their AND by averaging the activations of neurons whose subsets included both features. Noise cancels in expectation, leaving the true pairwise contribution intact.

The mathematics show that if neurons sample subsets randomly, interference terms shrink with width \( d \), allowing the network to approximate all pairwise ANDs with high accuracy. The paper proves:

Theorem 2 (U-AND with Inputs in Superposition): A one-layer MLP can ε-linearly represent the Universal AND circuit for m features using only \( d = \tilde{O}(\sqrt{m}/\varepsilon^2) \) neurons—even when inputs themselves are in superposition.

This is extraordinary. The outputs number \( O(m^2) \), yet the network’s width scales only as \( \tilde{O}(\sqrt{m}) \). Computation explodes in richness without requiring more neurons.

Can Real Networks Do This?

Surprisingly, yes. The paper proves that even randomly initialized networks possess the capacity to perform U-AND-like computations.

Theorem 3 (Randomly Initialized MLPs): For wide enough layers, random one-layer MLPs ε-linearly represent the Universal AND circuit with high probability.

In other words, this superpositional computation isn’t a fragile fluke—it’s a natural outcome of standard neural architectures. Networks are born capable of these dense logical operations; training merely tunes the interference patterns into coherent functionality.

From U-AND to Arbitrary Computation: Scaling the Framework

The Universal AND provides the building block for general computation. Any boolean function can be written as a combination of AND terms (its Disjunctive Normal Form). With a mechanism for efficiently computing all pairwise—and even multiway—ANDs, a network can emulate any boolean circuit.

High Fan-In ANDs

The U-AND concept extends naturally to higher-order conjunctions. A single layer can compute ANDs of triples, quadruples, and more, by modifying how neurons combine subsets. Each AND term remains ε-linearly represented.

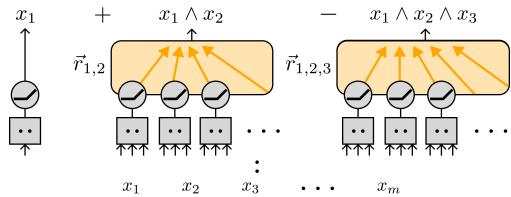
Figure 4: Building more complex boolean circuits. By combining ANDs through additive and subtractive operations, an MLP can represent arbitrary compositions of boolean features.

The authors prove:

Theorem 6: For any sparse boolean circuit of depth L, there exists a single-layer MLP of width \( \tilde{O}(\sqrt{m}) \) that ε-linearly represents its output.

The only drawback is that computing all possible conjunctions requires exponentially many neurons as depth increases.

Going Deep with Error Correction

To tame this exponential growth, the researchers propose composing multiple layers—alternating U-AND layers with error correction layers.

• Computation layer: Performs the logical operations (e.g., all pairwise ANDs).
• Error correction layer: Cleans up accumulated interference, restoring feature purity without expanding width.

Each error correction layer reduces interference ε to ε/c, keeping noise bounded across depth.

Theorem 8: Any sparse boolean circuit of width m and polynomial depth L can be ε-linearly represented by a deep neural network with width \( d = \tilde{O}(m^{2/3} s^2) \) and depth \( 2L \).

This result completes the framework: deep computation, compactly encoded and continuously self-correcting within superposition.

Implications for Mechanistic Interpretability

The mathematical constructions carry profound implications for how we analyze real neural networks.

1. Beware of “Unused” Features

The fact that random networks naturally represent complex logical conjunctions suggests that many identifiable features might exist even when they serve no purpose. Linear probes and sparse autoencoders could discover directions corresponding to “concepts” simply because such directions mathematically exist—not because they are used in computation. A feature being detectable doesn’t guarantee it’s utilized.

2. Look for Error Correction Motifs

Efficient computation in superposition demands mechanisms for error correction. Real networks performing similar compressed algorithms might exhibit nonlinear layers that stabilize activations—snapping noisy representations back toward consistent states. Empirical evidence from recent interpretability research (e.g., activation “plateaus” observed in GPT-2) may already hint at such structures.

Limitations and Future Directions

While elegant, the presented model has constraints:

• Binary Features Only: Real neural networks process continuous and multi-valued features, not pure booleans.
• Sparsity Assumption: The theoretical benefits hinge on sparse activations. Whether typical transformer or vision models meet these conditions remains an open question.
• Idealized Read-Offs: ε-linear representation is a strong assumption—it may oversimplify how actual learned features interact.

Future work could extend these results to continuous or probabilistic feature spaces, relaxing sparsity assumptions or adapting the framework to empirical data.

Conclusion

“Mathematical Models of Computation in Superposition” reframes superposition from a passive phenomenon of storage to an active mechanism of computation. Through the Universal AND and its extensions, the authors show how networks can perform immense logical operations on features compressed within a lower-dimensional space—using far fewer neurons than naïve architectures would suggest.

At its core, the paper teaches us that in the crowded minds of neural networks, computation doesn’t necessarily happen between neurons—it happens within the cloud of superposed features they collectively represent. Understanding this hidden layer of logic may be key to unlocking a more transparent, mechanistic account of how AI systems truly process information.