Deep learning has transformed computer vision, but its success often depends on abundant labeled data. Models trained on massive datasets like ImageNet can classify thousands of objects accurately—but what happens when we want to teach a model a new concept with only a few examples? For instance, recognizing a rare bird species from just five photos. This challenge defines few-shot learning (FSL).

Humans can generalize from a single example, but deep models struggle with limited data and tend to overfit. Metric-based few-shot learning methods address this by learning a feature space where similar images cluster together. A new “query” image is classified by finding the closest labeled “support” examples in that space.

However, these methods face a persistent problem: background noise. Every image contains not only the subject but also surrounding elements—the branch a bird sits on, the grass beneath, or the sky behind it. When a model learns the concept “bird,” it might mistakenly associate the background with the bird itself. How can we teach it to focus on the subject and ignore distractions?

A recent research paper, Feature Aligning Few Shot Learning Method Using Local Descriptors Weighted Rules, proposes an elegant solution. The authors introduce FAFD-LDWR, a method that intelligently filters out irrelevant visual information. By aligning key local descriptors of support and query images, it focuses on discriminative image regions and improves classification accuracy across multiple benchmarks.

In this post, we explore how FAFD-LDWR works step-by-step.

The Problem with Background Clutter

Modern vision models analyze images through smaller patches, generating local descriptors—feature vectors representing localized regions. This preserves fine-grained detail but also captures irrelevant areas.

Examples of birds with red boxes marking relevant semantic regions and yellow boxes marking background areas.

Figure 1. Regions relevant (red) and irrelevant (yellow) to image classes.

Each image includes descriptors tied to crucial semantic regions (e.g., feathers, beak) and others linked to clutter (e.g., branches, grass). Treating all descriptors equally introduces heavy noise.

Previous approaches combined global and local features to mitigate this issue, but those methods increased model complexity. FAFD-LDWR instead directly filters irrelevant descriptors, aligning useful parts of images for clearer class distinctions.

The FAFD-LDWR Method: A Three-Stage Pipeline

The FAFD-LDWR framework, illustrated below, extracts, refines, and filters features for precise few-shot classification through three modules:

  1. Embedding Feature Extraction – Generates local descriptors using a neural backbone.
  2. Cross Normalization – Retains discriminative details through adaptive multi-level normalization.
  3. Local Descriptors with Dynamically Weighted Rules (LDWR) – Evaluates descriptor importance and filters noise.

Schematic of the FAFD-LDWR framework for 5-way 1-shot classification.

Figure 2. Overview of the FAFD-LDWR pipeline.

Let’s explore each component.

Step 1: Extracting Local Descriptors

FAFD-LDWR starts by feeding an image through a convolutional neural network (Conv-4 or ResNet-12) to generate local descriptor tensors of size \( C \times H \times W \), where \(C\) is the number of channels.

\[ \mathcal{A}_{\phi}(I) = [\mathbf{x}^1, ..., \mathbf{x}^N] \in \mathbb{R}^{C \times N} \]

Here, \(N = H \times W\). Each \(\mathbf{x}^i\) encodes information about a specific region in the image. This representation retains spatial relationships essential for fine-grained recognition tasks.

Step 2: Cross Normalization for Better Feature Representation

Normalization stabilizes training and balances feature scales. Common L2 normalization, however, can suppress fine details important for class discrimination. FAFD-LDWR introduces cross normalization, merging spatial and channel-level approaches using adaptive weights.

Spatial-level normalization focuses on individual descriptor positions:

\[ x_s = \left( \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \right) \cdot \operatorname{conv1}(\operatorname{map}) + \operatorname{conv2}(\operatorname{map}) \]

Channel-level normalization adjusts each feature channel across spatial locations:

\[ x_c = \gamma \times \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta \]

Results from both processes are fused:

\[ x_{CN} = x_s \times \frac{\omega_1}{\omega_1 + \omega_2} + x_c \times \frac{\omega_2}{\omega_1 + \omega_2} \]

This adaptive blend preserves locally discriminative information and enhances robustness—an ideal foundation for filtering operations.

Step 3: Filtering with Local Descriptors Weighted Rules (LDWR)

At the heart of FAFD-LDWR is dynamic filtering using Local Descriptors Weighted Rules (LDWR). Each descriptor receives an “importance score” based on neighborhood context and similarity to class prototypes.

Creating Neighborhood Representations

To increase stability, each local descriptor \(q\) is replaced with a neighborhood representation, averaging its \(k\) nearest neighbors by cosine similarity:

\[ \operatorname{similarity}(q, x_i) = \frac{q \cdot x_i}{|q||x_i|} \]

\[ N_q = \frac{1}{k} \sum_{i \in NN_k(q)} x_i \]

This step smooths noise and incorporates contextual information for greater reliability.

Scoring and Filtering Descriptors

  1. Compute Class Prototypes: The prototype for each class aggregates all descriptors, representing a generalized semantic center.
\[ P_c = \frac{1}{|S_c|} \sum_{x \in S_c} f_\theta(x) \]
  1. Calculate Similarity Scores: For every descriptor neighborhood representation \(N_i\), compute its similarity to prototype \(P_c\):
\[ S_{i,c} = \frac{N_i \cdot P_c}{\|N_i\|\|P_c\|} \]
  1. Aggregate Importance and Threshold: Average cosine similarities across classes to derive an importance weight:
\[ \overline{\omega}_i = \frac{1}{K} \sum_{c=1}^{K} S_{i,c} \]

Then compute global mean and standard deviation:

\[ \overline{\mu} = \frac{1}{M \times T} \sum_{m=1}^{M} \sum_{n=1}^{T} \overline{\omega}_{n,m} \]

\[ \overline{\sigma} = \sqrt{\frac{1}{M \times T} \sum_{m=1}^{M} \sum_{n=1}^{T} (\overline{\omega}_{n,m} - \overline{\mu})^2} \]
  1. Apply the 3σ Rule: Descriptors with similarity below \(\overline{\mu} - \overline{\sigma}\) are filtered out as irrelevant noise.
\[ S_{i,c} < (\overline{\mu} - \overline{\sigma}) \]

Filtering occurs iteratively—support set descriptors are cleaned first, refreshed prototypes are recalculated, and then query descriptors are filtered accordingly.

Step 4: Classification Using Clean Descriptors

After filtering, only meaningful descriptors remain. Classification compares query descriptors to filtered prototypes using cosine similarity over top neighbors:

\[ \text{Similarity}(q, \text{category}_i) = \sum_{l=1}^{L} \sum_{j=1}^{k} \cos(\hat{\mathbf{x}}_q^l, m_j^i) \]

Finally, softmax transforms similarity into probabilistic classification:

\[ P(c = i|q) = \frac{\exp(\text{Similarity}(q, \text{category}_i))}{\sum_{i=1}^{5} \exp(\text{Similarity}(q, \text{category}_i))} \]

This approach prioritizes key regions (e.g., the bird’s body rather than the surrounding foliage), resulting in more accurate predictions.

Experimental Results: How Well Does It Work?

FAFD-LDWR was evaluated on three fine-grained few-shot benchmarks: CUB-200 (birds), Stanford Dogs, and Stanford Cars. Each dataset demands attention to subtle visual features—ideal for testing descriptor filtering.

General Few-Shot Performance

The ResNet-12 backbone produced standout results, outperforming 13 state-of-the-art baselines in both 1-shot and 5-shot tasks.

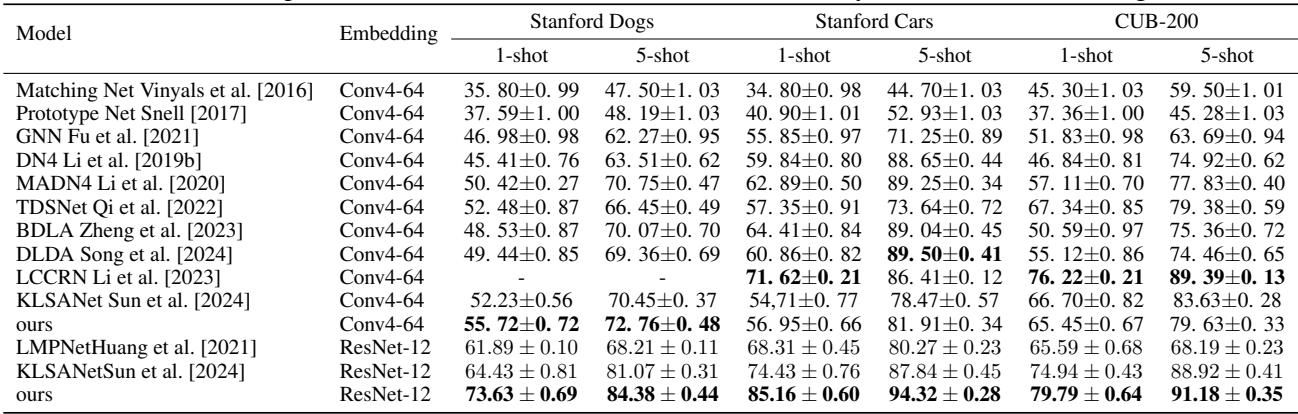
Comparison table showing FAFD-LDWR achieving top accuracy across benchmarks.

Table 1. FAFD-LDWR outperforms previous methods in fine-grained few-shot classifications.

ResNet-12’s higher descriptor count lets FAFD-LDWR’s dynamic weighting work effectively, removing redundant background patches and capturing discriminative features precisely.

Cross-Domain Generalization

True robustness lies in cross-domain adaptability. FAFD-LDWR was trained on miniImageNet and tested on CUB birds, a challenging transfer scenario.

Cross-domain comparison showing FAFD-LDWR leading alternative methods.

Table 2. FAFD-LDWR surpasses multiple competitors in miniImageNet → CUB experiments.

FAFD-LDWR’s focus on semantic alignment rather than dataset-specific textures enables impressive transferability across domains, proving its general learning capability.

Ablation Studies: Understanding Each Component

The researchers conducted ablations to confirm the contribution of each innovation.

  • Neighborhood Representation Boost: Using averaged neighborhood descriptors (W) improves accuracy compared to raw ones (w/o). Neighborhood representation improves accuracy by smoothing local noise.

Table 3. Impact of neighborhood representation on performance.

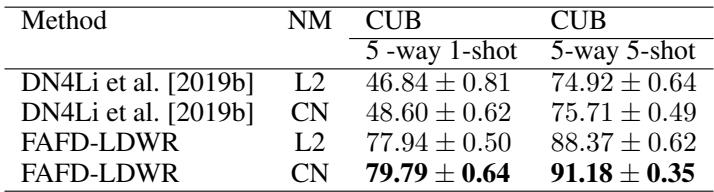
  • Cross Normalization Advantage: Replacing standard L2 normalization with cross normalization (CN) enhances classification in both DN4 and FAFD-LDWR. Cross Normalization shows superior results compared to L2 normalization.

Table 4. Benefit of cross normalization over L2 normalization.

  • Optimal Number of Neighbors: Accuracy peaks at k=10 neighbors, as seen below. Too few reduce smoothing; too many reintroduce noise.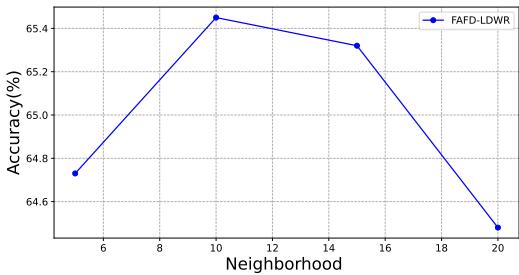 Accuracy curve showing peak performance at k=10 neighbors.

Figure 3. Accuracy versus number of neighbors in neighborhood representation.

FAFD-LDWR consistently demonstrates that careful descriptor filtering and normalization deliver meaningful improvements without extra parameters.

Conclusion and Key Takeaways

The FAFD-LDWR method provides a simple yet powerful way to enhance few-shot learning by filtering out irrelevant local descriptors. Rather than complex architectures or heavy optimization, it focuses on aligning feature semantics between support and query images.

Key Insights:

  1. Noise is a Primary Obstacle – Background regions dilute discriminative signals in metric-based FSL.
  2. Filtering Enhances Clarity – Dynamically weighted selection removes irrelevant descriptors and refines feature matching.
  3. Adaptive Preprocessing Matters – Cross normalization and contextual neighborhood averaging prepare descriptors for accurate alignment.

By strategically focusing on meaningful parts of images, FAFD-LDWR achieves state-of-the-art few-shot recognition across challenging datasets—extending the horizon for learning from minimal examples.