Meta-learning, or “learning to learn,” is one of the most exciting frontiers in machine learning. Its promise lies in enabling models to adapt quickly to new tasks using just a few examples—a crucial ability in fields such as personalized robotics, few-shot image classification, and adaptive healthcare systems.

Most popular meta-learning approaches, including the well-known Model-Agnostic Meta-Learning (MAML) algorithm, revolve around a simple but elegant concept: learn a good model initialization. The idea is that if the initial parameters are already close to optimal for a variety of tasks, then adapting to a new task should only require a slight adjustment—perhaps just one or two gradient descent steps. This “good initialization” principle forms the backbone of many bi-level optimization frameworks, which consist of an inner loop (task-specific adaptation) and an outer loop (meta-update based on how well the adaptation performed).

However, what if this core assumption—the “one-step is enough” rule—is both theoretically convenient and practically flawed? The research paper “Rethinking Meta-Learning from a Learning Lens” challenges this assumption, showing that this reliance on single-step adaptation often causes underfitting on complex tasks and overfitting on simple ones.

To overcome these issues, the authors propose a new lens—a shift in perspective. They urge us to rethink what a meta-learning model truly is and introduce a plug-and-play technique called TRLearner (Task Relation Learner), which uses relationships between tasks to calibrate learning. By enforcing consistency among related tasks, TRLearner helps models focus on meaningful information, rather than being constrained by the rigidity of one-step updates.

In this article, we’ll unpack the paper’s ideas and journey through its reasoning:

  • Why the “good initialization” view can fail in practice.
  • The redefined meta-learning framework through the Learning Lens.
  • How TRLearner extracts and uses task relationships to improve training.
  • Experimental results demonstrating TRLearner’s impact across domains.

The Standard Meta-Learning Framework

To understand what changes, we need to understand the starting point.

Most modern meta-learning algorithms operate under a bi-level optimization procedure. The process begins with a distribution of tasks, denoted \(p(\mathcal{T})\). Each training batch samples several tasks \( \tau_i \), each having its own mini-dataset divided into a support set (for adaptation) and a query set (for evaluation).

The global model \( \mathcal{F}_{\theta} \) undergoes training in two stages:

1. Inner Loop (Task Adaptation): For every sampled task \( \tau_i \), the model adapts from \( \mathcal{F}_{\theta} \) using its support set \( \mathcal{D}_i^s \), often with just one gradient descent step:

\[ f_{\theta}^{i} \leftarrow \mathcal{F}_{\theta} - \alpha \nabla_{\mathcal{F}_{\theta}} \mathcal{L}(\mathcal{D}_{i}^{s}, \mathcal{F}_{\theta}) \]

Here, \( \alpha \) is the step size, and \( \mathcal{L} \) measures task-specific loss. A good initialization means that this single step already yields a high-performing task-specific model \( f_{\theta}^{i} \).

2. Outer Loop (Meta-Update): After all tasks are adapted, the performance is evaluated using each task’s query set \( \mathcal{D}_{i}^{q} \). The aggregated query loss is backpropagated to update the global model:

\[ \mathcal{F}_{\theta} \leftarrow \mathcal{F}_{\theta} - \beta \nabla_{\mathcal{F}_{\theta}} \frac{1}{N_{tr}} \sum_{i=1}^{N_{tr}} \mathcal{L}(\mathcal{D}_{i}^{q}, f_{\theta}^{i}) \]

Where \( \beta \) is the “meta” learning rate. Because \( f_{\theta}^{i} \) depends on \( \mathcal{F}_{\theta} \), this process involves second-order differentiation.

While powerful, this approach assumes that one gradient step is a sufficient proxy for learning—a simplification that often fails for complex real-world tasks.

When One Step Isn’t Enough

There’s a paradox here: the training process seeks an optimal task-specific model, yet only allows a single inner-loop gradient step. This mismatch between the model’s intended capacity and its actual adaptation behavior leads to modeling errors.

To demonstrate the impact, the authors conducted an experiment using tasks with varying complexity from the miniImageNet dataset. Each meta-learning model was trained using a fixed “one-step” configuration.

Four line graphs showing the training and testing accuracy for MAML on four datasets (D1–D4)

“Performance of MAML on tasks of different complexities. Tasks D1 and D2 show slow test accuracy improvement (underfitting), while simpler tasks D3 and D4 show overfitting with diverging test accuracy.”

The results reveal two distinct behaviors:

  • On complex tasks — test accuracy slowly improves even after training converges, showing the model cannot sufficiently learn with one step (underfitting).
  • On simple tasks — training accuracy rises rapidly, but test accuracy deteriorates (overfitting).

The takeaway: the fixed “one-step learning” assumption is too rigid. The right number of adaptation steps should depend on task complexity.

Rethinking Meta-Learning: The Learning Lens

To move beyond the limitations of fixed adaptation, the paper redefines the nature of meta-learning.

Instead of viewing \( \mathcal{F}_{\theta} \) merely as a parameter initialization, they treat it as a function that maps a task to a task-specific model, i.e.,

\[ \mathcal{F}_{\theta}(\tau_i) = f_{\theta}^{i} \]

Conceptually, this turns \( \mathcal{F}_{\theta} \) into a generator that produces models tailored to each task.

How can one design a model that outputs other models? A massive MLP could theoretically learn this mapping, but its parameter size would be impractical. The authors instead rely on a clever trick: make gradient descent itself part of the model through a non-linear meta-layer.

Under this framework, the meta-learning model has two components:

  1. Model Initialization Layers — conventional neural layers (e.g., ResNet) for feature extraction.
  2. Meta-Layer(s) — non-linear layers implemented using gradient updates that allow expressive adaptation.

A diagram showing the proposed model structure. Part (a)

“Modeling of the meta-learning system \( \mathcal{F}_{\theta} \): (a) shows how tasks pass through initialization and meta-layers to produce task-specific models, (b) depicts forward and backward optimization with support and query sets.”

This interpretation gives the model flexibility—extra meta-layers can strengthen learning for complex tasks, while fewer meta-layers reduce overfitting in simpler ones. Yet, deciding the optimal number of meta-layers for every scenario is still difficult. The paper therefore proposes an intelligent alternative: control the information flow between tasks during training.

Using Task Relations to Regulate Learning: TRLearner

Rather than change architectures dynamically, the authors focus on regulating how the model learns across tasks. Their key theoretical insight (Theorem 1) shows that the classifier for one task can improve by leveraging features from other similar tasks.

This observation leads to TRLearner (Task Relation Learner), a method that infers similarities among tasks and uses those relationships to regularize training. Essentially, TRLearner encourages the model to behave similarly across related tasks—capturing shared, important features while minimizing task-specific noise.

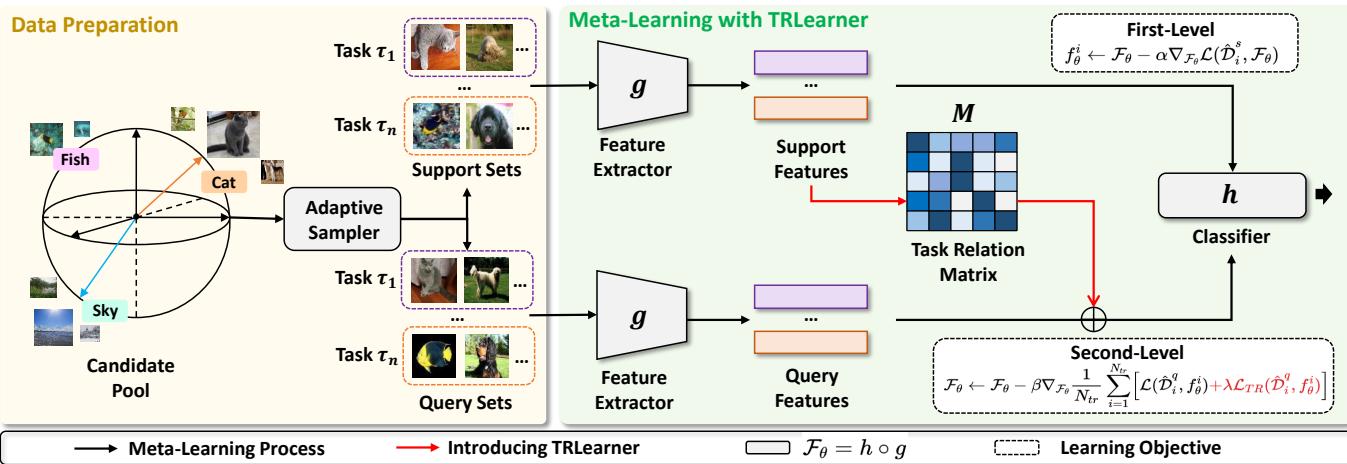
A flowchart of the TRLearner framework.

“Framework of meta-learning with TRLearner: data sampling, feature extraction, task relation matrix construction, and relation-aware optimization.”

TRLearner operates in two core steps:

1. Extracting Task Relations

A task relation matrix \( \mathcal{M} = \{m_{ij}\} \) quantifies similarity between each pair of tasks. Directly comparing all samples can be unreliable, so the method uses an adaptive sampler to collect representative meta-data for each task. These meta-data \( \hat{\mathcal{D}}_{i}^{s} \) pass through the feature extractor \( g \) to form task representations, then a multi-headed similarity layer computes similarity:

\[ m_{i,j} = \frac{1}{K} \sum_{k=1}^{K} \cos(\omega_k \odot g(\hat{\mathcal{D}}_i^s), \omega_k \odot g(\hat{\mathcal{D}}_j^s)) \]

Here \( K \) is the number of heads, and \( \omega_k \) are learnable weights emphasizing meaningful feature dimensions. The result is a structured matrix capturing inter-task relationships.

2. Enforcing Relation-Aware Regularization

Given \( \mathcal{M} \), the model adds a relation-aware consistency regularization term \( \mathcal{L}_{TR} \) to its learning objective:

\[ \mathcal{L}_{TR}(\hat{\mathcal{D}}_{i}^{q}, f_{\theta}^{i}) = \frac{1}{N_{i}^{q}} \sum_{j=1}^{N_{i}^{q}} \ell\left(\frac{\sum_{p \neq i} m_{ip} f_{\theta}^{p}(x_{ij})}{\sum_{q \neq i} m_{iq}}, y_{i,j}\right) \]

This term enforces that predictions for task \( \tau_i \) align with those from similar tasks, weighted by their similarity scores. The meta-learning objective becomes:

\[ \arg\min_{\mathcal{F}_{\theta}} \frac{1}{N_{tr}} \sum_{i=1}^{N_{tr}} \big[ \mathcal{L}(\hat{\mathcal{D}}_{i}^{q}, f_{\theta}^{i}) + \lambda \mathcal{L}_{TR}(\hat{\mathcal{D}}_{i}^{q}, f_{\theta}^{i}) \big] \]

The parameter \( \lambda \) balances standard learning with relation-aware consistency. This loss encourages the model to extract robust, shared features, mitigating underfitting and overfitting alike.

Experimental Validation: TRLearner in Action

The authors tested TRLearner across an extensive range of benchmarks—regression, image classification, drug activity prediction, and pose estimation—using multiple baseline algorithms (MAML, ProtoNet, ANIL, T-NET, and MetaSGD).

Regression

On Sinusoid and Harmonic regression tasks, TRLearner substantially reduces Mean Squared Error (MSE). For example, in 5-shot learning, MAML+TRLearner lowers the MSE from 0.593 to 0.400.

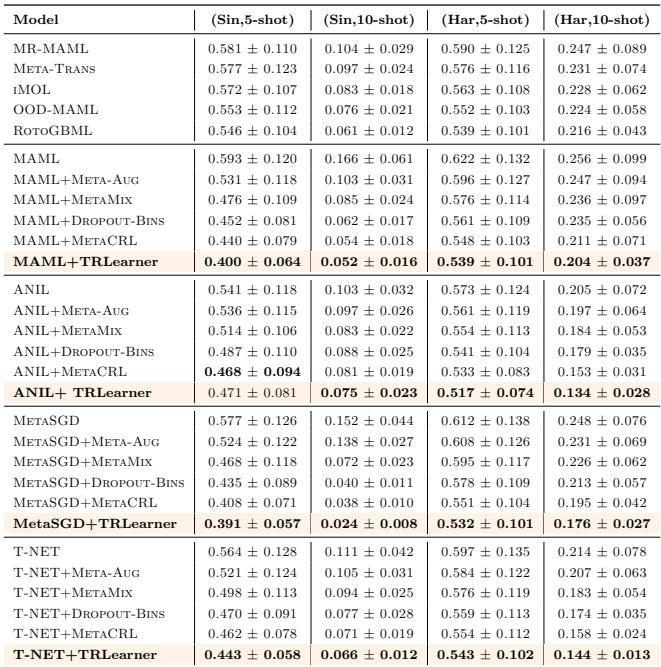
Table showing MSE results for regression.

“Comparison of MSE for regression tasks. TRLearner consistently yields the best results (highlighted in orange).”

Image Classification

In standard few-shot learning (SFSL) on miniImageNet and Omniglot, and cross-domain few-shot learning (CFSL) on miniImageNet→CUB and Places, TRLearner improves accuracy across baselines.

Table showing image classification accuracy.

“TRLearner improves accuracy across multiple few-shot and cross-domain settings.”

Drug Activity and Pose Prediction

On complex domains like pQSAR drug profiling and Pascal 3D pose estimation, TRLearner matches or exceeds all state-of-the-art baselines—demonstrating that its relational calibration generalizes beyond image tasks.

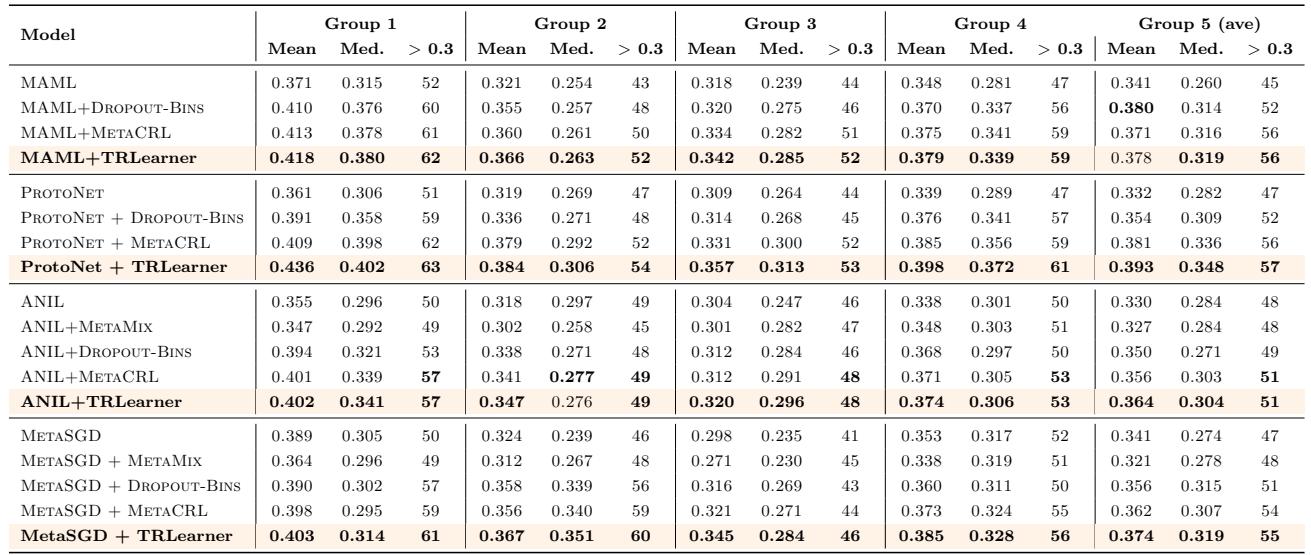
Table showing performance on drug activity prediction.

“Performance on drug activity prediction. TRLearner delivers the highest mean and median reliability scores.”

Out-of-Distribution (OOD) Generalization

Evaluated on the Meta-Dataset benchmark (10 distinct catalogs spanning visual domains), TRLearner exhibits remarkable OOD enhancement. For MAML, overall accuracy jumps from 24.5% to 33.0%, while OOD accuracy rises from 19.2% to 29.5%.

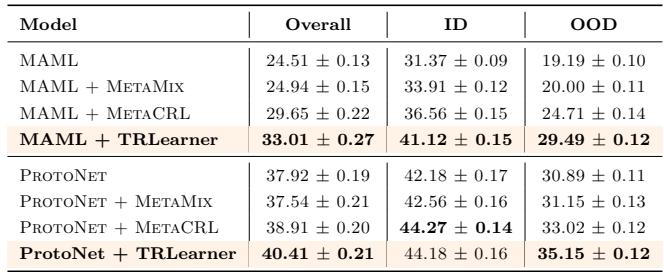
Table showing OOD generalization results.

“Out-of-domain generalization improvement on Meta-Dataset. TRLearner delivers consistent gains.”

Why TRLearner Works: Insights and Visualizations

The paper’s ablation studies illuminate how TRLearner fixes core limitations of standard meta-learning and where its gains come from.

1. It Resolves Overfitting and Underfitting: Repeating the initial motivating experiment with TRLearner yields smoother, higher performance curves across all task complexities.

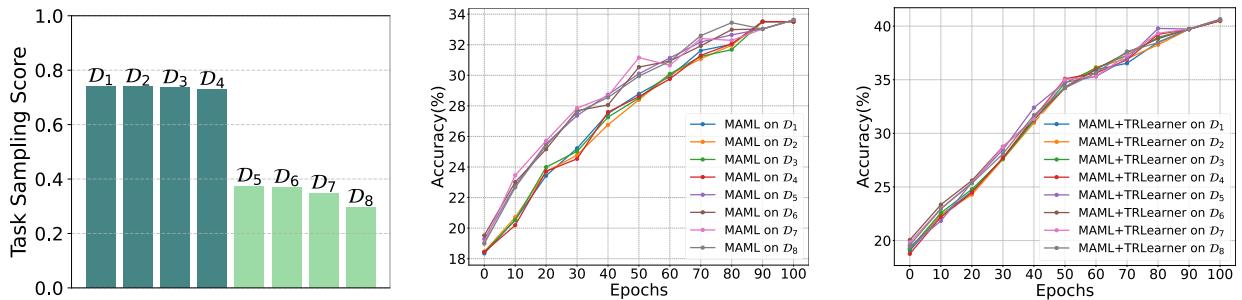
A three-panel figure showing task performance before and after TRLearner.

“Introducing TRLearner stabilizes MAML’s learning behavior and improves overall accuracy.”

2. It Reduces Modeling Dependence on Meta-Layers: Without TRLearner, performance increases only with more meta-layers. With TRLearner, a single meta-layer achieves competitive accuracy, and deeper setups maintain consistent results.

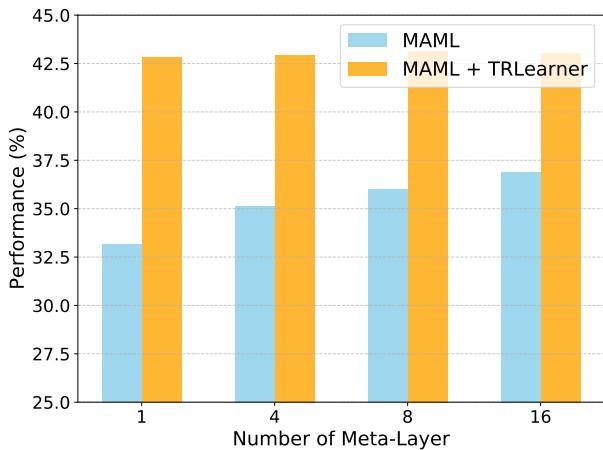
Bar chart illustrating meta-layer performance.

“TRLearner mitigates modeling errors—achieving high stability regardless of meta-layer depth.”

3. Relations Are Meaningful: Visualizations of learned task similarity matrices reveal more structured, discriminative relationships when TRLearner’s multi-headed similarity layer is used.

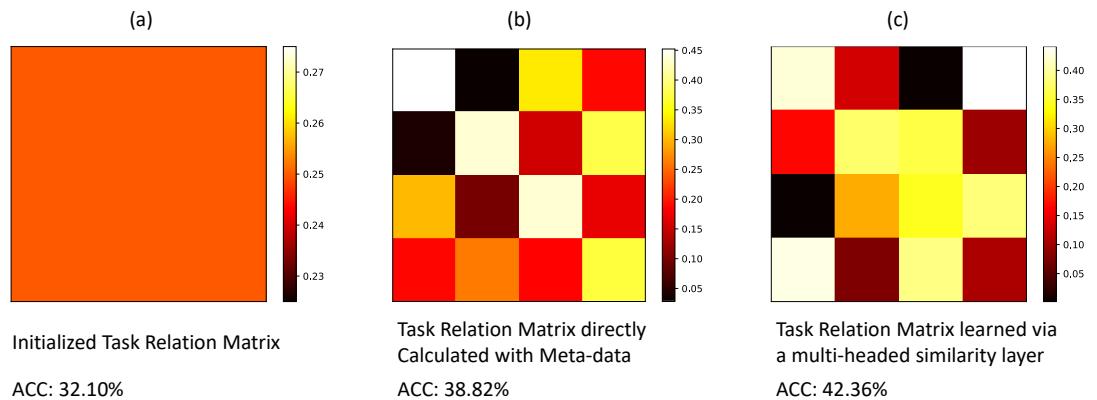
Three heatmaps of the task relation matrix.

“Learned task relation matrix (c) shows clearer patterns and leads to better model accuracy.”

4. Efficient Trade-Off: Despite slightly longer training time, TRLearner provides the best accuracy-to-cost ratio compared to other regularization methods.

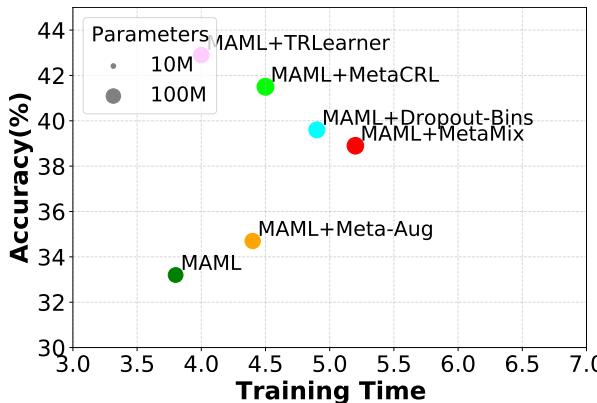
Trade-off scatter plot comparing accuracy vs training time.

“TRLearner offers the best trade-off with significant accuracy improvements under comparable runtime.”

From Theory to Practice: Why It Matters

Meta-learning’s philosophical promise has always been to learn how to learn. This paper reaffirms that by showing how learning itself can be improved not by adding parameters or data, but by letting tasks learn from each other.

The lessons are clear:

  1. The “One-Step” Rule is Fragile: Relying on a single gradient step makes models prone to underfitting or overfitting depending on task complexity.
  2. The Learning Lens Adds Flexibility: Modeling the meta-learner as a function that outputs task-specific models allows better theoretical alignment and adaptability.
  3. Task Relations Are Powerful Signals: Relating tasks through TRLearner’s similarity matrix helps focus learning on transferable, generalizable features.
  4. Consistency Drives Generalization: TRLearner’s regularization ensures similar tasks yield similar outputs, promoting robustness across domains.

Closing Thoughts

TRLearner is more than a technical improvement—it represents a conceptual evolution in how we approach meta-learning. Instead of treating tasks as independent examples, it views them as interconnected entities within a structured ecosystem of knowledge. This shift from learning in isolation to learning in relation could define the next generation of adaptive machine learning systems.

By learning not just how to learn, but how to relate, we unlock the potential for models that adapt faster, generalize better, and truly understand the tasks they face.