The Superposition Squeeze: How Many Features Can a Neuron Really Compute?

Modern AI models like Claude 3 Sonnet are linguistic wizards—but beneath the surface lies a fascinating mystery. Researchers at Anthropic recently uncovered about twelve million distinct, human-interpretable “features” within this model. A feature could be a concept as concrete as the “Golden Gate Bridge” or as abstract as “code written in Python.” The baffling part? The model has far fewer neurons than features.

This phenomenon, where a neural network represents far more features than it has neurons, is called superposition. It’s a key ingredient in the efficiency of large models, allowing them to pack vast amounts of knowledge into a relatively compact space. But it also throws a wrench into our efforts to understand how these models work—a field known as mechanistic interpretability.

Until now, most research has focused on how models represent or store features in superposition. But a critical question remained unanswered: what are the physical limits of actually computing with these compressed features? A recent paper from MIT, On the Complexity of Neural Computation in Superposition, tackles this head-on. Moving beyond representation, it establishes the first-ever theoretical speed limits for computation in superposition, revealing a striking gap between what neural networks can store and what they can compute.

Understanding Superposition

Before diving into the paper’s findings, let’s clarify the key ideas.

• Features: The atomic building blocks of neural representation. One feature might detect “cat ears,” another “pointy shapes,” and a third “furry textures.” Together, they combine to represent the concept of “cat.”
• Monosemantic vs. Polysemantic Neurons: In a monosemantic representation, each neuron corresponds to a single feature—clean but inefficient. In reality, neurons are often polysemantic, serving multiple features.
• Superposition: When a model uses more features than neurons, neurons must represent multiple features at once. Each feature occupies a unique direction in the neuron activation space. As long as these feature vectors are nearly orthogonal, the network can separate them.
• Feature Sparsity: This entire mechanism relies on the assumption that only a small subset of features is active for any given input. Without sparsity, overlapping activations would produce uncontrollable noise.

Superposition allows models like Claude 3 to store millions of distinct features. However, representing features is not the same as computing with them. Storing compressed information is like keeping books in an archive; computation is more like retrieving several books simultaneously, interpreting their contents, and writing a new compressed summary. The latter turns out to be exponentially harder.

Part 1: The Lower Bound — The Hard Limits of Superposition

To establish what’s theoretically possible, the authors use a general framework known as parameter-driven algorithms.

Imagine a universal machine \(T\): given a set of parameters \(P\), it can perform any task from sorting numbers to detecting cats. The neural architecture itself is \(T\); the parameters (weights and biases) define which function the network performs. This means the complexity of computation depends on the length of those parameter descriptions.

Using an information-theoretic argument, the authors show that if a network must compute all possible permutations of \(m'\) items, its parameters need at least
\(\log_2(m'!) \approx m' \log m'\) bits. That’s because the parameters must uniquely identify each possible function. More generally, for a broad class of logical operations—including Neural Permutation and 2-AND (a set of pairwise Boolean ANDs)—the network must encode at least
\(\Omega(m' \log m')\) bits of information.

Assuming square weight matrices, this implies a lower bound of
\(\Omega(\sqrt{m' \log m'})\) neurons.

Key result: To compute \(m'\) features in superposition, you need at least \(\Omega(\sqrt{m' \log m'})\) neurons and \(\Omega(m' \log m')\) parameters.

This finding yields several crucial insights:

1. A Fundamental Cap on Computation: A layer with \(n\) neurons can compute at most \(O(n^2 / \log n)\) features in superposition. That’s the first subexponential cap ever proved for superposed computation.
2. Representation Versus Computation: Representing features can be exponentially more efficient than computing them. There’s an exponential gap between passive storage and active logic.
3. Limits on Compression: Techniques like quantization or pruning face a hard floor—compressing a network beyond these bounds necessarily sacrifices computational accuracy.

Part 2: The Upper Bound — Building an Efficient Superposed Computation

A lower bound tells us what we cannot do. An upper bound tells us what we can. The authors provide a constructive example: a provably correct neural network that computes multiple logical operations in superposition almost optimally, using only
\(O(\sqrt{m' \log m'})\) neurons.

Step 1: Compression and Decompression

The foundation is a pair of matrices—compression and decompression. These convert between sparse (monosemantic) representations and dense (superposed) ones.

• Compression: A sparse vector \(\mathbf{y} \in \{0,1\}^m\) is multiplied by a random matrix \(C \in \{0,1\}^{n \times m}\), producing a shorter, dense vector
  \(\mathbf{x} = C\mathbf{y}\).
• Decompression: Using a matrix \(D\), constructed by transposing and normalizing \(C\), we can approximately recover the original sparse vector:
  \(\hat{\mathbf{y}} = D\mathbf{x} = DC\mathbf{y} \approx \mathbf{y}\).

The matrix \(D\) reverses the compression, ensuring that sparse activations can be approximately recovered from dense representations.

Because features are sparse, the reconstructed vector remains accurate with high probability. This compression/decompression trick is the backbone of all subsequent constructions.

Step 2: Solving the Neural Permutation Problem

For a simpler warm-up, the researchers show how to compute a permutation entirely in superposition. Represent the permutation with a matrix \(P\). Then define one transformation matrix:

Applying this to the compressed input \(\mathbf{x} = C\mathbf{y}\) yields \(T\mathbf{x} \approx C(P\mathbf{y})\), the correctly permuted output in superposed form. Small numerical errors can be cleaned up using a ReLU-based thresholding step.

This demonstrates that logical operations can be done without decompressing the inputs into their full dimension—a first hint that computation in superposition is feasible.

Step 3: Computing 2-AND in Superposition

The heart of the paper lies in computing pairwise ANDs across many features simultaneously—essentially, performing logical operations in compressed space.

The algorithm hinges on dividing the problem into subcases based on a new metric: feature influence, meaning how many outputs an input participates in.

• Light inputs: Influence ≤ \(m'^{1/4}\).
• Heavy inputs: Influence > \(m'^{1/4}\).
• Outputs: Labeled double-light, double-heavy, or mixed depending on which inputs they combine.

Each category uses a specialized strategy. All follow a shared architecture of compression–computation–decompression blocks.

Independent matrix partitions allow each subproblem to be computed without interference, ensuring clean logical results.

Case 1: Double-Light Outputs

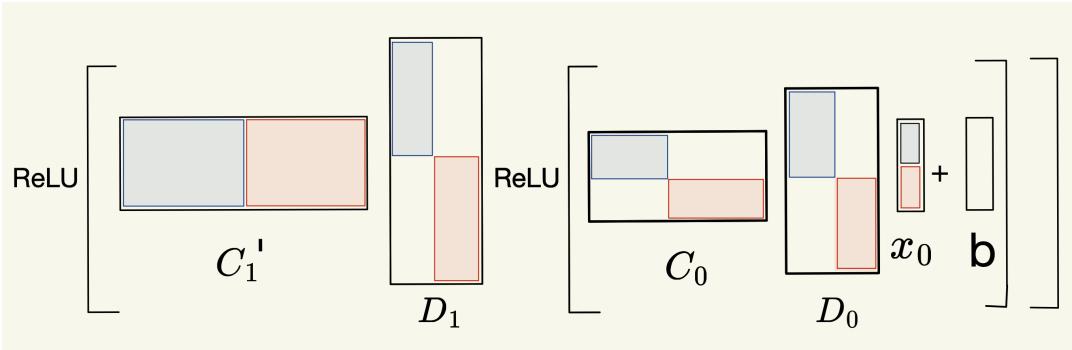
When all inputs are light, the algorithm uses output channels—dedicating a random binary vector \(s_i\) to each output feature. Inputs participating in output \(i\) share the same “channel” vector.

Each output channel routes the correct input pairs through aligned columns of \(C_0\) and corresponding rows of \(D_1\).

Here’s the simplified flow:

1. Recover an approximate sparse input \(\hat{\mathbf{y}}\) using \(D_0x_0\).
2. Multiply by \(C_0\) so that each pair of relevant inputs overlap in shared channel positions.
3. Subtract a bias of -1, then apply ReLU—this keeps only the activations where both inputs were 1.
4. Decompress and recompress to clean up noise and re-enter superposed space.

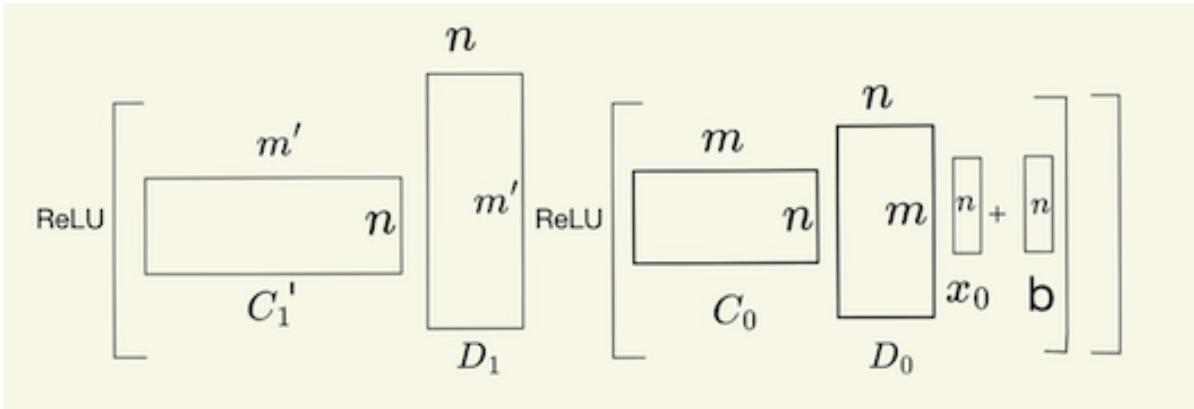
The 2-AND computation proceeds through successive compression/decompression and ReLU stages, enabling logical computation in compressed space.

This method works efficiently, achieving the desired neuron bound while keeping noise manageable via thresholding steps.

Case 2: Heavy and Mixed Outputs

For higher-influence features, the paper introduces input channels, where each high-influence input gets its own random encoding, and hybrid schemes that combine input and output channels depending on influence levels.

Mixed cases—one light and one heavy input—require additional mechanisms to prevent cross-channel interference. The most complex involves detecting when two “super heavy” inputs are active simultaneously and automatically canceling their combined outputs to preserve correctness.

Despite their intricacy, all versions achieve the same asymptotic efficiency:

Implications and Broader Significance

The paper’s contributions mark a turning point for both theory and interpretability.

1. A Fundamental Limit on Neural Efficiency: A network layer with \(n\) neurons can compute only \(O(n^2 / \log n)\) features. This defines a ceiling for compact computation.
2. An Exponential Gap Between Representation and Computation: It’s far easier for neurons to store features than to actively compute with them. Superposition helps with memory, not logic.
3. Blueprints for Mechanistic Interpretability: These explicit algorithms—especially the “output channel” technique—mirror behaviors found in trained networks. They provide theoretical scaffolding for interpreting learned circuits.
4. New Ground for Complexity Theory in AI: The work bridges classical complexity concepts (like Kolmogorov and information bounds) with modern neural computation, paving the way for a unified theory of efficiency and interpretability.

The researchers conclude with open questions: Can these theoretical bounds be applied directly to large language models? Can explicit superposed algorithms inspire new architecture designs that are both efficient and interpretable? And can feature influence become a measurable quantity guiding real-world model analysis?

As AI systems grow, understanding their fundamental computational limits will become vital—not just for efficiency, but for building models that are transparent, reliable, and safe.

In short: Superposition lets neural networks represent enormously more features than neurons—but when it comes to computing those features, reality sets in. You can’t cheat the math: even packed neurons have limits, and now we finally know where they are.