Introduction

In the quest to accelerate drug discovery and material science, generative Artificial Intelligence has emerged as a formidable tool. The dream is simple: instead of screening billions of existing molecules to find one that works, we ask an AI to design the perfect molecule from scratch—one that binds to a specific protein, has low toxicity, and is easy to synthesize.

However, the reality of 3D molecule generation is mathematically and computationally brutal. Molecules are not just strings of text (SMILES) or 2D drawings; they are dynamic 3D structures defined by quantum mechanics. To generate them, models must place atoms in precise 3D coordinates while adhering to strict physical laws and symmetries (such as rotation and translation).

Current state-of-the-art models, particularly Equivariant Diffusion Models (EDMs), treat molecules as “point clouds” of atoms. While effective, these models often struggle with the “curse of dimensionality.” They try to learn the complex distribution of atoms in high-dimensional space directly. This often results in unstable structures or molecules that fail to meet specific property constraints (conditional generation).

In this deep dive, we explore a new framework titled GeoRCG (Geometric-Representation-Conditioned Molecule Generation). The authors propose a clever divide-and-conquer strategy: instead of generating a molecule in one go, first generate a compressed, information-rich “representation” of the molecule, and then use that representation to guide the construction of the 3D structure.

This approach not only stabilizes generation but also yields a massive 50% improvement in conditional generation tasks. Let’s unpack how it works.

Background: The Challenge of 3D Generation

To understand why GeoRCG is necessary, we must first understand how modern AI represents molecules.

Molecules as Point Clouds

In this domain, a molecule \(\mathcal{M}\) is defined by two matrices:

1. Coordinates (\(\mathbf{x}\)): An \(N \times 3\) matrix representing the 3D positions of \(N\) atoms.
2. Features (\(\mathbf{h}\)): An \(N \times d\) matrix representing atomic types (Carbon, Oxygen, etc.) and other properties.

The Symmetry Problem

If you rotate a molecule by 90 degrees, it remains the same molecule with the same chemical properties. This property is called SE(3) invariance (rotation and translation). Generative models must be “equivariant,” meaning if the input rotates, the output rotates accordingly, but the probability of the molecule existing remains constant.

Achieving this equivariance restricts the architecture of neural networks. Models like EDM use Equivariant Graph Neural Networks (EGNNs) to handle this. However, mapping random noise directly to a valid, high-quality equivariant molecule is difficult because the “manifold” (the subspace of valid molecules) is extremely thin compared to the vastness of 3D space.

The GeoRCG Framework

The core insight of GeoRCG is that we can simplify the problem by introducing an intermediate step. Molecules might be complex in 3D space, but they can be mapped to a lower-dimensional “latent space” or representation.

If we can first generate a meaningful representation (which is just a vector without complex symmetry requirements), we can use that vector to strictly guide the difficult 3D generation process.

The framework consists of two distinct stages, as illustrated below:

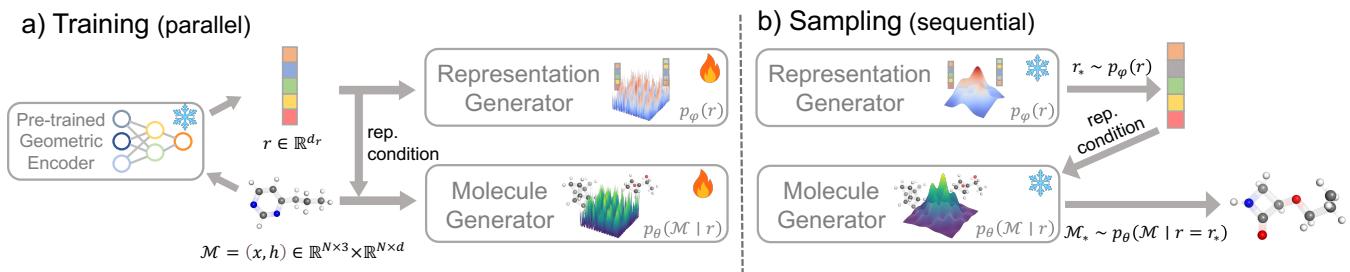
Stage 1: The Geometric Encoder and Representation Generator

The first step involves a “teacher” model. The authors utilize a pre-trained Geometric Encoder (\(E\)), such as Uni-Mol or Frad. These are powerful models pre-trained on massive molecular datasets to understand chemistry. When fed a molecule \(\mathcal{M}\), the encoder outputs a compact vector \(r\) (the representation).

This representation \(r\) encapsulates crucial info: atom counts, bond types, and global properties. Crucially, this vector space does not have rotation symmetries—it’s just a distribution of numbers.

The authors then train a lightweight Representation Generator (\(p_{\phi}(r)\)). This is a simple diffusion model (using standard MLPs) that learns to generate these representation vectors from scratch.

Why is this easier? Generating a vector \(r\) is a standard statistical problem. There are no 3D symmetries to worry about, and the dimensionality is lower. The loss function for this stage is a standard denoising objective:

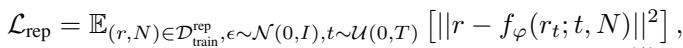
Here, the model tries to predict the clean representation \(r\) from a noisy version \(r_t\), conditioned on the number of atoms \(N\).

Stage 2: The Molecule Generator

Once we have a representation \(r\), we need to convert it back into a 3D molecule. This is where the Molecule Generator (\(p_{\theta}(\mathcal{M} | r)\)) comes in.

This generator is an equivariant diffusion model (like EDM). However, instead of generating from pure noise, it is conditioned on the representation \(r\) generated in Stage 1. The representation acts as a blueprint, telling the diffusion model exactly what kind of molecule to build (e.g., “build a stable ring structure with high polarity”).

The training objective for this stage ensures the model learns to reconstruct the molecule \(\mathcal{M}\) given its representation:

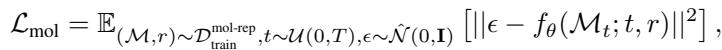
This decomposition allows the heavy lifting of understanding “what a molecule is” to be handled by the representation, while the “where atoms go” part is handled by the equivariant generator.

Why It Works: Theoretical Intuition

The authors provide a rigorous theoretical analysis proving that this two-stage approach reduces the error bound compared to single-stage methods.

In standard diffusion, the error comes from three sources:

1. Convergence: Does the noise turn into data?
2. Discretization: Errors from taking finite steps in the diffusion process.
3. Score Estimation: How accurately the neural network predicts the gradient (the score).

GeoRCG improves this by tightening the bounds on the score estimation. Because the second stage is conditioned on a highly informative vector \(r\), the uncertainty in the generation process drops significantly.

The equation above essentially states that the total error is bounded by the quality of the representation generation (Stage 1) plus the conditional generation error (Stage 2). Since \(r\) is easier to generate, and generating \(\mathcal{M}\) given \(r\) is easier than generating \(\mathcal{M}\) from nothing, the total error decreases.

Visualizing the Representations

To confirm that the representations are meaningful, the authors visualized them using t-SNE.

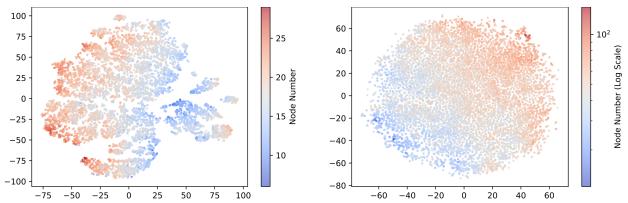
As seen in Figure 2, the representations naturally cluster by molecular size (node count). This structure makes it much easier for the Representation Generator to learn the distribution compared to the chaotic distribution of raw atom coordinates.

Conditional Generation: The “Killer App”

The most significant advantage of GeoRCG appears in conditional generation. In drug discovery, we don’t just want any molecule; we want a molecule with specific properties (e.g., a specific HOMO-LUMO gap energy).

In traditional models, you force the complex 3D generator to learn these property mappings directly. In GeoRCG, the workflow is elegant:

1. Train the lightweight Representation Generator to be conditional: \(p_{\phi}(r | c)\), where \(c\) is the property.
2. Keep the heavy Molecule Generator fixed.

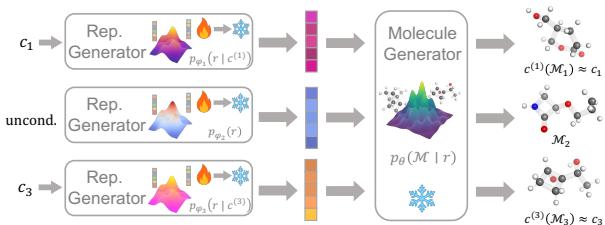
As shown in Figure 3, if you want to generate molecules for different properties (Condition 1, Condition 3), you only need to retrain or fine-tune the Representation Generator. The expensive Molecule Generator remains the same because it simply translates any representation into 3D coordinates.

Results on Conditional Tasks

The results on the QM9 dataset are striking. The authors compared GeoRCG against top baselines like EDM, EquiFM, and GeoLDM.

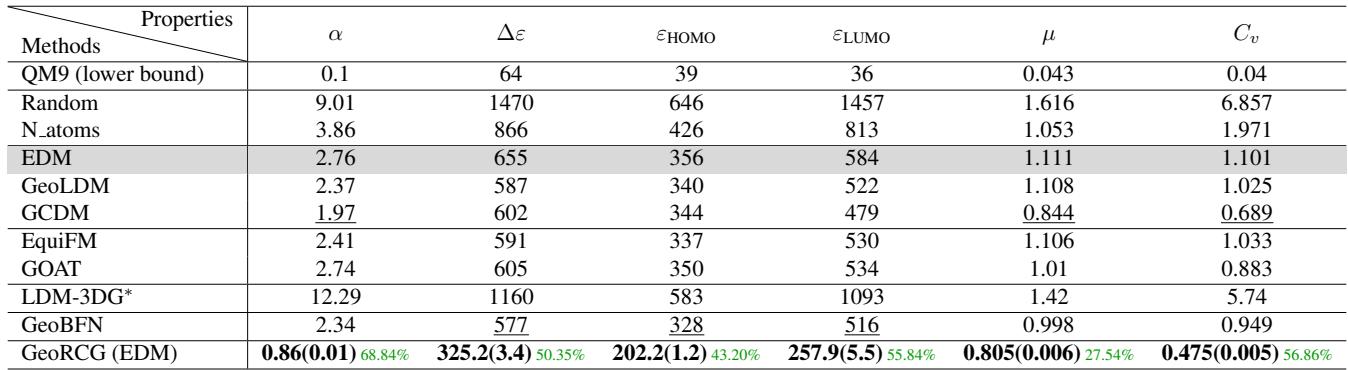
Look at the GeoRCG (EDM) row in Table 3. The metrics (Mean Squared Error between target and actual properties) are significantly lower.

• Polarizability (\(\alpha\)): Error reduced from ~2.4 (EquiFM) to 0.86.
• Gap (\(\Delta \epsilon\)): Error reduced from ~590 to 325.

This represents roughly a 50% improvement over state-of-the-art methods. The model is exceptionally good at listening to the prompt.

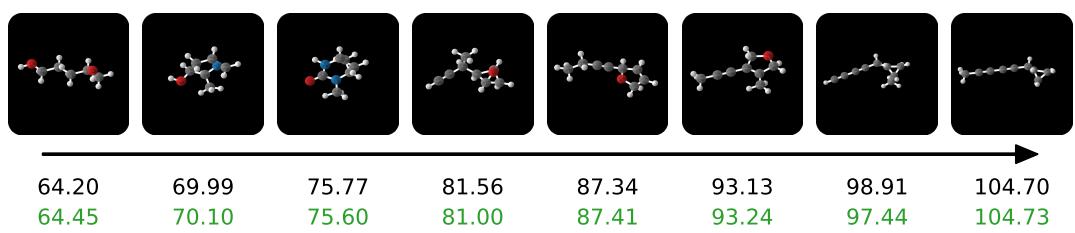
Below are samples generated conditioned on the polarizability property (\(\alpha\)). You can see the complexity of the molecules increasing as the target value (black number) increases.

Unconditional Generation & Efficiency

Even without specific conditions, GeoRCG produces higher quality molecules than its predecessors.

Quality Metrics

Using the QM9 and GEOM-DRUG datasets, the authors measured:

• Atom Stability: Are atoms forming the right number of bonds?
• Molecule Stability: Is the whole molecule stable?

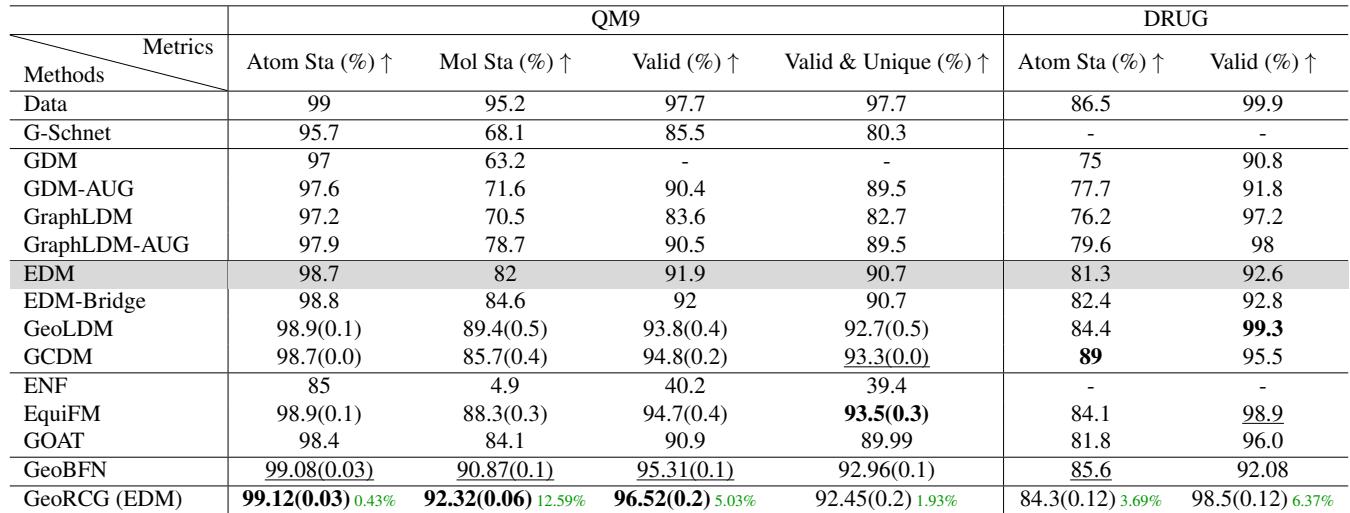
In Table 1, GeoRCG (built on top of EDM) boosts Molecule Stability on QM9 from 82% (EDM) to 92.32%. It even enhances the performance of the cutting-edge SemlaFlow model (see Table 2 below), proving that GeoRCG is a general framework that can upgrade various base generators.

Speed: Fewer Steps Required

Diffusion models are notoriously slow because they require iterative denoising (often 1000 steps). Because the geometric representation provides such a strong “hint” to the molecule generator, GeoRCG can generate high-quality samples in far fewer steps.

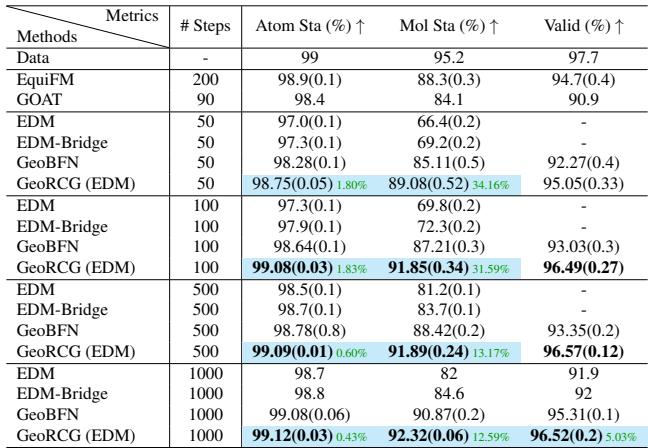
Table 4 shows that GeoRCG with only 100 steps achieves a molecule stability (91.85%) that rivals the best competitors running at 1000 steps. This 10x speedup is vital for high-throughput screening.

Balancing Quality and Diversity

In generative modeling, there is often a trade-off: do you want high-quality (stable) samples, or diverse samples? GeoRCG offers a “knob” to control this via Classifier-Free Guidance (CFG) on the representation.

By adjusting the guidance weight (\(w\)) and the sampling temperature (\(\tau\)), researchers can tune the model.

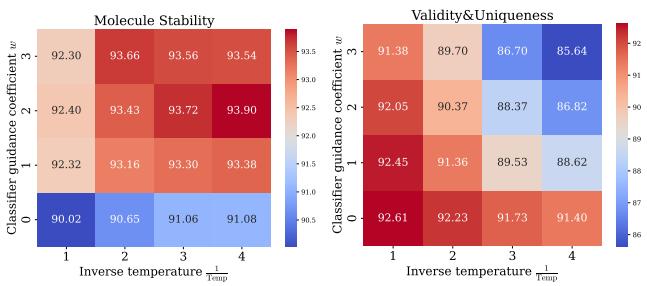
Figure 4 demonstrates that increasing guidance (\(w\)) improves stability (red areas in the left heatmap) at the cost of uniqueness (blue areas in the right heatmap). This gives researchers control depending on whether they are exploring new chemical spaces (high diversity) or optimizing a lead (high stability).

Conclusion

The GeoRCG paper identifies a bottleneck in 3D molecule generation: the immense complexity of directly modeling atomic coordinates in Euclidean space. By acknowledging that molecules are semantically defined by their properties and geometric encoding, the authors successfully decoupled the “what” (representation) from the “where” (coordinates).

Key Takeaways:

1. Two-Stage is Better: Generating a geometric representation first acts as a stable foundation for 3D construction.
2. SOTA Conditional Generation: A 50% reduction in error for property-constrained generation is a massive leap for drug discovery applications.
3. Efficiency: The method works well even with 90% fewer diffusion steps.
4. Generality: The framework improves both simple (EDM) and complex (SemlaFlow) base models.

This work paves the way for more controllable and reliable generative AI in chemistry, moving us one step closer to designing drugs on demand.

The images and data presented in this article are derived from the research paper “Geometric Representation Condition Improves Equivariant Molecule Generation” (2025).