Beyond 'Train as You Test': How Contrastive Learning Supercharges Meta-Learners

Humans have a remarkable ability to learn new skills from just a handful of examples. Show a child a picture of a zebra, and they can likely identify other zebras in different contexts—even if they’ve never seen one before. This stands in stark contrast to most deep learning models, which often require thousands or even millions of labeled examples to achieve similar accuracy.

This gap inspired a field of AI called meta-learning, or “learning to learn.” The goal of meta-learning is to build models that, like humans, can generalize from few examples and adapt quickly to new tasks. Traditional methods follow a simple rule: train as you test. They simulate learning on new, few-shot tasks during training so the system can learn a generalizable strategy.

But what if train as you test is too narrow? When a meta-learner trains on multiple tasks—say one about classifying dog breeds and another about recognizing car models—it learns each independently. The fact that these tasks are different provides valuable information that is usually ignored.

A recent paper, “Learning to Learn with Contrastive Meta-Objective” , proposes an elegant solution. The researchers introduce ConML, a framework that enhances meta-learning by training the model with two cognitive skills fundamental to human learning:

1. Alignment — The ability to recognize that different views or subsets of data for the same task should yield a similar understanding.
2. Discrimination — The ability to recognize that data from different tasks should lead to distinct models and representations.

By adding a contrastive objective that explicitly optimizes for these behaviors, ConML systematically improves a broad class of meta-learning algorithms. It’s small, efficient, and remarkably universal.

Let’s unpack how it works.

Meta-Learning Refresher

Imagine you want a classifier that can recognize any new group of animals after seeing just five examples per species—a typical few-shot learning problem.

Meta-learning doesn’t train one classifier directly. Instead, it trains a meta-learner: an algorithm that creates classifiers. The meta-learner is exposed to a range of tasks across domains—say, flower recognition, vehicle identification, and handwriting classification.

Each training episode consists of:

• A support set (small training set): e.g., 5 images per class.
• A query set (validation set): a few additional examples of the same classes.

The meta-learner uses the support set to build a task-specific model and is rewarded for how well that model performs on the query set. Training consists of many such “episodes” across different tasks. Over time, the meta-learner develops an internal strategy for fast adaptation—learning quickly from limited data.

ConML: Contrastive Learning in Model Space

Contrastive learning has revolutionized unsupervised representation learning. The principle: pull similar examples (“positive pairs”) closer together and push dissimilar ones (“negative pairs”) apart in representation space. ConML takes this philosophy further—it applies contrastive learning to the models themselves.

The insight is that the episodic meta-learning process naturally provides task identity. Each task comes with intrinsic supervision information—whether two datasets belong to the same or different tasks.

ConML harnesses this through contrastive learning in the model space:

• Alignment (Positive pairs): Models learned from different subsets of the same task should be similar.
• Discrimination (Negative pairs): Models learned from different tasks should be distinct.

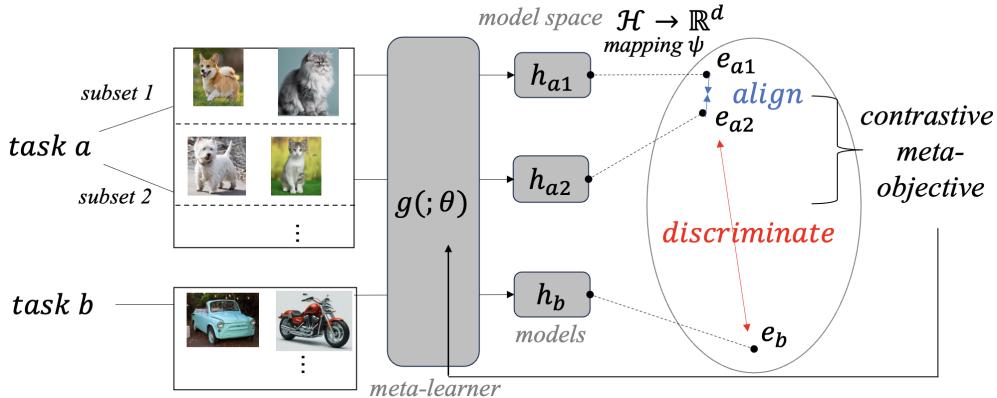
Figure 1: ConML performs contrastive learning on model representations—aligning similar task subsets while discriminating different tasks.

This approach makes task identity a source of additional supervision. The result: meta-learners become more robust to noisy subsets (through alignment) and generalize better to new tasks (through discrimination).

Building the ConML Framework

Step 1. Represent the Model

To compare two models, ConML introduces a projection function \( \psi \) that maps a trained model \( h = g(\mathcal{D}; \theta) \) into a fixed-length vector representation \( e = \psi(h) \). This step ensures compatibility with any meta-learner architecture—it’s what makes ConML learner-agnostic.

Step 2. Measure the Contrastive Objective

Each episode involves two types of distances:

• Inner-Task Distance (Alignment): Measure how consistent a meta-learner’s outputs are when trained on different subsets of the same task’s data. Minimizing this ensures coherent understanding within a task.

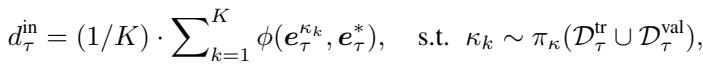
• Inter-Task Distance (Discrimination): Measure how distinct the outputs are for entirely different tasks. Maximizing this ensures models are not conflated across tasks.

Step 3. Combine the Losses

The contrastive objective \( \mathcal{L}_c = d^{in} - d^{out} \) is combined with the standard episodic loss \( \mathcal{L}_e \) (computed on query sets). A scalar \( \lambda \) balances the two:

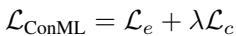
Equation: The ConML meta-objective combines learning-to-learn accuracy and contrastive regularization.

This computation is added seamlessly to the episodic training loop—incurring only minimal extra cost.

Algorithm: ConML-enhanced episodic training adds a few lightweight contrastive steps to standard meta-learning.

Integrating ConML Across Meta-Learning Categories

The mapping function \( \psi \) is defined differently depending on how the meta-learner models a task.

Table 1: Customizing the model representation \( \psi(g(\mathcal{D}; \theta)) \) for various meta-learning paradigms.

1. Optimization-Based (e.g., MAML): The model representation is the updated weights after gradient steps on the task data.

2. Metric-Based (e.g., ProtoNet): Represent each task by concatenating its class prototypes (means of the class embeddings).

3. Amortization-Based (e.g., CNAPs): The hypernetwork’s output—task-specific parameters—is used directly as the representation.

4. In-Context Learning (ICL): Large language models can perform meta-learning implicitly via prompts. To compute their “learned representation,” ConML introduces a dummy probe input \( u \) (e.g., “what is this task?”). The model’s output for this input becomes its representation.

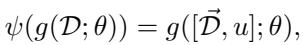
Equation: Obtaining model representations in in-context learning via probing.

This flexibility enables ConML to plug into nearly any meta-learning or in-context learning system.

Experiments: Universal Gains in Performance

Few-Shot Image Classification

The authors tested ConML across multiple meta-learning algorithms—optimization-, metric-, amortization-, and in-context-based—on miniImageNet and tieredImageNet benchmarks.

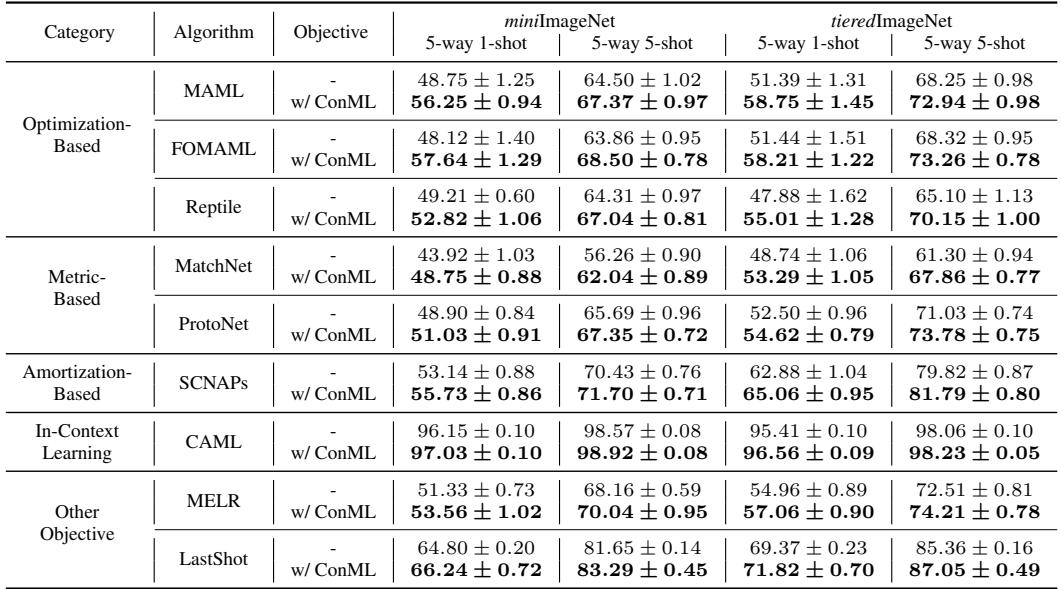
Table 2: ConML consistently improves the performance of diverse meta-learning algorithms on classic few-shot benchmarks.

Even without fine-tuning hyperparameters, ConML boosted accuracy by several percentage points for every learner type.

To test generalizability, they evaluated on META-DATASET, a complex benchmark spanning multiple image domains.

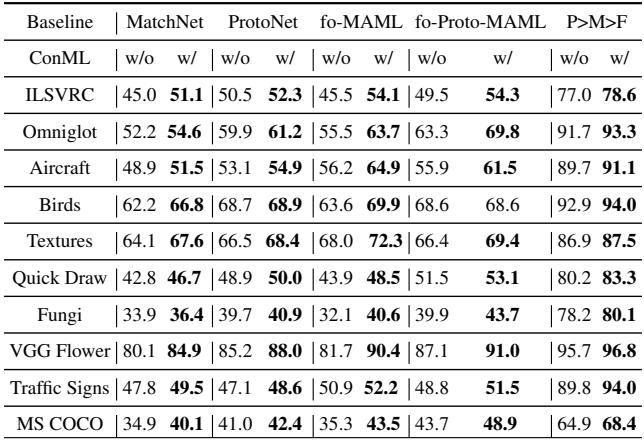
Table 3: ConML improves cross-domain generalization, showing its problem-agnostic nature.

The improvements held across radically different datasets, confirming ConML’s versatility.

In-Context Learning: Smarter Transformers

ConML was also applied to in-context learning. The researchers trained GPT-2–like transformers on synthetic function classes—linear regression (LR), sparse regression (SLR), decision trees (DT), and small neural networks (NN).

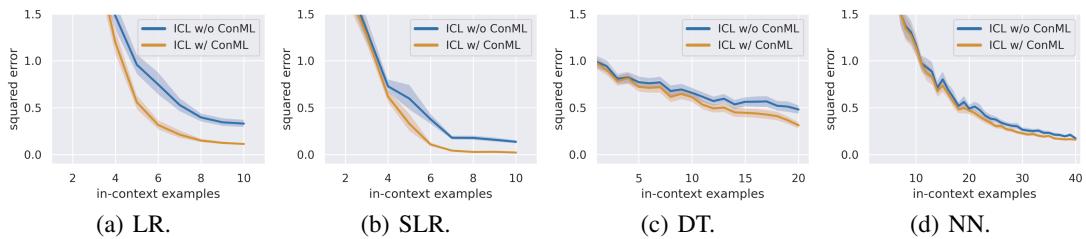
Figure 3: ICL with ConML consistently yields lower inference errors across various problem types.

In every scenario, ICL+ConML models achieved the same accuracy as standard ICL using fewer examples in the prompt—often saving 4–5 shots.

Table 5: Quantitative advantages—lower relative error and fewer required examples for equivalent accuracy.

This result is especially compelling because ConML introduces no architectural change—just a training strategy that improves how the model learns from prompts.

Synthetic Analysis: Why ConML Works

To see why ConML improves learning, the team trained MAML on synthetic sine-wave regression tasks.

Visualizing model representations revealed the magic:

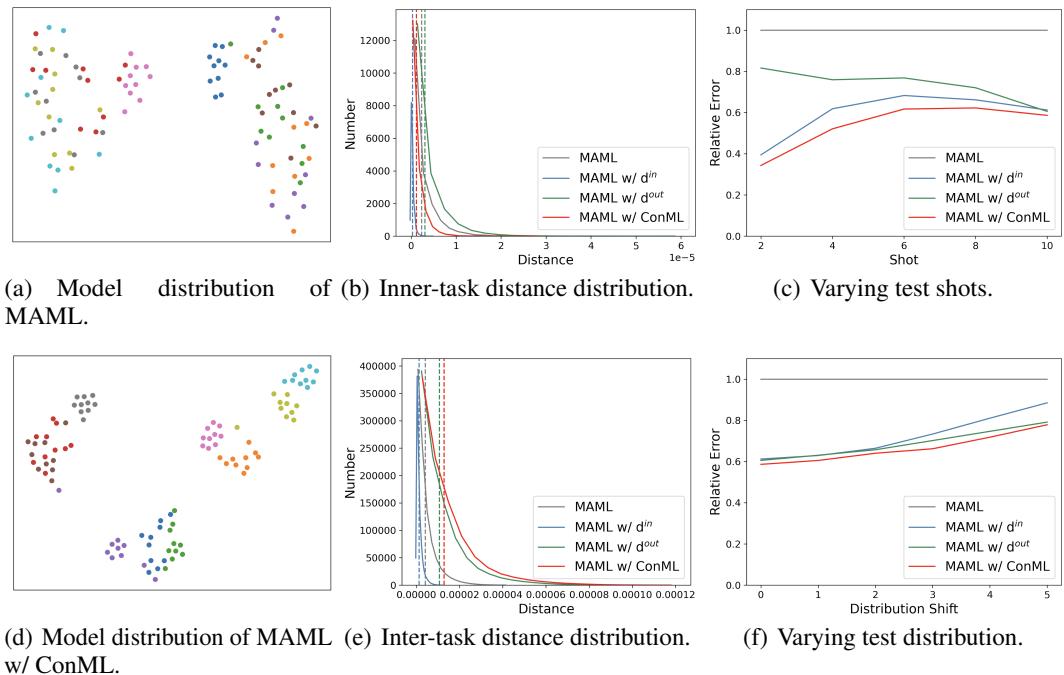
Figure 4: ConML enforces alignment and discrimination at the model level—tight clusters per task and clear separation between tasks.

Models from subsets of the same task clustered tightly (alignment), while different tasks remained well-separated (discrimination).

Further experiments showed:

• Alignment (minimizing \(d^{in}\)) improves fast adaptation—crucial for very few-shot settings.
• Discrimination (maximizing \(d^{out}\)) enhances task-level generalization—helping across domains or unseen distributions.

Even the simplest configuration with one subset sample (\(K=1\)) yields strong results at little computational cost.

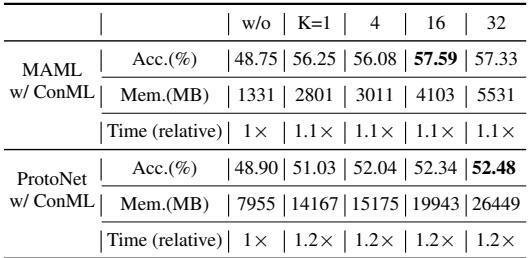
Table 4: ConML delivers large improvements with minimal resource overhead.

Conclusion

The paper “Learning to Learn with Contrastive Meta-Objective” introduces a simple yet transformative idea: task identity itself can serve as rich supervision for meta-learning.

By extending contrastive learning from representations in data space to representations of models in model space, ConML provides a universal way to enhance learning-to-learn.

Key Takeaways:

1. Human-Like Learning Objective: ConML teaches models to align similar views and discriminate among tasks—mirroring human learning.
2. Universal Applicability: It works with diverse meta-learning strategies and improves generalization across domains.
3. Efficient Implementation: A lightweight addition to existing meta-training loops that yields consistent gains.

ConML doesn’t replace existing meta-learning algorithms—it amplifies them. As AI progresses toward systems that learn dynamically from minimal data, ConML stands out as a principled and practical step in building more generalizable, adaptable learners.