Introduction: The Thirst for Data and the Promise of Learning to Learn

Deep learning has revolutionized fields from computer vision to natural language processing, but this success comes at a cost. State-of-the-art models are notoriously data-hungry, often requiring millions of labeled examples and immense computational power to train. But what if a model could learn a new skill from just a handful of examples, much like a human can? This is the central challenge of few-shot learning.

To tackle this, researchers have turned to meta-learning, a paradigm often described as “learning to learn.” Instead of training a model to master a single task, meta-learning trains a model on a wide variety of tasks, teaching it how to adapt quickly to new, unseen challenges with minimal data.

One of the most influential algorithms in this space is Model-Agnostic Meta-Learning (MAML). Its elegance lies in its simplicity: MAML learns an excellent initialization—an ideal starting point for any new learning task. From this initialization, a model can be fine-tuned for a new task using just a few gradient descent steps.

However, MAML has drawbacks. Its reliance on two nested loops of gradient descent—an inner loop for task-specific adaptation and an outer loop for meta-optimization—can be computationally expensive and slow. Furthermore, when training tasks differ significantly, MAML’s meta-updates can become unstable, as conflicting objectives pull the model in different directions.

This is where the recent paper, Fast Adaptation with Kernel and Gradient Based Meta Learning, makes its mark. It proposes a powerful two-part framework called Adaptive Meta-Learning in Functional Space (AMFS) that redefines both the inner and outer loops. The result is an approach that’s faster, more stable, and theoretically rich. Let’s explore how AMFS achieves this.

Background: Understanding MAML and Its Challenges

Before diving into AMFS, let’s unpack how MAML works. Imagine you want to train a model that can recognize bird species—but for any new species, you’ll only ever have five pictures.

MAML tackles this problem using a training process called episodic learning, where each episode simulates a mini “task.”

  1. Inner Loop (Task Adaptation): For each task, MAML starts with its current set of meta-parameters \(\theta\). It performs a few gradient descent steps on a small set of examples (the support set), yielding task-specific parameters \(\theta'\). This adaptation is quick but iterative.

  2. Outer Loop (Meta-Optimization): Once adaptation is complete, the model is tested on new examples from the same task (the query set). The resulting error informs an update to the original meta-parameters \(\theta\). Over many tasks, these updates help MAML learn an initialization that can adapt quickly to unseen data.

This elegant framework allows MAML to find a “sweet spot” in parameter space—a region from which adaptation to new tasks is fast and efficient.

But there are two critical issues:

  • Computational Cost: Every task requires multiple gradient steps, which becomes expensive for large models or datasets.
  • Instability: Summing gradients from very different tasks can lead to conflicting updates. The model might be pulled in opposing directions, hurting convergence and stability.

AMFS directly addresses these issues, introducing two enhancements—one for each loop.

The AMFS Framework: Redefining Speed and Stability

The Adaptive Meta-Learning in Functional Space (AMFS) framework combines two innovations:

  1. I-AMFS (Inner-loop AMFS): Replaces the iterative gradient updates in MAML’s inner loop with a fast, closed-form solution using kernel methods.

  2. O-AMFS (Outer-loop AMFS): Redefines the outer loop by weighting task gradients based on their similarity, stabilizing updates across diverse tasks.

Together, these form a highly efficient, theoretically grounded meta-learning system.

I-AMFS: A Faster Inner Loop in Functional Space

The most radical change in AMFS is where learning happens. Rather than updating model parameters through iterative gradient descent, I-AMFS operates in functional space—focusing on finding the best function for each task instead of the best weight configuration.

This is done using the Radial Basis Function (RBF) kernel, a well-known similarity measure that captures how close two data points are.

The Radial Basis Function (RBF) kernel measures similarity based on distance between data points.

“Figure: The RBF kernel captures nonlinear relationships by measuring how similar two data points are in input space.”

Using this kernel, I-AMFS formulates task adaptation as a straightforward optimization problem solvable in closed form—requiring no iterative gradient steps.

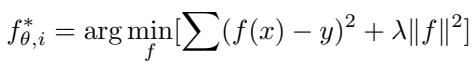
The optimization problem solved by I-AMFS balances data fitting with smoothness via a regularization term.

“Figure: I-AMFS minimizes training error while preventing over-complex functions using regularization.”

Thanks to the Representer Theorem, the optimal function can be expressed elegantly:

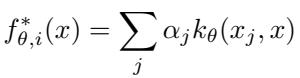
The closed-form solution expresses the function as a weighted sum of kernel similarities between input x and training examples.

“Figure: The adapted function is a weighted sum of kernel similarities, enabling fast, direct computation.”

The key coefficients (α) are calculated directly:

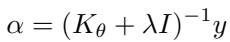
The equation to compute optimal weights α using the kernel matrix (K), regularization λ, and labels y.

“Figure: I-AMFS computes adaptation weights in one shot, replacing the multi-step gradients of MAML.”

Thus, the inner loop becomes a single matrix operation instead of multiple gradient updates—a dramatic speedup.

To ensure stability and generalization, I-AMFS introduces a refined objective function with additional regularization terms:

The full I-AMFS objective function includes task loss, gradient norm, and information-theoretic regularizers.

“Figure: The composite objective improves adaptation smoothness and information balance.”

Key Regularization Components:

  • Gradient Norm Regularization (\(\mu ||∇_f L_{T_i}||^2\)) Encourages smoother function adaptation, preventing overfitting and promoting generalization.

  • Information-Theoretic Regularization (\(\gamma I(f^*; D)\)) Limits how much training data the function can memorize, ensuring broader learning across tasks.

The kernel parameters themselves evolve during training, making the algorithm adaptable and flexible:

The meta-update rule for kernel parameters θ, optimized via gradient ∇θJ(θ).

“Figure: Kernel parameters are updated via meta-gradients, enabling adaptive similarity measurement.”

In short, I-AMFS compresses the entire inner loop into one efficient step, achieving both speed and stability. It trades iterative parameter tweaking for direct optimization in function space—a major conceptual and computational leap.

O-AMFS: Harmonizing the Outer Loop

Next, AMFS refines the outer loop, where MAML’s simple gradient aggregation can falter if task gradients conflict. O-AMFS tackles this by weighing each task’s gradient based on its similarity to others in the batch—introducing harmony in multi-task learning.

In standard MAML, the meta-update rule is:

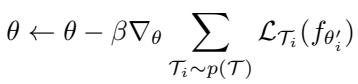
The standard MAML meta-update sums gradients from all tasks equally.

“Figure: Traditional MAML combines task gradients without considering their direction or relationship.”

O-AMFS modifies this by weighting task gradients according to cosine similarity—how parallel their update directions are.

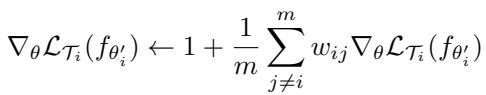
The O-AMFS weighted gradient update adjusts each task’s gradient based on its similarity to others.

“Figure: Gradients that agree are amplified, while conflicting ones are reduced.”

The similarity measure \(w_{ij}\) is computed as:

The formula for w_ij using cosine similarity between gradients of task i and j.

“Figure: Cosine similarity ensures that only directional agreement strengthens updates.”

This ensures that updates from aligned tasks reinforce each other, while outlier tasks have reduced impact.

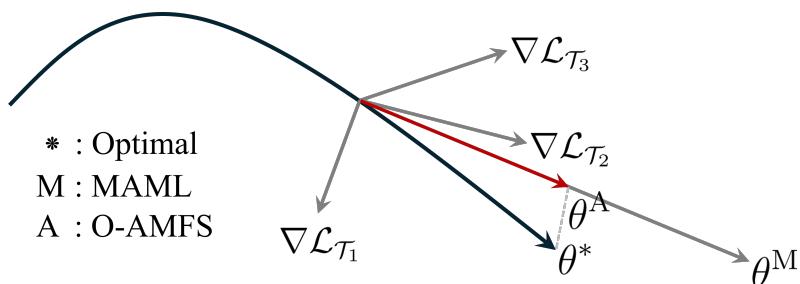
A schematic showing how O-AMFS directs updates toward an optimal point by considering task gradient similarity.

“Figure 1: O-AMFS keeps meta-updates closer to the optimal path (θ*), avoiding conflicting gradient directions.”

O-AMFS therefore creates a more unified learning trajectory—maintaining stability, improving convergence, and making the meta-learner more robust to diverse task distributions.

Experiments and Results: Putting AMFS to the Test

The researchers validated AMFS across popular few-shot learning benchmarks including Omniglot, Mini-ImageNet, CUB, and FC-100, comparing performance directly against MAML.

Few-Shot Classification Accuracy

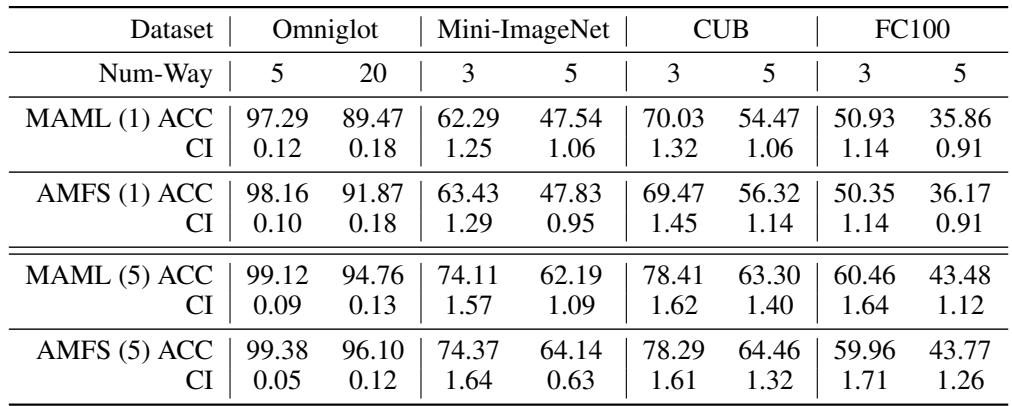
Table 1: Few-shot classification accuracy of AMFS versus MAML across multiple datasets. AMFS shows consistent gains and stable performance.

“Table 1: AMFS outperforms or matches MAML across datasets and task difficulties, confirming its efficiency and stability.”

Across all settings, AMFS demonstrates modest but consistent performance gains while reducing computational overhead—a testament to its more efficient optimization.

The Need for Speed: Fast Convergence

One of AMFS’s biggest advantages is its inner-loop efficiency. The authors compared how MAML accuracy scales with the number of gradient steps versus the fixed single-step I-AMFS.

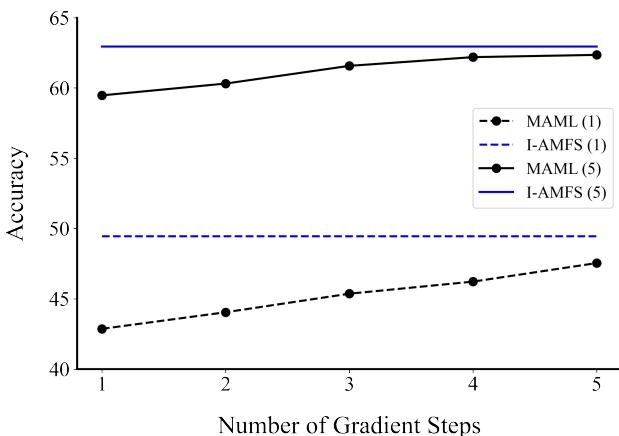
Figure 2: Comparison of MAML’s multi-step inner loop and I-AMFS’s one-shot adaptation. I-AMFS achieves high accuracy instantly.

“Figure 2: I-AMFS reaches near-optimal accuracy in one computation step, while MAML requires multiple gradient updates.”

The results show that I-AMFS achieves nearly the same accuracy as five-step MAML—in a single, non-iterative calculation. This means faster training and instant task adaptation at inference time.

Generalization Across Domains

Meta-learning’s ultimate goal is robust generalization to unseen tasks or domains. To test this, the authors evaluated AMFS in two scenarios:

  1. General → Specific (G → S): Train on Mini-ImageNet, test on CUB (bird images).
  2. Specific → General (S → G): Train on CUB, test on Mini-ImageNet.

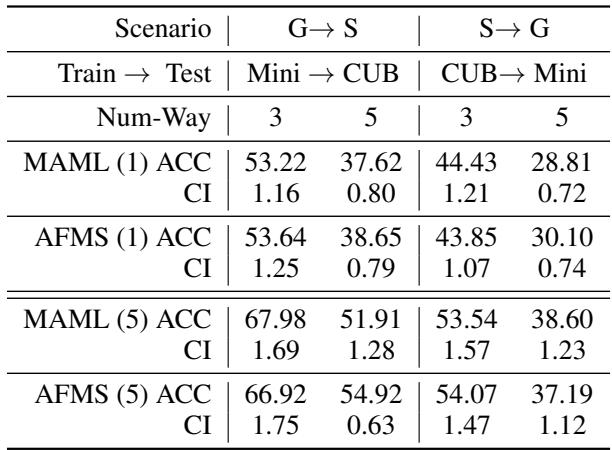
Table 2: Cross-domain generalization results. AMFS shows strong transfer in both directions compared to MAML.

“Table 2: AMFS maintains strong accuracy across domain shifts, indicating improved out-of-distribution generalization.”

AMFS maintains stable performance under significant distribution shifts, confirming the framework’s theoretical promise in robust domain adaptation.

Resilience to First-Order Approximation

Speed-focused alternatives to MAML, such as First-Order MAML (FO-MAML), drop second-order derivatives to save computation but at the cost of accuracy. The authors tested how AMFS behaves under this same simplification.

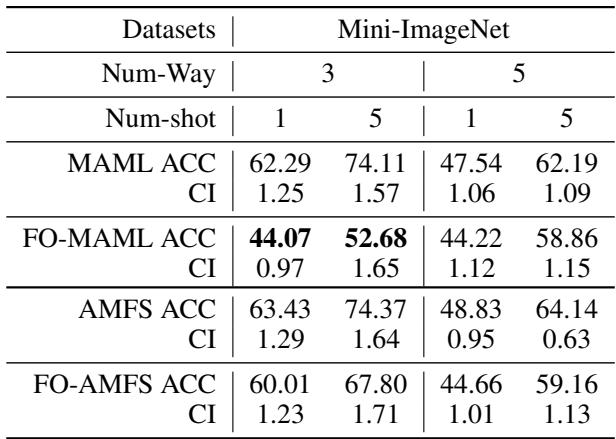
Table 4: MAML vs. AMFS under First-Order approximation. AMFS shows far smaller performance degradation.

“Table 4: AMFS sustains strong performance even under First-Order simplifications, thanks to its gradient weighting mechanism.”

AMFS remains stable and accurate even without second-order gradients, demonstrating an intrinsic robustness to noisy or approximate optimization.

Conclusion: Toward Practical Meta-Learning

The paper Fast Adaptation with Kernel and Gradient Based Meta Learning delivers a fresh take on model-agnostic meta-learning. Its two components—I-AMFS and O-AMFS—jointly solve MAML’s biggest challenges:

  • Speed and Efficiency (I-AMFS): Task adaptation is now a one-shot kernel-based operation, eliminating expensive gradient iterations.

  • Stability and Harmony (O-AMFS): Weighted gradient aggregation smooths out task inconsistencies and guides the meta-update toward more consistent improvements.

Together, these enhancements make AMFS not just faster, but more theoretically elegant and practically applicable.

As deep learning models continue to grow in size and complexity, the need for agile, efficient learning paradigms becomes ever more vital. AMFS brings us closer to the original vision of meta-learning—creating AI systems that can learn to learn quickly, with minimal data and maximal adaptability.

This work is more than a technical advancement—it’s a philosophical step toward the ideal of intelligent efficiency in machine learning.