Imagine teaching a brilliant student a new subject, only to find they’ve completely forgotten everything you taught them last week. This frustrating phenomenon—known as catastrophic forgetting—is one of the biggest challenges in artificial intelligence. As we deploy powerful models like Vision Transformers (ViTs), we want them to learn continuously from new data, mastering new tasks without requiring costly retraining from scratch. This is the central promise of Continual Learning (CL).

Traditional continual learning methods often rely on replaying old data, which isn’t always feasible due to storage, privacy, or compliance constraints. More recent approaches turn to Parameter-Efficient Fine-Tuning (PEFT), a strategy that adapts large models by tweaking only a small fraction of their parameters. Among these methods, Low-Rank Adaptation (LoRA) has emerged as particularly promising. However, applying LoRA directly to continual learning has been challenging—often leading to slower training and suboptimal retention of earlier knowledge.

A recent paper, Replay-Free Continual Low-Rank Adaptation with Dynamic Memory, introduces DualLoRA, a method that enables ViTs to learn a sequence of tasks efficiently and effectively, drastically reducing catastrophic forgetting. It achieves this through a clever dual-adapter architecture and a dynamic memory system that intelligently adapts the model at inference time.

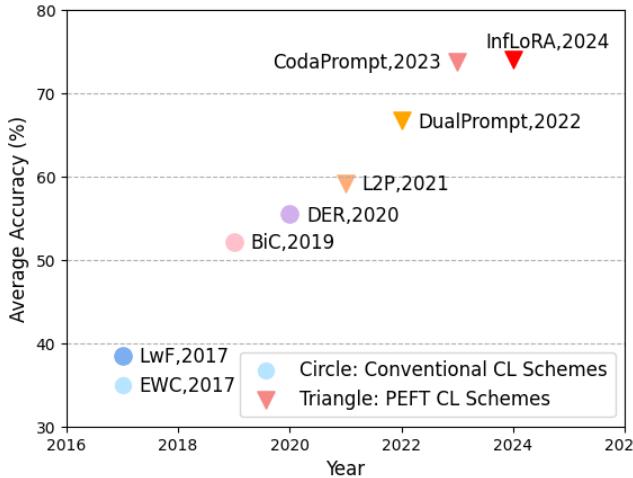
A chart showing the increasing accuracy of continual learning methods over the years, with PEFT-based methods like DualLoRA leading the pack.

Figure 1. Over the past decade, PEFT-based continual learning methods have steadily improved performance, culminating with DualLoRA as a new state-of-the-art.

Background: The Stability–Plasticity Dilemma

At the heart of continual learning lies a fundamental trade-off known as the stability–plasticity dilemma:

  • Stability: The model must retain knowledge from previous tasks.
  • Plasticity: It must remain flexible enough to learn new tasks.

Leaning too far in one direction breaks the balance—an overly stable model cannot adapt, while an overly plastic model forgets. The challenge is to maintain both in equilibrium.

Low-Rank Adaptation (LoRA)

LoRA fine-tunes models efficiently by freezing the vast pre-trained weights \( \mathbf{W}_0 \) and injecting small, trainable “adapter” matrices into each layer. Specifically:

\[ \mathbf{W} := \mathbf{W}_0 + \mathbf{B}\mathbf{A} \]

Here, \(\mathbf{B}\) and \(\mathbf{A}\) are low-rank matrices, and since the rank \(r \ll d\), only a small parameter subset is trained. This makes LoRA notably lightweight compared to full fine-tuning.

Gradient Projection: Learning Without Interference

To safeguard old knowledge, some continual learning methods use gradient projection. This technique identifies the “important” directions—subspaces critical for prior tasks—and constrains new gradients to be orthogonal to these directions. Essentially, the model learns only in ways that don’t interfere with what it already knows.

While effective, applying gradient projection at scale—especially for high-dimensional ViTs—is computationally costly. Calculating and managing these subspaces across layers becomes intractable. DualLoRA’s innovations elegantly resolve this efficiency barrier.

The Core Method: Inside DualLoRA

DualLoRA introduces a dual-adapter design that harmonizes stability and plasticity. Each layer in the ViT contains two parallel adapters: an Orthogonal Adapter for preserving old knowledge and a Residual Adapter for acquiring new knowledge. These are coordinated through a Dynamic Memory mechanism, enabling adaptive inference without replay.

A diagram illustrating the DualLoRA architecture with its Orthogonal and Residual adapters and the concept of gradient projection.

Figure 2. Overview of the DualLoRA framework. The orthogonal adapter preserves previous learning, while the residual adapter captures new task knowledge.

1. The Orthogonal Adapter (O): Guardian of Old Knowledge

The Orthogonal Adapter ensures stability by constraining updates to non-interfering directions. Where previous methods like InfLoRA performed projections in the gradient space—requiring expensive dual forward passes—DualLoRA operates efficiently in the feature space.

The key insight is that ViTs primarily rely on the class token—the first embedding—for classification. DualLoRA thus focuses on preserving this token’s behavior. By sampling a small set of data points from prior tasks, it constructs a feature basis \((\Phi_t)\) representing critical directions for those tasks.

When learning a new task \(t+1\), the update to the orthogonal adapter \(\Delta \mathbf{O}_{t+1}\) is projected to be orthogonal to these bases:

\[ \Delta \mathbf{O}_{t+1}^{i} \leftarrow \Delta \mathbf{O}_{t+1}^{i} - (\mathbf{\Phi}_{t}^{i})^{\top}\mathbf{\Phi}_{t}^{i}\Delta \mathbf{O}_{t+1}^{i}, \quad \forall i \in \{k, v\} \]

This projection prevents overwriting old class token features, thus mitigating forgetting. Since only a reduced subspace (\(m \ll d\)) is processed, the SVD operation needed to compute \(\Phi_t\) is much faster and memory-efficient than in previous approaches.

2. The Residual Adapter (R): Engine of New Learning

A purely orthogonal constraint can overly restrict the model, leaving little room for adaptation. To restore plasticity, DualLoRA introduces the Residual Adapter, designed to capture the novel components introduced by each new task.

This residual subspace (\(\Psi_t\)) represents newly learned directions absent from prior tasks:

\[ \Psi_t := \Phi_t^v - \Phi_{t-1}^v \]

The residual adapter’s updates are projected into this subspace:

\[ \Delta \mathbf{R}_{t+1} \leftarrow \boldsymbol{\Psi}_t^{\top}\boldsymbol{\Psi}_t \Delta \mathbf{R}_{t+1} \]

This strategy ensures the model gains new task-specific capacity while retaining previous knowledge integrity.

3. Dynamic Memory: Adapting on the Fly

During inference, the model must handle inputs without task labels. Simply applying all residual adapters simultaneously causes interference. Dynamic Memory (DM) solves this by weighting each residual adapter’s contribution according to task relevance.

When a test image is processed:

  1. The model computes an activation vector \(\mathbf{v}^{(l)}\).
  2. It measures cosine similarity between this vector and each stored residual basis \(\Psi_{\tau}\) across tasks:
\[ \omega_{\tau} = \frac{\|\Psi_{\tau} \cdot \mathbf{v}^{(l)}\|}{r_{\tau}\|\mathbf{v}^{(l)}\|} \]

These relevance scores dynamically scale the output of each residual adapter. Highly relevant task components receive higher weights, while irrelevant ones are suppressed. This makes DualLoRA context-aware and interference-free during inference.

4. Task Identification with Confidence

DualLoRA extends Dynamic Memory by introducing task identification and confidence calibration. For each test sample, the model compares its similarity vector \(\boldsymbol{\pi}^*\) to stored task prototypes \(\boldsymbol{\pi}_{\tau}\). The most similar task is predicted:

\[ \hat{k} = \arg\max_{\tau} g(\boldsymbol{\pi}_{\tau}, \boldsymbol{\pi}^{*}) \]

Then, a confidence margin \(\hat{\delta}\) is computed based on the score difference between the best and next-best matches. This confidence boosts the output for the predicted task:

\[ f_{\hat{k}}(\mathbf{h}^{(L)}) \leftarrow (1 + \hat{\delta}) \cdot f_{\hat{k}}(\mathbf{h}^{(L)}) \]

This simple yet effective calibration improves prediction reliability when task labels are unknown.

Experiments and Results

The researchers benchmarked DualLoRA and DualLoRA+ against leading PEFT-based continual learning methods—such as LoRA, L2P, DualPrompt, CodaPrompt, and InfLoRA—across ImageNet-R, CIFAR100, and Tiny-ImageNet datasets. Performance was measured using:

  • Average Accuracy (ACC) — higher is better.
  • Forgetting (FT) — lower is better.

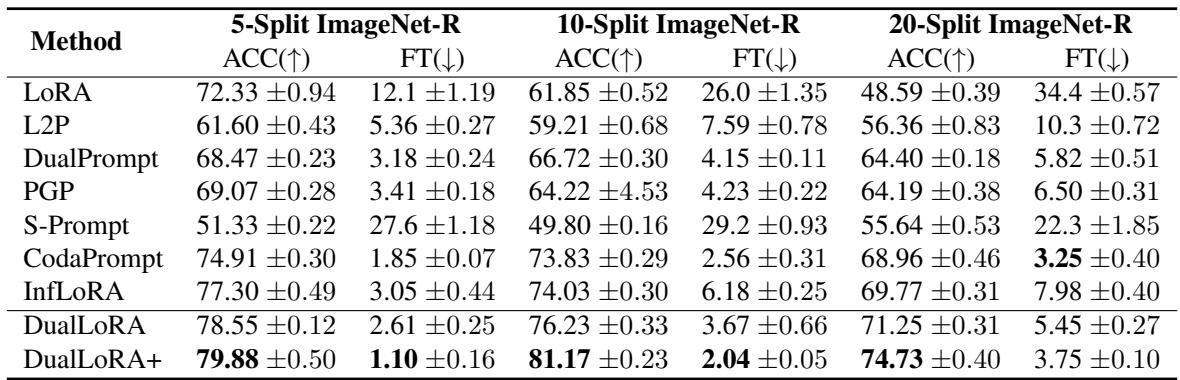
Table showing DualLoRA’s superior performance on the ImageNet-R benchmark across 5, 10, and 20 task splits.

Table 1. DualLoRA achieves top results on ImageNet-R across all task splits, with the DualLoRA+ variant setting new benchmarks.

Table showing DualLoRA’s strong results on CIFAR100 and Tiny-ImageNet benchmarks.

Table 2. Consistent gains on CIFAR100 and Tiny-ImageNet validate DualLoRA’s robustness across datasets.

Across all benchmarks, DualLoRA ranks among the very best. It matches or surpasses InfLoRA’s accuracy while being significantly more efficient. The DualLoRA+ variant, incorporating enhanced task identity prediction, further pushes performance boundaries.

Line plots showing that DualLoRA+ maintains higher average accuracy as the number of tasks increases on ImageNet-R and CIFAR100.

Figure 3. DualLoRA+ maintains high accuracy as tasks accumulate, demonstrating effective resistance to forgetting.

Why It Works: Ablation Insights

To test the contribution of each component, the authors conducted an ablation study where parts of DualLoRA were incrementally added or removed.

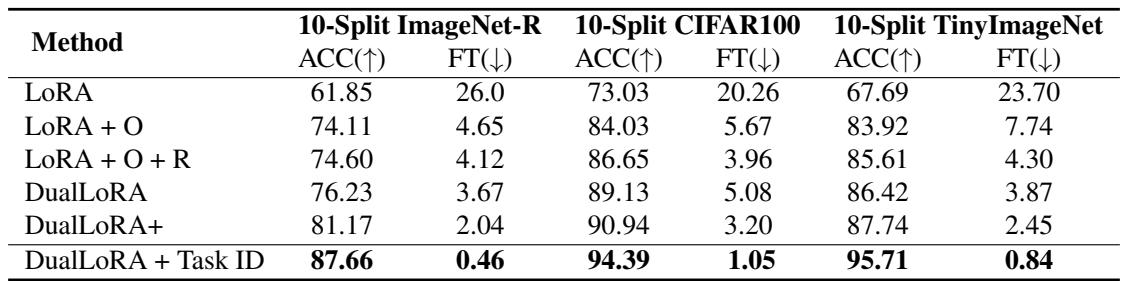
Table from the ablation study, showing how performance improves as each component (Orthogonal adapter, Residual adapter, Task ID prediction) is added.

Table 3. Each module (O for Orthogonal Adapter, R for Residual Adapter, Task ID prediction) adds measurable improvements, validating the design.

The findings:

  1. Vanilla LoRA suffers heavy forgetting.
  2. Adding the Orthogonal Adapter dramatically boosts stability.
  3. Adding the Residual Adapter enhances plasticity, improving accuracy.
  4. Including Task Identification yields the full DualLoRA benefit, maximizing both performance and efficiency.

Every layer of the design contributes meaningfully to the final outcome.

Efficiency: Faster Training and Inference

Many prompt-based methods double inference or training time due to dual forward passes. InfLoRA limits inference lag but remains computationally intensive during training. DualLoRA strikes balance—it minimizes FLOPs while keeping inference fast.

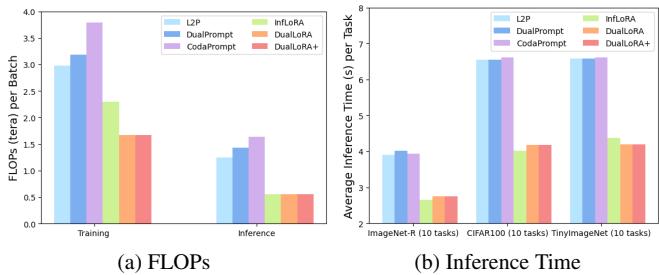
Bar charts comparing the computational FLOPs and inference time of DualLoRA against other methods.

Figure 4. DualLoRA achieves the lowest training FLOPs and competitive inference speed, outperforming slower prompt-based approaches.

It achieves this efficiency by extracting smaller subspaces around the class token and eliminating redundant double passes, making it both lightweight and scalable for large ViTs.

Conclusion and Takeaways

DualLoRA represents a major advancement in replay-free continual learning for foundation models. Through its elegant dual-adapter design and dynamic memory system, it successfully balances stability and plasticity—a long-standing challenge in AI.

Key takeaways:

  1. Dual-Adapter Architecture: Combining orthogonal (stability) and residual (plasticity) adapters allows efficient, balanced continual learning.
  2. Computational Efficiency: By focusing on the class-token subspace, DualLoRA avoids costly full-model projections, accelerating both training and inference.
  3. Dynamic Memory & Task Awareness: The system intelligently reuses relevant task subspaces during inference, enabling accurate predictions without task labels.

DualLoRA sets a new standard for efficient, scalable continual learning on large vision models—an encouraging step toward machine learning systems that, like humans, can learn continuously without forgetting the past.