Imagine a self-driving car learning to navigate your city. It first masters the highways, then the downtown grid, and finally the winding suburban roads. Now imagine that learning to recognize a new type of pedestrian crossing makes it forget what a stop sign looks like. Such a failure would be disastrous.

This phenomenon—known as catastrophic forgetting—is one of the major obstacles in building robust artificial intelligence systems. It raises a fundamental question: How can a model learn continuously from new data without erasing the knowledge it already possesses? This challenge lies at the core of Continual Learning (CL).

The difficulty intensifies under a realistic setting called task-free online continual learning. “Online” means the model sees every data point only once, just like humans do. “Task-free” means there are no predefined boundaries or labels indicating when tasks begin or end—the data keeps streaming, with distribution shifts occurring unpredictably.

A recent paper, “Online-LoRA: Task-free Online Continual Learning via Low Rank Adaptation”, proposes a remarkably effective solution to this problem. The authors introduce Online-LoRA, a framework that combines the power of pre-trained Vision Transformers (ViTs) with a lightweight adaptation method called Low-Rank Adaptation (LoRA). Together, they enable the model to learn continuously and efficiently while outperforming previous state-of-the-art approaches.

In this post, we unpack the key insights behind Online-LoRA, explore how it works, review its impressive experimental results, and discuss its implications for the future of lifelong learning in AI.

Setting the Stage: The Landscape of Continual Learning

Before diving into Online-LoRA, it helps to understand the broader landscape of continual learning.

The Continual Learning Dilemma

Continual Learning aims to train a model across a sequence of data distributions that evolve over time. CL approaches are generally categorized using two dimensions:

  1. Task-based vs. Task-free:
  • Task-based methods know when one task ends and another begins (e.g., “first learn cats, now dogs”).
  • Task-free methods receive no such information—the data flows continuously, often blending old and new distributions.
  1. Offline vs. Online:
  • Offline methods can train for multiple epochs on the same task data.
  • Online methods get a single pass over the data stream, requiring immediate updates.

The most challenging and realistic configuration is the online, task-free setting—essential for dynamic environments such as robotics, autonomous vehicles, and adaptive healthcare systems. The absence of explicit boundaries and limited data access make traditional training schemes ineffective here.

The Rise of Pre-trained Models and LoRA

Large pre-trained models like Vision Transformers (ViTs) have revolutionized computer vision by learning general, transferable representations from massive datasets. Instead of training from scratch, practitioners now fine-tune these models to new tasks—a process that is more efficient and performant.

However, fully fine-tuning a massive model (e.g., 86M+ parameters) is costly and can still cause catastrophic forgetting. To counter this, Parameter-Efficient Fine-Tuning (PEFT) methods were introduced.

One powerful PEFT technique is Low-Rank Adaptation (LoRA), which allows models to update only a small subset of parameters. LoRA freezes the original weights \( W_{init} \) and learns a compact offset \( \Delta W \) decomposed into two low-rank matrices \( B \) and \( A \):

\[ \Delta W = BA \]

Here, \( B \in \mathbb{R}^{d \times r} \) and \( A \in \mathbb{R}^{r \times k} \), with the rank \( r \ll \min(d, k) \). Only \( A \) and \( B \) are trained, significantly reducing the computational load while retaining expressive power.

LoRA has been successfully applied to offline task-based continual learning, but applying it to task-free online settings—where the system must self-identify distribution changes—remains an open challenge. That’s precisely where Online-LoRA comes in.

The Core Method: How Online-LoRA Works

Online-LoRA introduces two innovations that make LoRA viable for online, task-free continual learning:

  1. Loss-Guided Model Adaptation – automatically detects when the data distribution changes.
  2. Online Weight Regularization – protects previously learned knowledge efficiently using minimal memory.

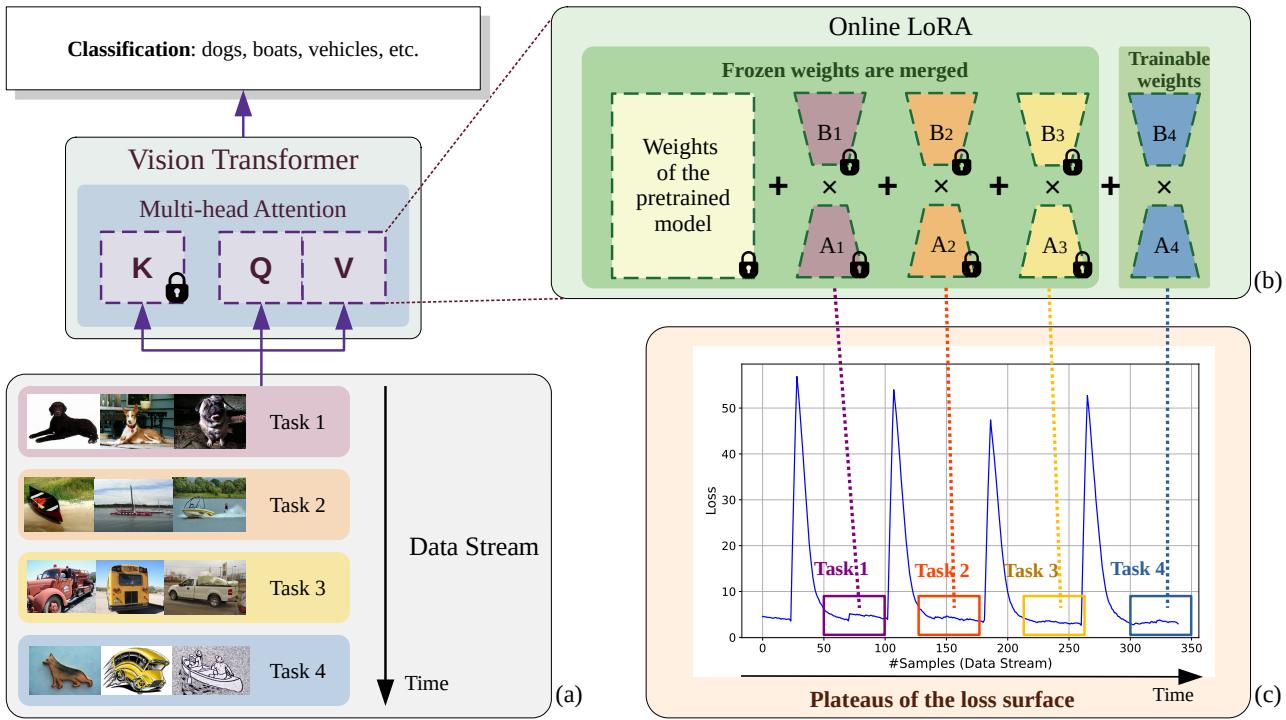
Figure 1 provides a high-level overview of the Online-LoRA framework. (a) A continuous data stream flows over time. (b) The model dynamically adds new LoRA parameters (A4, B4) while freezing and merging old ones. (c) This process is triggered by detecting plateaus in the loss surface, which signal that the model has converged on the current data distribution.

Figure 1. Overview of Online-LoRA. As data streams in, every plateau in the loss surface prompts the creation of a new LoRA module, while previous modules are frozen and merged into the ViT weights.

1. Loss-Guided Model Adaptation: Learning Without Boundaries

When should a model switch to learning new information versus consolidating old knowledge? Online-LoRA’s answer lies in the model’s loss surface—a curve indicating how well it’s learning.

  • Declining loss: the model is learning effectively from current data.
  • Sudden loss spike: data distribution has likely shifted.
  • Flat, low loss (plateau): the model has converged, meaning it’s time to consolidate.

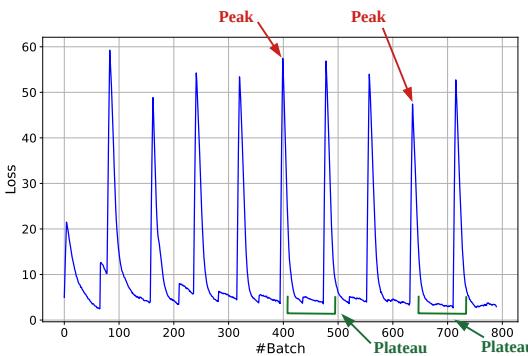
Figure 4 shows a visualization of the loss surface over time. Sharp peaks indicate shifts in the data distribution, while the flat, low-loss regions are the plateaus that Online-LoRA uses as signals to adapt.

Figure 4. Visualization of Online-LoRA’s loss surface on CIFAR-100. Peaks signal data shifts, and stable plateaus mark moments for adaptation.

To act on this, Online-LoRA continuously monitors the training loss using a sliding window. When the mean and variance of the loss within the window fall below predefined thresholds, the system detects a plateau. At that moment:

  1. The currently trainable LoRA matrices \( (A_t, B_t) \) are frozen.
  2. They are merged into the main ViT weights, embedding learned knowledge permanently.
  3. A fresh, randomly initialized pair \( (A_{t+1}, B_{t+1}) \) is created to learn from new data.

By tying adaptation to intrinsic training dynamics instead of preset boundaries, Online-LoRA makes continual learning self-regulating and responsive.

2. Online Parameter Importance Estimation: Efficiently Preventing Forgetting

Even with adaptive modules, new learning can still interfere with old knowledge. To mitigate this, Online-LoRA employs a lightweight online regularization that identifies and protects important parameters.

Traditional methods like Elastic Weight Consolidation (EWC) compute importance across all parameters via the Fisher Information Matrix—a prohibitively large computation for ViTs (tens of millions of parameters).

Online-LoRA introduces two efficiency breakthroughs:

a) Focus Regularization on LoRA Parameters Only. Instead of computing importance for all weights, Online-LoRA tracks only the small, trainable LoRA matrices. For a ViT-B/16 with LoRA rank 4, this reduces the count from ~86M parameters to only ~150K (≈0.17%), enabling real-time updates.

b) Use a Minimal Hard Buffer. To estimate the importance of parameters, the model needs examples to measure sensitivity. Instead of storing large replay buffers, Online-LoRA maintains a hard buffer with just four high-loss samples—those the model finds most challenging. This compact set provides strong signals on which knowledge needs preservation, while remaining privacy- and memory-efficient.

Combining these ideas, the importance of each LoRA parameter is computed as:

\[ \Omega_{ij}^{A,l} = \frac{1}{N} \sum_{k=1}^{N} \nabla_{W_{ij}^{A,l}} \log p(x_k|\theta) \circ \nabla_{W_{ij}^{A,l}} \log p(x_k|\theta) \]\[ \Omega_{ij}^{B,l} = \frac{1}{N} \sum_{k=1}^{N} \nabla_{W_{ij}^{B,l}} \log p(x_k|\theta) \circ \nabla_{W_{ij}^{B,l}} \log p(x_k|\theta) \]

Using these weights, the overall learning objective becomes:

\[ \min_{W^A, W^B} \mathcal{L}(F(X;\theta), Y) + \mathcal{L}(F(X_B;\theta), Y_B) + L_{\text{LoRA}}(W^A, W^B) \]

where the three components represent:

  1. The loss on the current batch,
  2. The loss on hard buffer samples, and
  3. The LoRA regularization penalty protects critical parameters from drastic updates.

This efficient Bayesian-inspired regularization makes Online-LoRA capable of learning continuously while preserving previous knowledge.

Experiments and Results: Putting Online-LoRA to the Test

The authors ran extensive experiments across several benchmark scenarios, each testing different facets of continual learning.

Experimental Settings

Online-LoRA was evaluated under three key scenarios:

  1. Disjoint Class-Incremental: Tasks have distinct, non-overlapping class sets.
  2. Si-Blurry Class-Incremental: Tasks overlap and boundaries blur dynamically.
  3. Domain-Incremental: The same classes appear, but input style or domain changes (e.g., photos → sketches).

Baselines include rehearsal-based methods (ER, DER++, PCR), regularization methods (EWC++), and prompt-based methods (L2P, MVP).

Disjoint Class-Incremental Results

In this setting, Online-LoRA maintains the highest final accuracy and lowest forgetting across multiple datasets (CIFAR-100, ImageNet-R, ImageNet-S, and CUB-200) with both ViT-B/16 and ViT-S/16 architectures.

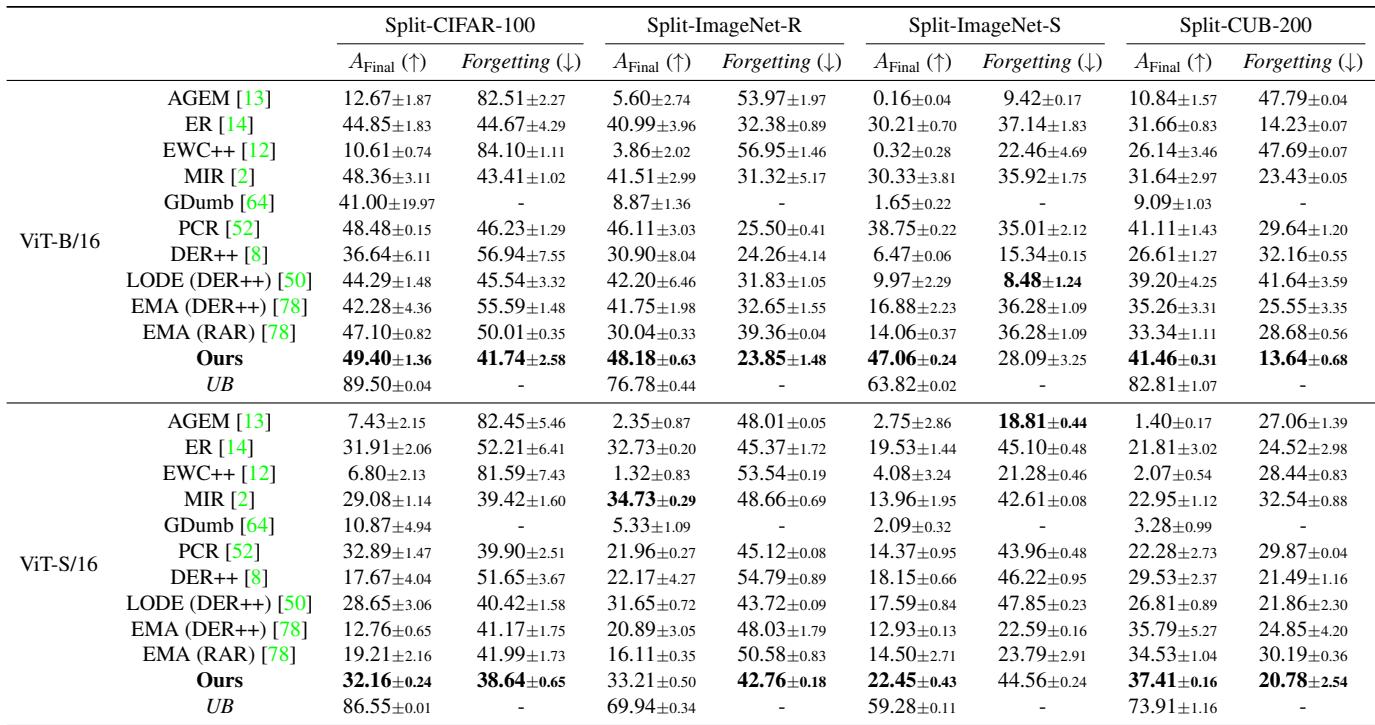
Table 1 shows the results for disjoint class-incremental learning. Online-LoRA (Ours) achieves the highest final accuracy and lowest forgetting on multiple benchmarks, often by a significant margin.

Figure/Table 1. Disjoint class-incremental results. Online-LoRA outperforms every existing method across datasets and architectures.

Si-Blurry Class-Incremental Results

In the more dynamic Si-Blurry environment, Online-LoRA continues to excel. It not only surpasses prompt-based methods (L2P, MVP) by wide margins but maintains strong anytime inference accuracy throughout the data stream.

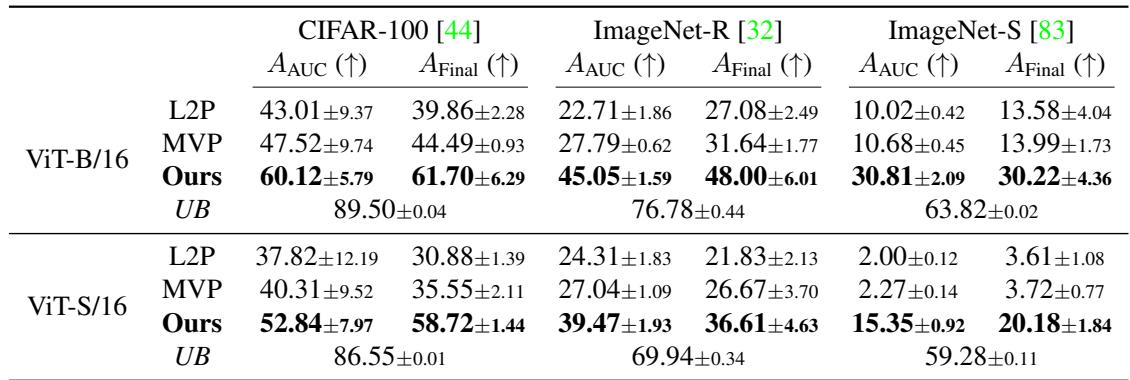
Table 2 presents the results for the challenging Si-Blurry scenario. Online-LoRA achieves a massive improvement in both final accuracy (A_Final) and anytime inference accuracy (A_AUC) compared to other prompt-based methods.

Figure/Table 2. Si-Blurry learning results. Online-LoRA achieves higher accuracy and strong stability during streaming learning.

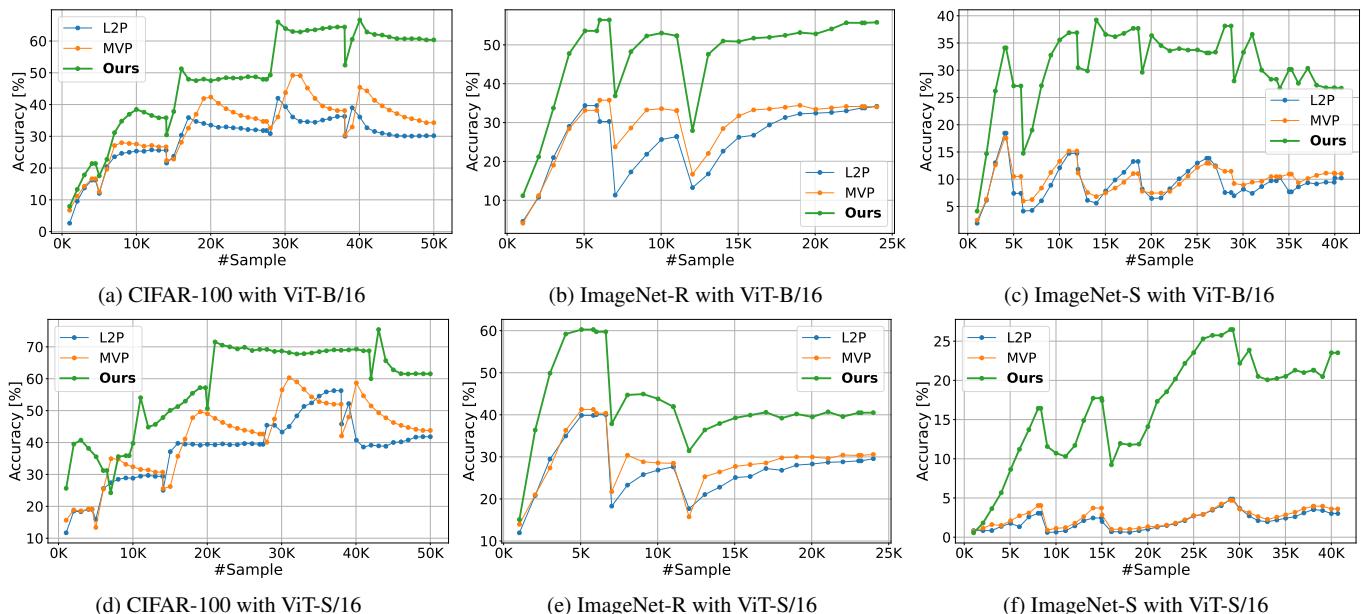
Figure 2 plots the average accuracy as the model sees more samples. Online-LoRA (green line) consistently maintains a higher accuracy curve, demonstrating its superior ability to learn on the fly.

Figure 2. Online-LoRA maintains top-level performance throughout training, not just at the end—key for real-world continuous inference tasks.

Domain-Incremental Results

Online-LoRA shines even brighter when adapting across domains. On the CORe50 dataset, it achieves a final accuracy of 93.7%, closing almost the entire gap with the upper-bound (95.6%)—while entirely avoiding catastrophic forgetting.

Table 3 shows the domain-incremental learning results. Online-LoRA achieves near-perfect performance with zero forgetting, closing a large portion of the gap to the theoretical upper bound.

Figure/Table 3. Domain-incremental performance comparison on CORe50. Online-LoRA nearly matches supervised upper-bound performance with zero forgetting.

Scaling with Longer Task Sequences

A robust continual learner should withstand increasing numbers of tasks. As shown below, while other methods degrade sharply with more tasks, Online-LoRA remains remarkably resilient due to its loss-based adaptation and continual regularization.

Figure 3 tracks the accuracy on specific old tasks as new tasks are learned. The pink line representing Online-LoRA stays significantly higher than the others, demonstrating its powerful ability to mitigate catastrophic forgetting over long sequences.

Figure 3. Validation accuracy across multiple task sequences. Online-LoRA retains high performance and minimal forgetting over time.

Ablation Studies: Why It Works

To confirm the value of each component, the authors conducted ablation experiments that removed the “Incremental LoRA” mechanism and/or the “Hard loss” regularization.

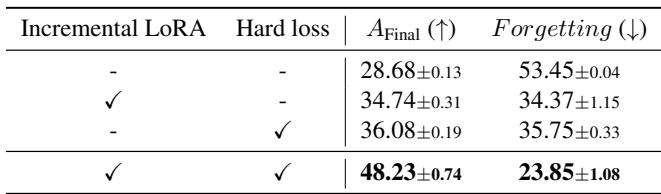
Table 6 shows the ablation study results. Removing either the “Incremental LoRA” mechanism or the “Hard loss” regularization causes a significant drop in accuracy and an increase in forgetting. The full model with both components performs best.

Figure/Table 6. Ablation study results highlighting the impact of each component.

Removing either element drastically reduces performance. Only when both are used together does Online-LoRA reach its best results—proving the synergy between dynamic LoRA updates and online regularization.

Conclusion and Outlook

Online-LoRA represents a major advancement in continual learning. By turning the model’s own loss into a signal for adaptation and regularizing efficiently using low-rank structures, it elegantly achieves task-free online learning without rehearsal buffers or task boundaries.

Key takeaways:

  • Self-Regulating Expansion: Loss plateaus naturally signal when to consolidate learning and start adapting to new data.
  • Extreme Efficiency: Focusing on LoRA parameters enables online regularization of massive ViTs using only minimal memory and computation.
  • Broad Robustness: Consistent state-of-the-art results across classes, domains, and varying task sequences show unmatched stability and flexibility.

As AI systems increasingly operate in continuously evolving environments, methods like Online-LoRA will be crucial. The paper not only demonstrates technical ingenuity but also charts a practical path toward lifelong learning—where intelligent agents adapt seamlessly and remember indefinitely.