Unlocking System 2 Thinking in AI Agents: Monte Carlo Tree Diffusion

Imagine you are playing a complex game of chess. Sometimes, you make a move instantly based on intuition—a quick pattern match. Other times, you sit back and simulate several moves into the future, weighing options, discarding bad paths, and refining your strategy before touching a piece.

In cognitive science, these are often referred to as System 1 (fast, instinctive) and System 2 (slow, deliberative) thinking.

In the world of AI planning, Diffusion Models—the same tech behind DALL-E and Midjourney—have recently become excellent “System 1” planners. They can generate complex trajectories in one go. However, they struggle with “System 2” reasoning. If you give a standard diffusion model more time to think, it doesn’t necessarily get smarter; it just generates another random guess.

This blog post explores a new framework called Monte Carlo Tree Diffusion (MCTD). This method bridges the gap between the generative power of diffusion models and the strategic depth of Monte Carlo Tree Search (MCTS). By reading this, you will understand how we can finally allow diffusion planners to “think” longer to produce better plans, solving complex long-horizon tasks that stump standard models.

The Problem: When Intuition Isn’t Enough

Diffusion models have revolutionized planning by treating trajectory generation as a denoising problem. Instead of predicting one action at a time (which leads to error accumulation), a diffusion planner generates the entire path at once.

The trajectory is often represented as a matrix \(\mathbf{x}\) containing states \(s\) and actions \(a\):

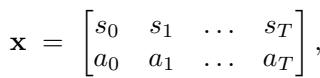
A model \(p_{\theta}(\mathbf{x})\) learns to denoise this matrix from random Gaussian noise into a feasible plan. To make the agent actually solve a task (like reaching a goal), the sampling is guided by a function \(J_{\phi}(\mathbf{x})\) that estimates the value or return of a trajectory:

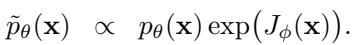
While effective, this approach has a ceiling. Standard diffusion planners like Diffuser offer limited “inference-time scalability.” If the model fails to find a path through a giant maze, running it for twice as many steps usually yields diminishing returns. It lacks a structured way to explore the solution space, prune bad ideas, and refine good ones. It lacks the ability to reason.

The Solution: Monte Carlo Tree Diffusion (MCTD)

To solve this, researchers have looked to Monte Carlo Tree Search (MCTS). MCTS is the algorithm behind AlphaGo’s success. It builds a search tree by simulating future outcomes, allowing the agent to focus computational resources on promising paths.

MCTD combines these two worlds. It reconceptualizes the diffusion denoising process as a tree-structured search.

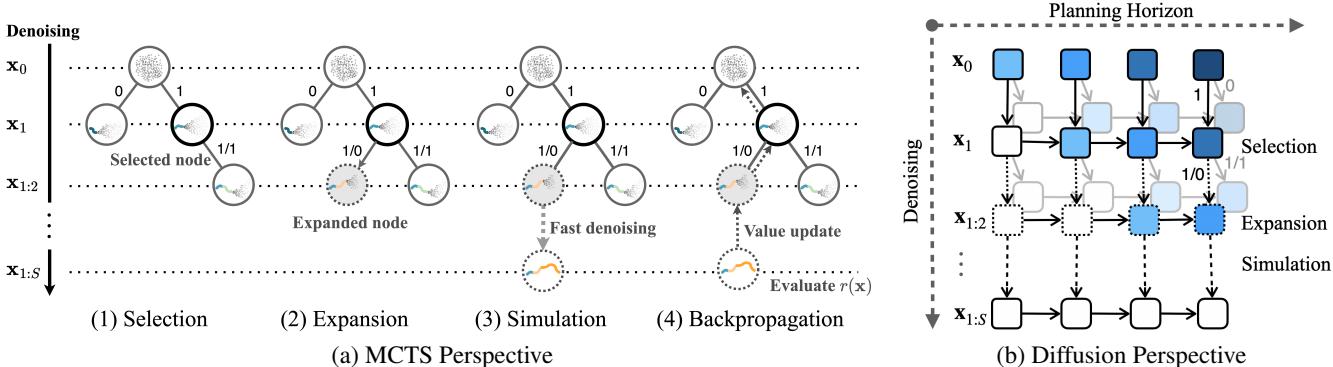
As shown in Figure 1 above, MCTD operates on two axes:

1. Planning Horizon (Horizontal): Moving forward in time within the task.
2. Denoising Depth (Vertical): Refining the quality of the plan from noise to clarity.

By marrying these concepts, MCTD achieves three critical innovations that allow it to scale intelligence with compute.

Innovation 1: Denoising as Tree-Rollout

Traditional MCTS builds a tree state-by-state. If a plan requires 500 steps, the tree becomes impossibly deep (\(Depth=500\)).

MCTD solves this by breaking the trajectory \(\mathbf{x}\) into a sequence of sub-plans (e.g., segments of 50 steps). The nodes in the search tree are not single states, but these sub-plans. This makes the tree much shallower and manageable.

The planner uses a “semi-autoregressive” approach. It generates the first sub-plan, locks it in, and then conditions the next sub-plan on the first. Mathematically, this approximates the full trajectory probability as a product of sub-plans:

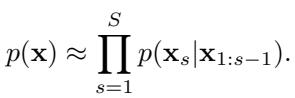
This allows the agent to construct a plan piece-by-piece, but with each piece being a coherent chunk generated by the diffusion model.

Innovation 2: Guidance Levels as “Meta-Actions”

In a standard search tree (like for Chess), the branches (edges) represent discrete moves (e.g., “Pawn to E4”). But in robotics, the action space is continuous and infinite. You can’t branch on every possible motor torque.

MCTD introduces a brilliant abstraction: Meta-Actions.

Instead of branching on physical actions, the tree branches on Guidance Levels. At each step of the tree, the agent decides how to use the diffusion model:

• NO_GUIDE (Exploration): Sample from the prior. This asks the model, “What is a physically plausible trajectory here?” without forcing it toward the goal. This encourages diversity.
• GUIDE (Exploitation): Sample using the reward function. This asks, “Find me a path that gets high reward.”

By dynamically switching between these modes, the search tree balances exploring new possibilities and refining promising ones. The conditional probability now includes this guidance schedule \(\mathbf{g}\):

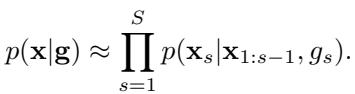
Innovation 3: Jumpy Denoising as Fast Simulation

In MCTS, every time you add a new node, you need to “simulate” to the end to see if it’s a good position. For diffusion, generating a full plan is slow and expensive.

MCTD uses Jumpy Denoising (based on DDIM) for the simulation step. Once a node (sub-plan) is created, the system needs to guess how the rest of the trajectory looks. Instead of a high-quality slow generation, it runs a “fast forward” version, skipping many denoising steps:

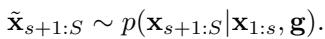
This provides a quick, rough estimate of the plan’s final quality (\(\tilde{\mathbf{x}}\)), which is enough to guide the search without burning the entire computational budget.

The MCTD Algorithm in Action

MCTD follows the classic four-step MCTS loop, adapted for generative modeling.

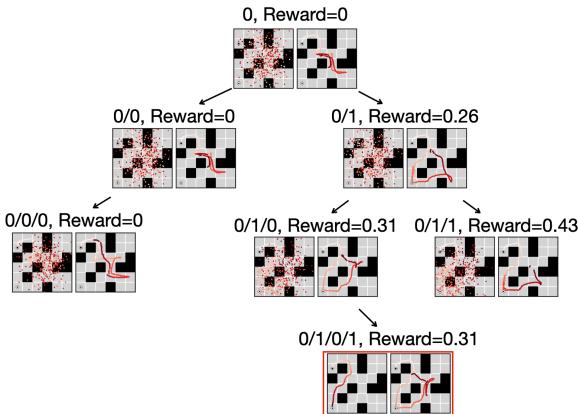
1. Selection: The algorithm traverses the current tree. It uses the Upper Confidence Bound (UCB) to pick the most promising node that hasn’t been fully explored. It balances nodes with high value (exploitation) and nodes that haven’t been visited much (exploration).
2. Expansion: Once a leaf node is reached, the algorithm expands the tree. It generates a new sub-plan using the diffusion model. It chooses a “meta-action” (Guidance or No Guidance) to determine how this new segment is generated.
3. Simulation: To evaluate this new partial plan, the rest of the trajectory is completed using Jumpy Denoising. This is a fast, approximate rollout to the end of the episode.
4. Backpropagation: The quality of the simulated full plan is evaluated (e.g., “Did we reach the goal?”). This value is propagated back up the tree, updating the statistics of all parent nodes.

The algorithm effectively “thinks” by growing this tree. As it runs more iterations, it finds better branches and abandons dead ends.

Experimental Results

Does adding this “System 2” structure actually help? The researchers tested MCTD on challenging benchmarks like OGBench, which includes long-horizon maze navigation and robotic manipulation.

1. Long-Horizon Mazes

The most direct test of planning is a complex maze. Standard diffusion models often get stuck in local optima or “hallucinate” paths through walls when the horizon is long.

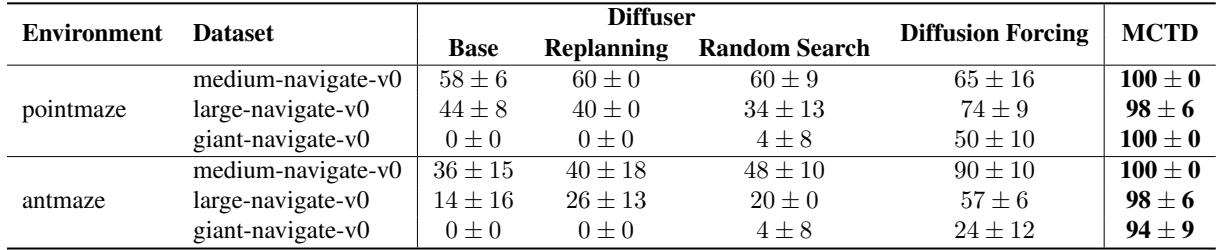
As shown in Table 1, MCTD achieves near-perfect success rates (94-100%) on “Giant” mazes where standard Diffuser and even “Diffusion Forcing” (a strong baseline) fail significantly.

A visual comparison clarifies why:

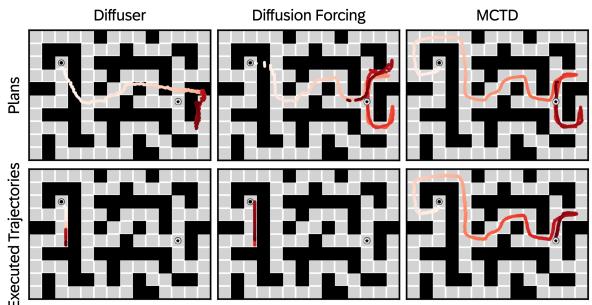
In Figure 2, you can see that baselines (Diffuser) produce disconnected or invalid paths. MCTD, by systematically searching and pruning, finds a coherent path to the goal.

2. Robotic Manipulation

The researchers also tested MCTD on a robot arm task manipulating multiple cubes. This is difficult because it requires distinct stages: move cube A, then move cube B.

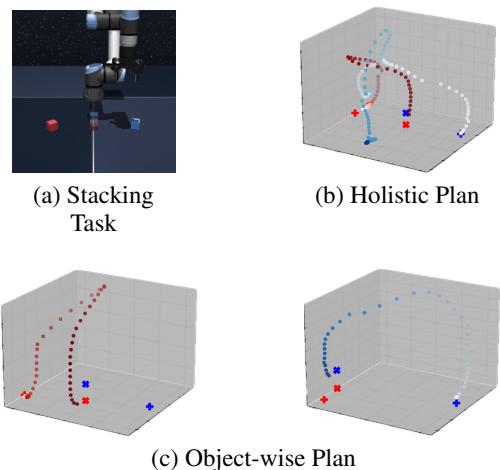
MCTD (specifically a variant called MCTD-Replanning) showed a strong ability to handle multi-object sequencing. The tree search allows it to separate the sub-goals (moving different cubes) rather than trying to mash all movements into one entangled plan.

3. Visual Planning (Partial Observability)

Can this work when the robot only sees pixels? The team created a “Visual Pointmaze” where the input is images, not coordinates. This creates partial observability—the robot doesn’t know exactly where it is, only what it sees.

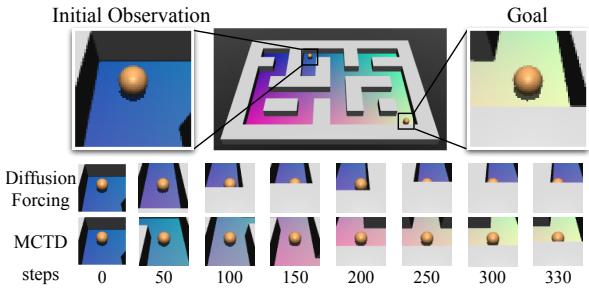
The results (Table 3 below) show that MCTD significantly outperforms baselines in this harder setting. The tree search helps manage the uncertainty inherent in visual observations.

4. The Power of “Thinking Longer”

The central claim of MCTD is Inference-Time Scalability. If we give the model more time to think (more denoising steps/budget), does it perform better?

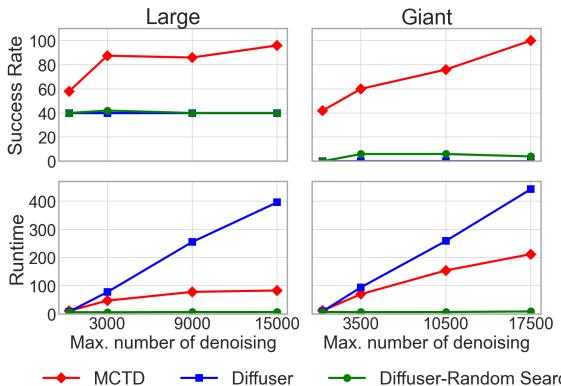
Figure 6 is perhaps the most important result.

• Diffuser (Orange/Green): The success rate stays flat even as you increase the compute budget. It hits a performance ceiling.
• MCTD (Blue): The success rate climbs steadily as the budget increases, reaching nearly 100% on the Giant maze.

This proves that MCTD effectively converts computation into intelligence, a hallmark of System 2 reasoning.

Ablation Studies: What Matters?

The researchers performed several ablation studies to understand which components drive success.

• Greedy Search vs. Tree Search: A simple greedy search (picking the best of \(K\) options at each step) failed on Giant maps (0% success). The ability to backtrack and maintain a full tree is essential (Table 4).

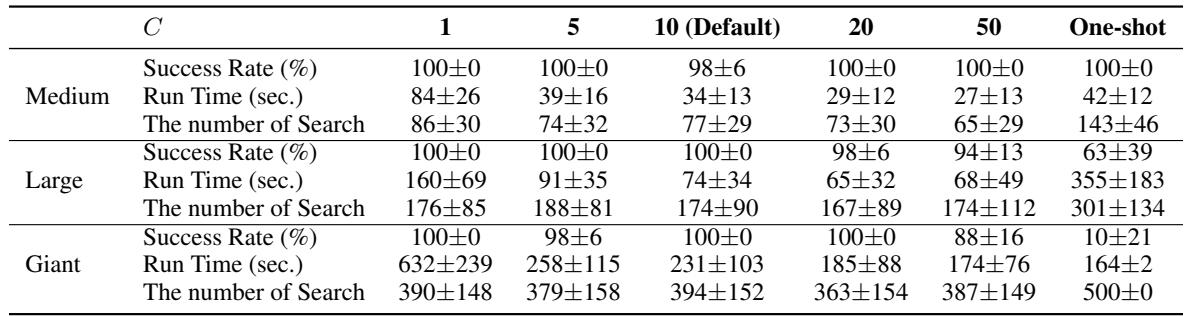
• Jumpy Denoising Scale: How “jumpy” should the simulation be? If it’s too fast (One-shot), accuracy drops (10% success on Giant). If it’s too slow (\(C=1\)), runtime explodes. A balanced scale (\(C=10\)) offers the best trade-off.

Conclusion

Monte Carlo Tree Diffusion represents a significant step forward in AI planning. By integrating the structured, deliberative search of MCTS with the generative capabilities of diffusion models, it solves the “inference-time scalability” problem.

MCTD allows agents to:

1. Reason over long horizons by breaking plans into manageable sub-trees.
2. Balance exploration and exploitation using guidance levels as meta-actions.
3. Think efficiently using jumpy denoising for fast simulations.

This framework moves us closer to general-purpose agents that don’t just react to their environment, but genuinely plan, reason, and adapt to solve complex problems. Future work involves making the search even faster and learning the meta-actions automatically, paving the way for even more capable System 2 agents.