Distilling Giants: How DISTILLM-2 Uses Contrastive Learning to Build Better Small LLMs

The race for larger, more capable Large Language Models (LLMs) has dominated headlines, but a parallel revolution is happening in the world of efficiency. Deploying massive models like GPT-4 or Llama-3-70B is computationally expensive and slow. This has driven the need for Knowledge Distillation (KD)—the process of compressing the intelligence of a massive “teacher” model into a smaller, faster “student” model.

While KD is effective, standard methods often treat all training data effectively the same, regardless of whether it came from the genius teacher or the learning student. This lack of nuance leads to suboptimal compression.

In this post, we dive into DISTILLM-2, a new research paper that introduces a “contrastive” approach to distillation. By mathematically aligning the loss function with the specific type of data being processed (teacher vs. student outputs), the researchers have achieved state-of-the-art results across instruction following, coding, and math tasks.

The Problem with Symmetric Distillation

To understand why DISTILLM-2 is necessary, we first need to look at how LLM distillation typically works. The goal is to minimize the divergence between the teacher’s probability distribution (\(p\)) and the student’s distribution (\(q_\theta\)).

The most common tool for this is the Kullback-Leibler (KL) divergence, typically calculated at the token level:

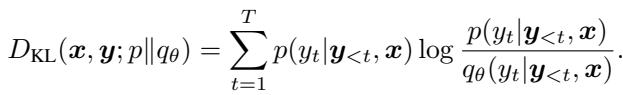
Here, the loss measures how much the student deviates from the teacher. Standard approaches often use Forward KL (matching the teacher’s high-probability regions) or Reverse KL (forcing the student to avoid low-probability regions).

However, current methods have a blind spot: they often apply identical loss functions to both Teacher-Generated Outputs (TGOs) and Student-Generated Outputs (SGOs).

• TGOs are high-quality “ground truth” sequences.
• SGOs are exploratory sequences generated by the student, which may contain errors or hallucinations.

Treating these two distinct data sources symmetrically ignores their inherent differences. The authors of DISTILLM-2 argue that to maximize performance, we need a synergy between the loss formulation and the data type.

Background: The Skewed Approach

DISTILLM-2 builds upon a previous method called DistiLLM, which introduced the concept of Skew KL (SKL) and Skew Reverse KL (SRKL).

Standard KL divergence has issues with “mode-averaging” (producing generic, safe responses) or “mode-collapse” (getting stuck on one specific response). To fix this, Skew KL mixes the teacher and student distributions using a mixing coefficient \(\alpha\).

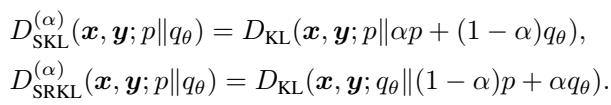
By interpolating between distributions (e.g., \(\alpha p + (1-\alpha)q_\theta\)), the training becomes smoother and avoids the extremes of standard KL. DISTILLM-2 adopts these skewed objectives as its mathematical backbone but fundamentally changes how and when they are applied.

The Core Method: Contrastive Distillation

The heart of DISTILLM-2 is a Contrastive Approach for LLM Distillation (CALD). The intuition is similar to Direct Preference Optimization (DPO) used in Reinforcement Learning: we want to increase the likelihood of “good” responses and decrease the likelihood of “bad” ones.

In the context of distillation:

1. Teacher Responses (\(y_t\)): Represent desirable behavior. We want to “pull up” the student’s probability for these.
2. Student Responses (\(y_s\)): Often contain deviations or errors. We want to “push down” the student’s probability for these (specifically, where the student is confident but the teacher is not).

Why Not Just Use DPO?

You might ask, why not just apply DPO directly by treating the teacher as the “winner” and the student as the “loser”? The researchers found that blindly applying DPO to distillation (a method they call DPKD) leads to reward hacking.

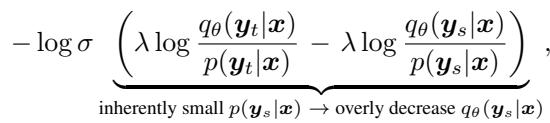
As shown above, because the teacher’s probability for a student’s mistake (\(p(y_s|x)\)) is inherently small, the loss function creates a massive gradient that excessively penalizes the student. This destroys the student’s linguistic capabilities rather than refining them.

The CALD Solution

DISTILLM-2 solves this by assigning specific loss functions to specific data types. It uses SKL for teacher outputs (to learn the “correct” distribution) and SRKL for student outputs (to correct the “incorrect” distribution).

The resulting loss function is a balanced sum of these two objectives:

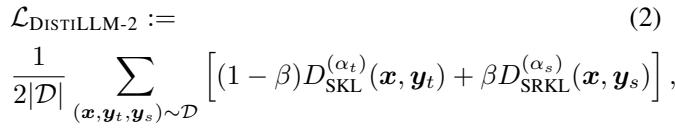
Here, \(\beta\) controls the balance between learning from the teacher (SKL) and self-correction (SRKL).

Visualizing the Dynamics

To understand why this split is vital, look at the behavior of KL and Reverse KL (RKL) in the figure below.

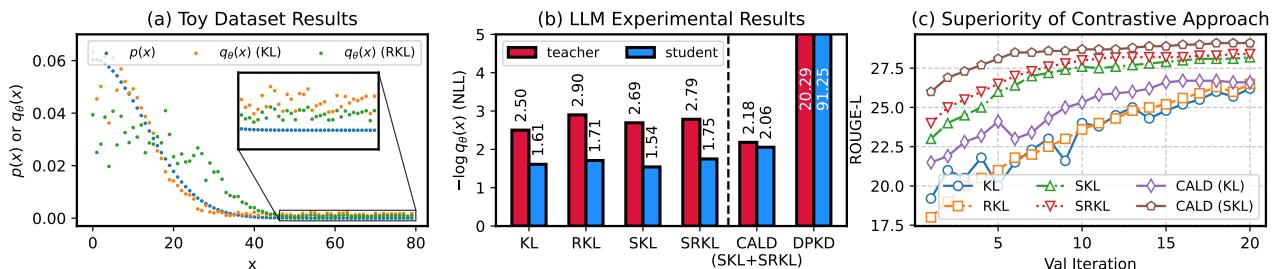
• Panel (a): Notice the “Pulling-up” effect of KL (orange) at the peak of the distribution—it encourages the student to match the teacher’s high confidence. Conversely, RKL (green) has a “Pushing-down” effect at the tails—it penalizes the student for assigning probability to things the teacher thinks are unlikely.
• Panel (b): This bar chart shows the Negative Log-Likelihood (NLL). The proposed CALD method (green/orange split) achieves a healthy balance. Compare this to DPKD (far right), where the student NLL explodes to 91.25, indicating the model has been broken by the objective function.
• Panel (c): The combination of SKL and SRKL (CALD-SKL) converges faster and reaches a higher ROUGE-L score than using standard KL or SKL alone.

Optimizing the Data and The Curriculum

Having a new loss function is great, but DISTILLM-2 goes further by optimizing what data goes into that function and how the training evolves over time.

1. Data Curation: Who generates what?

The researchers asked a crucial question: Should we replace teacher outputs with even better responses (e.g., from GPT-4) or use “speculative decoding” to mix distributions?

Surprisingly, the answer is no.

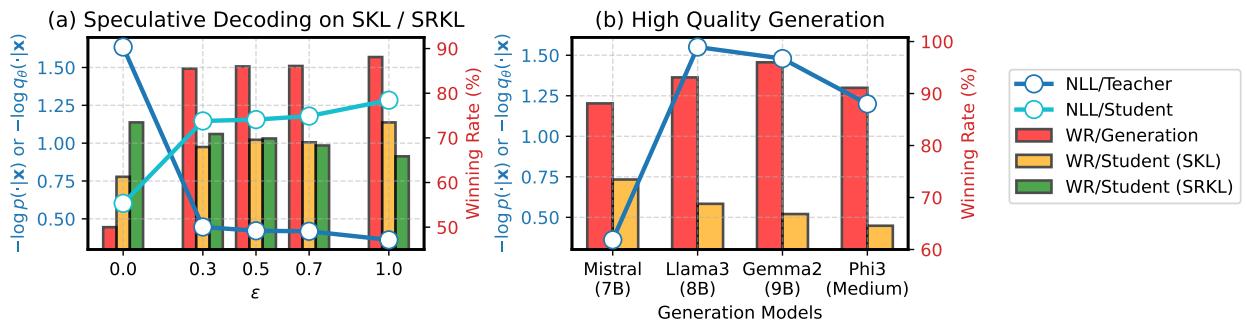
• Figure 2(a): Using speculative decoding (mixing student and teacher tokens) actually hurts performance compared to using pure teacher outputs for the SKL term (orange bars).
• Figure 2(b): Even replacing the teacher’s output with a stronger model (e.g., using Llama-3 to teach a Mistral student) doesn’t guarantee better distillation.

The takeaway: The effectiveness of the SKL term relies on the high probability assigned by the teacher model itself. The goal is to match the teacher’s distribution, not necessarily to generate the “best” text in the world. Therefore, DISTILLM-2 uses Teacher Outputs for SKL and Student Outputs for SRKL.

2. Curriculum Learning

The mixing coefficient \(\alpha\) in Skew KL is tricky to tune. If \(\alpha\) is too high, the student learns too slowly. If it’s too low, training becomes unstable.

DISTILLM-2 introduces an adaptive curriculum. It calculates a dynamic \(\alpha\) for each sample based on how “hard” it is (the gap between teacher and student probabilities).

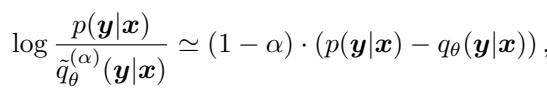
Using a first-order Taylor expansion (Mercator series), the authors derive a closed-form update for \(\alpha\). This allows the model to automatically adjust the “skewness” of the loss function. When the student and teacher are far apart (hard sample), \(\alpha\) increases to stabilize training. When they are close (easy sample), \(\alpha\) decreases to accelerate learning.

Additionally, the parameter \(\beta\) (which weights the student-generated penalty term) is linearly increased during training. This means the model focuses on imitation early on and self-correction later.

Experimental Results

Does this contrastive theory translate to real-world performance? The results suggest a resounding yes.

Instruction Following

The authors evaluated DISTILLM-2 on benchmarks like AlpacaEval and UltraFeedback using “LLM-as-a-Judge” (GPT-4).

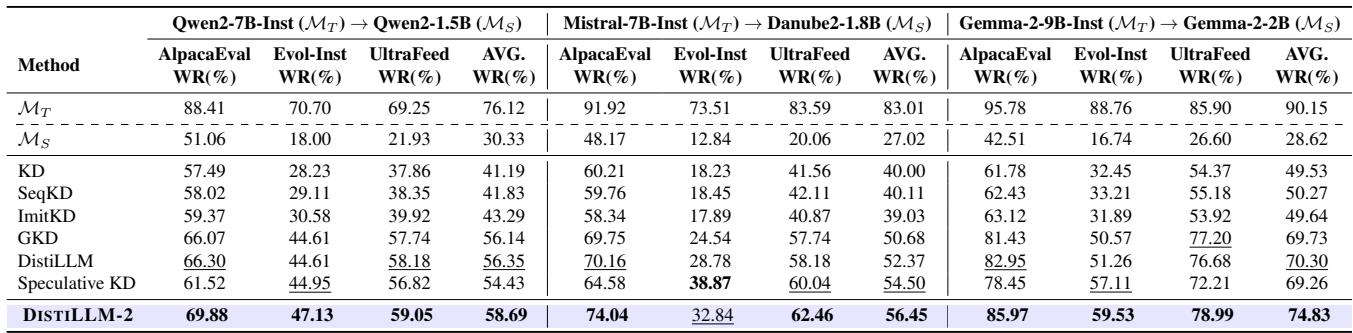
DISTILLM-2 consistently outperforms other distillation methods (like GKD, ImitKD, and standard DistiLLM). For example, with the Gemma-2 model, it achieves an 85.97% win rate on AlpacaEval, significantly higher than the previous state-of-the-art.

Math and Code Generation

Domain-specific tasks are notoriously hard for small models.

• Math (GSM8K & MATH): DISTILLM-2 helps a 1.5B parameter student outperform its own 7B teacher on the MATH benchmark (62.07% vs 67.07% average, but beating the teacher on specific metrics).

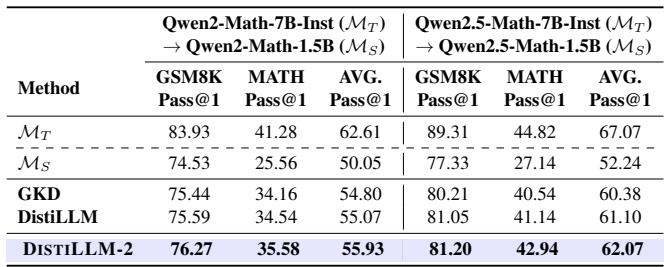
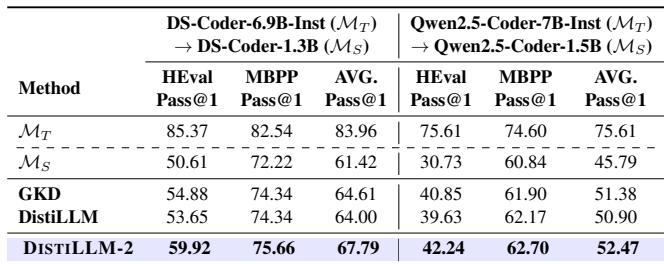
• Code (HumanEval & MBPP): In coding tasks, the method shows clear superiority over GKD and the original DistiLLM.

Component Analysis

Is the complexity worth it? An ablation study confirms that every piece of the puzzle contributes to the final score.

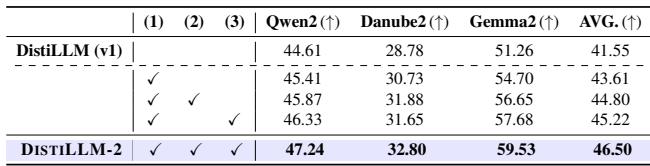
• Row 1: The base DistiLLM.
• Row 2: Adding the Contrastive Loss gives a boost.
• Row 3: Adding the dynamic \(\beta\) schedule helps further.
• Row 4: Adding the adaptive \(\alpha\) curriculum yields the final DISTILLM-2 performance.

Broader Applications

The paper demonstrates that DISTILLM-2 isn’t just for standard text generation. It has versatile applications in other areas of AI.

1. Preference Alignment: Before running Reinforcement Learning from Human Feedback (RLHF), models typically undergo Supervised Fine-Tuning (SFT). Replacing SFT with DISTILLM-2 creates a much better starting point (reference model), leading to better final alignment scores.

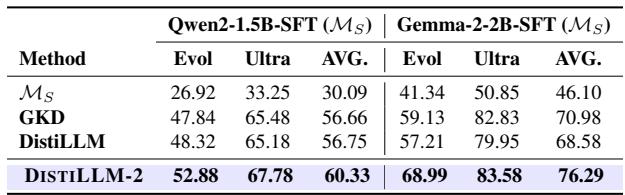
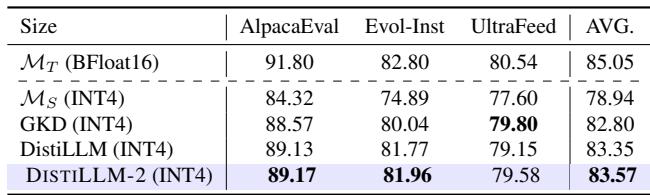
2. Vision-Language Models (VLMs): The method works across modalities. When distilling a large VLM (LLaVA-1.5-7B) into a smaller one, DISTILLM-2 achieved higher accuracy on visual question-answering benchmarks compared to other methods.

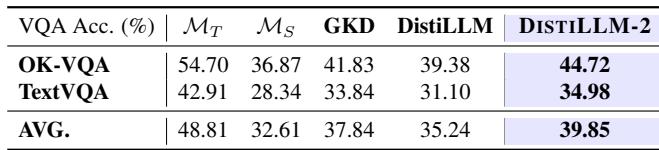
3. Rescuing Quantized Models: Quantization (reducing model precision to 4-bit) saves memory but hurts performance. DISTILLM-2 helps “heal” these quantized models, recovering lost accuracy more effectively than standard fine-tuning.

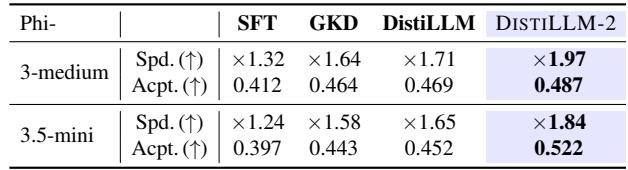
4. Faster Inference (Speculative Decoding): Speculative decoding uses a tiny “draft” model to guess tokens that a large model verifies. A better draft model means more accepted tokens and higher speed. Draft models trained with DISTILLM-2 yielded the highest speedups (up to 1.97x).

Conclusion

DISTILLM-2 represents a mature step forward in Knowledge Distillation. Instead of treating the student-teacher relationship as a simple imitation game, it acknowledges the asymmetry of the learning process.

By applying Skew KL to teacher data (to pull the student up) and Skew Reverse KL to student data (to push errors down), and managing this interplay with an adaptive curriculum, DISTILLM-2 allows small models to punch well above their weight class.

As AI deployment moves toward mobile devices and edge computing, techniques like DISTILLM-2 will be essential in bridging the gap between the massive intelligence of frontier models and the practical constraints of the real world.