Introduction

In the world of digital media, we are constantly fighting a battle between quality and size. We want crystal-clear 4K images, but we want them to load instantly and take up zero space on our phones. For decades, manually designed algorithms like JPEG, HEVC, and VTM have reigned supreme. But recently, a challenger has entered the arena: Neural Image Compression.

Neural codecs typically use deep learning to figure out how to squeeze image data better than any human-designed formula could. However, they come with a catch. They are often computationally heavy, requiring massive neural networks that drain battery life and slow down processors.

But what if we didn’t need to train a massive network from scratch? What if the perfect image compressor already exists inside a chaotic, randomly initialized neural network, and we just need to find it?

This is the premise behind LotteryCodec, a groundbreaking new method that challenges the status quo of image compression. By leveraging the “Lottery Ticket Hypothesis,” researchers have created a codec that uses untrained, random networks to achieve compression performance that beats the state-of-the-art classical codec (VTM) while remaining incredibly lightweight to decode.

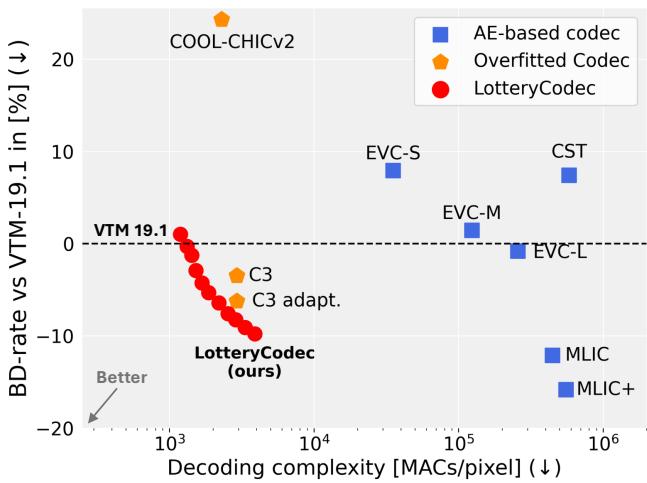
As shown in Figure 1, LotteryCodec (red circles) occupies a “sweet spot”: it offers better compression efficiency (lower BD-rate) while requiring significantly fewer operations (Decoding complexity) than other neural approaches.

In this post, we will unpack how this “winning ticket” works, how it encodes images into the structure of a random network, and why this might be the future of lightweight media on our devices.

Background: The Evolution of Neural Codecs

To understand why LotteryCodec is special, we need to look at how neural compression usually works.

The Two Main Approaches

Currently, there are two dominant paradigms in neural compression, as illustrated in Figure 3 below:

1. Autoencoder (AE)-based Codecs (Fig 3a): These are the heavy lifters. They consist of a massive Encoder and Decoder trained on millions of images. They are generalists—they know how to compress any image. However, because they are so large, running them on a mobile device is computationally expensive.
2. Overfitted Codecs (Fig 3b): This is a newer, fascinating approach. Instead of one general network, we train a tiny, specific neural network to memorize just one single image. We then transmit the weights of that tiny network. This is called an Implicit Neural Representation (INR).

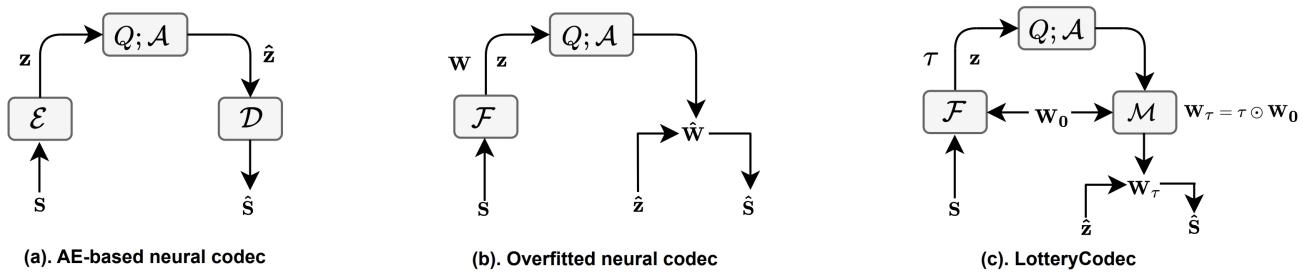
Standard overfitted codecs (like the method “COIN” or “COOL-CHIC”) are promising because the decoder is small. However, to get high-quality images, you typically need to make the network larger or train it longer, which bloats the file size because you have to transmit all those floating-point weights (parameters \(\mathbf{W}\)).

The Strong Lottery Ticket Hypothesis

LotteryCodec takes a third path (Fig 3c), inspired by a concept in machine learning called the Strong Lottery Ticket Hypothesis (SLTH).

The original Lottery Ticket Hypothesis stated that inside dense, trained neural networks, there exist sparse subnetworks (“winning tickets”) that can be trained in isolation to achieve similar performance. The Strong version takes this a step further: it suggests that if a randomly initialized network is large enough, it already contains a subnetwork that performs well without any weight training at all. You just need to prune away the “bad” connections.

This is the core insight of LotteryCodec: Don’t transmit weights. Transmit the architecture.

The Lottery Codec Hypothesis

The authors propose the Lottery Codec Hypothesis. It states that within a sufficiently large, random neural network, there exists a subnetwork that can act as a synthesis network for image compression, achieving performance comparable to a fully trained network.

Why does this matter?

1. Efficiency: We don’t need to transmit heavy 32-bit floating-point weights. We just need to transmit a binary mask (0s and 1s) that tells the decoder which connections to keep.
2. Priors: Randomly initialized networks actually capture natural image statistics surprisingly well (a concept known as the Deep Image Prior).

How LotteryCodec Works

The LotteryCodec system is an overfitted codec. This means for every image you want to compress, the system performs a search to find the best configuration for that specific image.

Here is the high-level workflow, visualized in Figure 2:

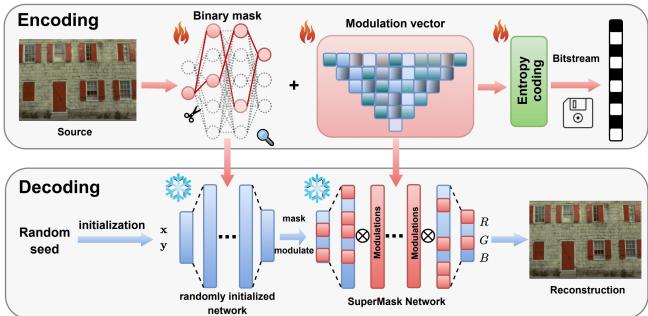
1. The Shared Random Network

Both the sender (encoder) and receiver (decoder) agree on a random seed. This seed is used to initialize a large, “over-parameterized” neural network. Because they share the seed, they generate the exact same random weights. No weights are ever transmitted.

2. Finding the “Winning Ticket” (The SuperMask)

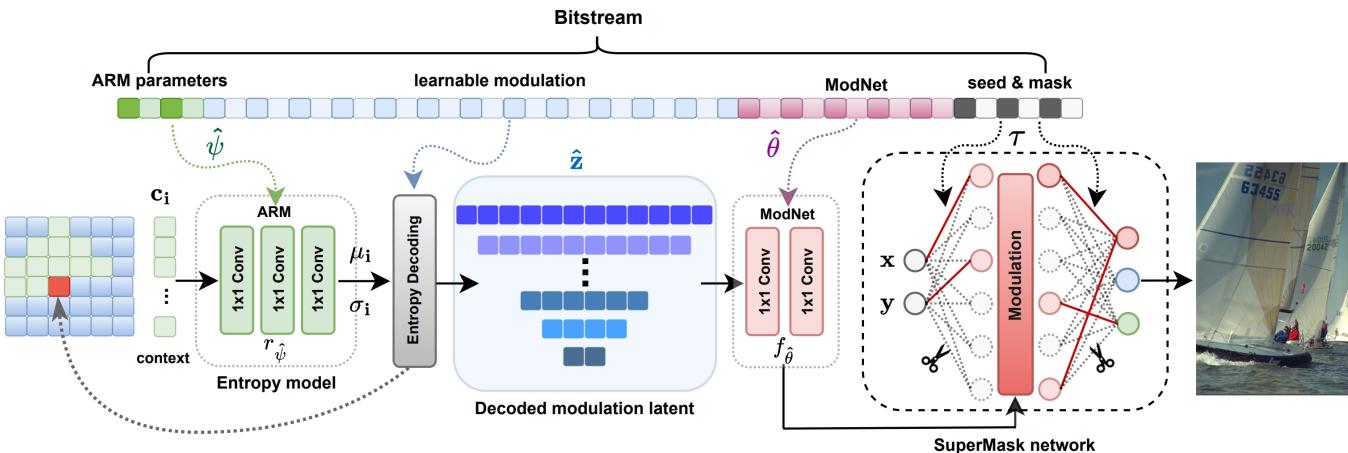
The encoder’s job is to find a subnetwork within this random mess that can reproduce the target image. It does this by learning a binary mask (\(\tau\)).

If a connection in the network helps recreate the image, the mask is set to 1. If it doesn’t, it’s 0. This process effectively “prunes” the random network into a specialized shape.

The mathematical operation for a layer in this “SuperMask Network” looks like this:

\[ v _ { k } ^ { ( i ) } = \sigma \left( \sum _ { j = 1 } ^ { d _ { i - 1 } } \tau _ { k , j } ^ { ( i - 1 ) } w _ { k j } ^ { ( i - 1 ) } m ( v _ { j } ^ { ( i - 1 ) } ) \right) , \]

Here, \(\tau\) is the learned mask, and \(w\) are the frozen random weights. Since \(\tau\) is binary, it is extremely cheap to compress and transmit compared to full weights.

3. Latent Modulations and ModNet

Simply pruning a random network isn’t quite enough to get photorealistic quality. The network needs guidance.

LotteryCodec inputs coordinate pairs \((x, y)\) to generate RGB pixels. But instead of just feeding raw coordinates, the authors introduce Latent Modulations. These are small, learnable vectors (\(\mathbf{z}\)) that provide high-level information about the image (like “this area is blue sky” or “this area is texture”).

These latents are processed by a small helper network called ModNet (Modulation Network). ModNet takes the compressed latent codes and generates modulation parameters that adjust the activations of the main random network.

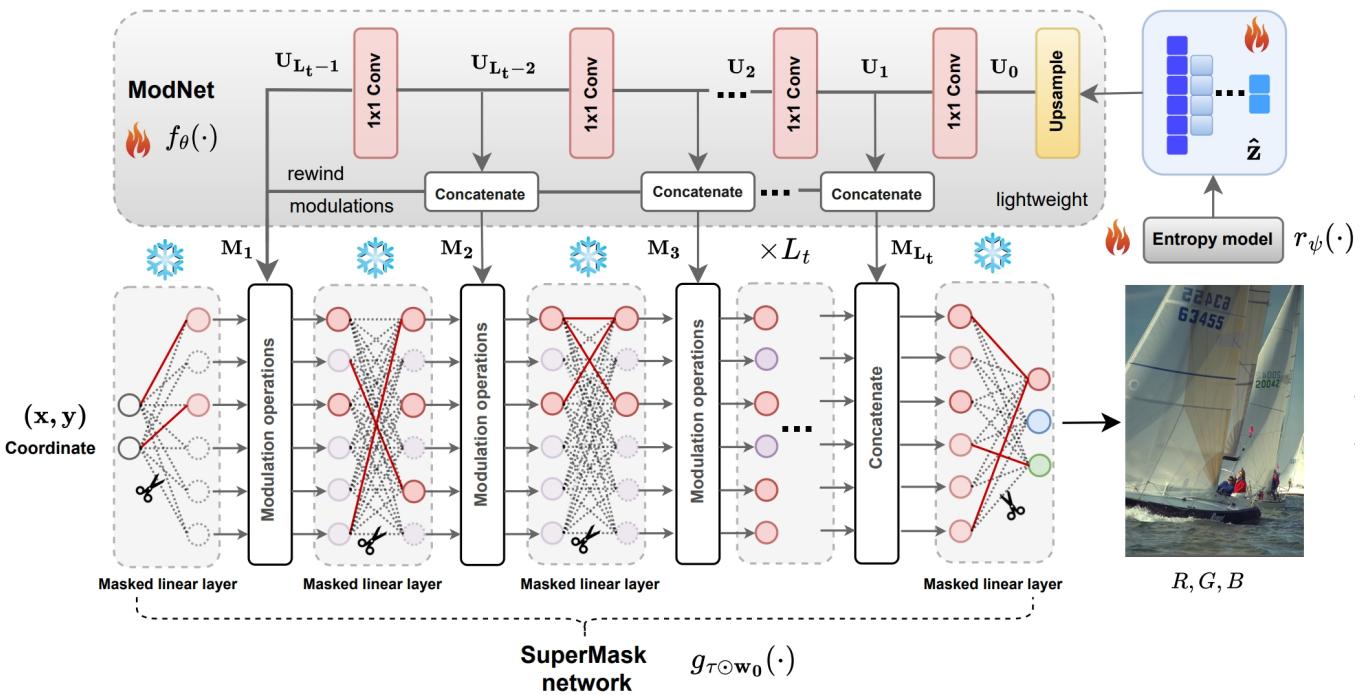
As seen in Figure 5, the SuperMask network (right) has frozen weights. The “winning ticket” is defined by the red solid lines (the mask). The ModNet (left) injects signal into this structure to steer the random weights toward the correct colors and shapes.

4. The “Rewind” Modulation Mechanism

One of the cleverest contributions of this paper is the Rewind Modulation.

In standard deep learning, information flows forward. However, searching for a subnetwork in a random graph is hard. To make it easier, the authors feed the features from the ModNet into the synthesis network in reverse order.

The deeper layers of ModNet (which contain coarse, high-level info) modulate the earlier layers of the synthesis network. The shallow layers of ModNet (fine details) modulate the deeper layers of the synthesis network. This “rewind” strategy enriches the random network with structural information, making it much easier to find a high-performing subnetwork.

The Decoding Process

The beauty of LotteryCodec lies in the decoding. It is exceptionally lightweight.

1. Initialize: The decoder generates the random network using the shared seed.
2. Configure: It applies the received binary mask \(\tau\), effectively deleting the useless connections.
3. Modulate: It decodes the small latent vectors \(\hat{z}\) and passes them through ModNet.
4. Synthesize: The masked random network processes the coordinates and modulations to produce the final image.

Because the mask makes the network sparse (removing 50-80% of connections), the decoder can skip most of the math. This results in the low “MACs/pixel” (multiply-accumulate operations) seen in the performance charts.

Experiments and Results

The researchers tested LotteryCodec on standard datasets (Kodak and CLIC2020) and compared it against the heavyweights of image compression.

Verification of the Hypothesis

First, they had to prove the hypothesis was real. Does a random network actually contain a good compressor?

Figure 6 confirms it. The charts show that if the random network is wide enough (over-parameterized), the “C3-Lottery” (a version of the codec using the lottery method) matches or beats the performance of a fully trained network (C3 baseline). This proves that training weights is not strictly necessary if the network is large enough to prune.

Rate-Distortion Performance

The ultimate test for any codec is the Rate-Distortion (RD) curve. You want to be as far to the top-left as possible (high quality, low bitrate).

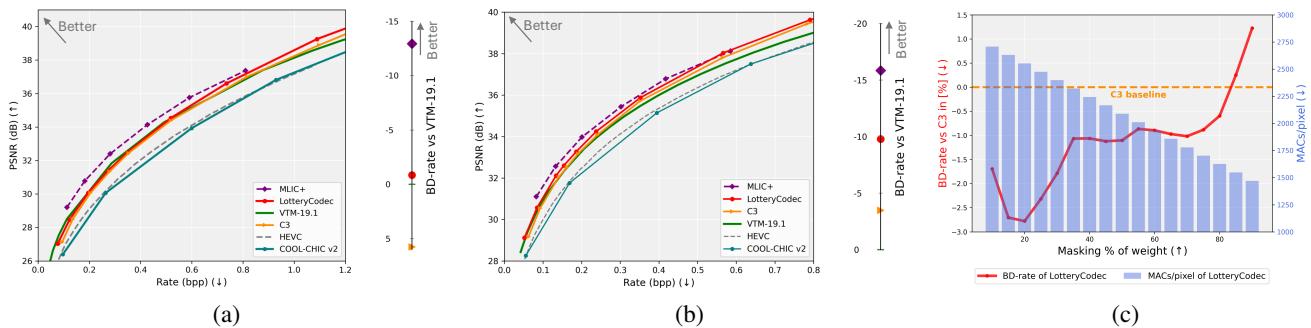
Figure 7 shows the results:

• Beating VTM: LotteryCodec outperforms VTM-19.1 (the reference software for the Versatile Video Coding standard). This is a massive achievement for an overfitted neural codec.
• Beating Neural Competitors: It significantly outperforms other overfitted codecs like C3 and COOL-CHIC.
• Low Bitrates: It shines particularly well at low bitrates because the binary mask is so efficient to store compared to floating-point weights.

Visual Quality

What do the “modulations” actually do? The visualization below shows how different latent vectors (\(\mathbf{z}\)) contribute to the final image.

In Figure 18, we can see that the latent codes (\(\mathbf{z}_1\) to \(\mathbf{z}_7\)) capture different frequencies. Some capture the overall shape (the lighthouse), while others fill in the fine textures. The system learns to balance these automatically.

Adaptive Complexity

One final advantage is flexibility. By changing the Mask Ratio (how many connections we prune), we can trade off quality for speed.

• High Mask Ratio (e.g., 90% pruned): Extremely fast decoding, slightly lower quality. Great for old phones or battery saving.
• Low Mask Ratio (e.g., 20% pruned): Maximum quality, slightly slower.

This allows LotteryCodec to adapt to the device it’s running on, a feature most static neural networks lack.

Conclusion

LotteryCodec represents a paradigm shift in neural image compression. It moves away from the idea that “intelligence” in a neural network comes solely from training the weights. Instead, it suggests that intelligence can be found in the structure of a random network.

By encoding an image into a binary mask and a set of modulations, LotteryCodec achieves:

1. State-of-the-Art Performance: Beating VTM and existing overfitted codecs.
2. Low Complexity: Sparse, masked networks are fast to run.
3. Adaptability: One codec can adjust its computational cost on the fly.

This work validates the “Lottery Codec Hypothesis” and opens the door for a new class of media formats that are efficient, powerful, and built on the surprisingly capable foundation of randomness. As we look toward a future of immersive video and AR/VR, lightweight decoding like this will be essential.

---