For nearly a decade, a ghost has haunted the halls of deep learning: the adversarial example. These are inputs—often images—that have been modified with tiny, human-imperceptible perturbations, yet they completely fool state-of-the-art neural networks. A picture of a panda, with a bit of finely tuned noise, suddenly becomes a gibbon to the machine’s eye.

This phenomenon isn’t just an academic curiosity—it poses a serious threat to AI systems deployed in safety-critical domains, from autonomous vehicles to medical diagnostics. Despite years of intense research, experts still debate why it happens. Are these vulnerabilities caused by flaws in our training methods, our architectures, or something more fundamental?

A recent paper, “Adversarial Examples Are Not Bugs, They Are Superposition,” offers an elegant and surprising explanation. The authors argue that adversarial examples are not a bug but an inevitable consequence of a trick neural networks use to be more efficient: superposition. Borrowed from mechanistic interpretability research, superposition is the idea that networks pack more concepts, or “features,” into their neurons than they have room for. This compression is powerful—but it comes at a cost: interference, a kind of internal crosstalk that adversarial attacks exploit.

Let’s unpack this hypothesis and explore the evidence, from simple toy models to large architectures like ResNet18.

Table showing six common adversarial phenomena and how the superposition hypothesis can explain each one.

Figure 1: Six persistent adversarial example phenomena and how superposition offers unified explanations—from their existence and noise-like appearance to transferability and interpretability effects.

What Is Superposition? A Crash Course

Before diving into the experiments, we need to grasp the idea of superposition. Mechanistic interpretability aims to reverse-engineer neural networks, unlocking the circuitry inside and treating them as understandable systems rather than black boxes. Within this framework, each neuron’s activation represents a direction in a high-dimensional space corresponding to a feature or concept the model has learned.

Imagine a single hidden layer’s activations \(h\) as a weighted sum of learned feature directions:

\[ h = \sum_{i < k} a_i \vec{f}_i + \vec{b} \]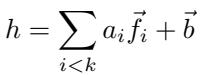

Equation showing a layer’s activations as a sum of feature vectors.

Equation 1: A layer’s activations as a linear combination of learned feature directions.

Here, \(k\) is the number of features the model attempts to represent, \(a_i\) is the strength of activation for feature \(i\), and \(\vec{f}_i\) is a vector in activation space representing that feature.

You might think that if this space has \(n\) dimensions, the layer could represent at most \(n\) distinct, orthogonal features—the network’s “capacity.” But remarkably, neural networks often represent many more features than they have neurons (\(k > n\)). How? By allowing these feature directions to overlap. This is called superposition.

Superposition is a form of representational compression. It lets models capture far richer structures than their size implies. However, overlapping features create interference: activating one feature partially activates others. Models learn to suppress this interference on typical data by tweaking bias terms, but in the worst case—such as in adversarial conditions—these suppressions fail.

An attacker can exploit this geometry by crafting inputs that co-activate hundreds of interfering features, generating large composite activations in the target feature. This is the heart of the hypothesis: adversarial attacks are coordinated exploitations of feature interference that arises from superposition.

To test whether superposition actually causes adversarial vulnerability, the authors turned to a simplified “toy model” where variables can be precisely controlled. Their setup consists of a small autoencoder that compresses 100 input features into a 20-dimensional hidden space and reconstructs them.

Manipulating Superposition: Sparsity as a Lever

When most input features are inactive (sparse inputs), the network learns overlapping representations—superposition—to use its limited hidden space efficiently. When inputs are dense, it learns clean, one-to-one mappings. Thus, by adjusting feature sparsity, the researchers can dial the amount of superposition up or down.

To measure superposition, they quantify “features per dimension”:

\[ \frac{\|W\|_F^2}{n} \]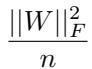

Equation for measuring features per dimension.

Equation 2: When this value exceeds 1, the model is representing more features than it has neurons—indicating active superposition.

To measure adversarial vulnerability, they generate \(L_2\)-bounded adversarial examples that maximize the reconstruction error:

\[ x_{adv} = x + \epsilon \cdot \arg \max_{\|\delta\|_2 \le 1} \mathcal{L}(x + \epsilon \delta) \]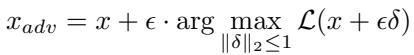

Equation for generating an L2-bounded adversarial example.

Equation 3: Construction of adversarial examples within a fixed perturbation budget \(\epsilon\).

Experiment 1: Superposition Controls Robustness

In their first experiment, the authors vary input sparsity to modify superposition and observe how vulnerability changes. The pattern is unmistakable: as sparsity increases, so does superposition—and adversarial vulnerability rises sharply.

Conclusion: Directly increasing superposition makes models more vulnerable. This provides the first causal evidence linking superposition to adversarial fragility.

Experiment 2: Robustness Controls Superposition

To establish bidirectional causality, the team flipped the question: if superposition causes vulnerability, can improving robustness reduce superposition?

They used adversarial training, mixing clean and attacked examples in the loss function:

\[ \mathcal{L}_{adv} = \alpha \cdot \mathcal{L}(x) + (1 - \alpha) \cdot \mathcal{L}(x_{adv}) \]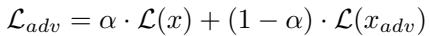

Equation for the adversarial training loss function.

Equation 4: Adversarial training objective balancing clean and robust performance.

The results were striking. As shown below, orange lines (adversarially trained models) consistently exhibit lower superposition and reduced vulnerability compared to blue lines (clean-trained models).

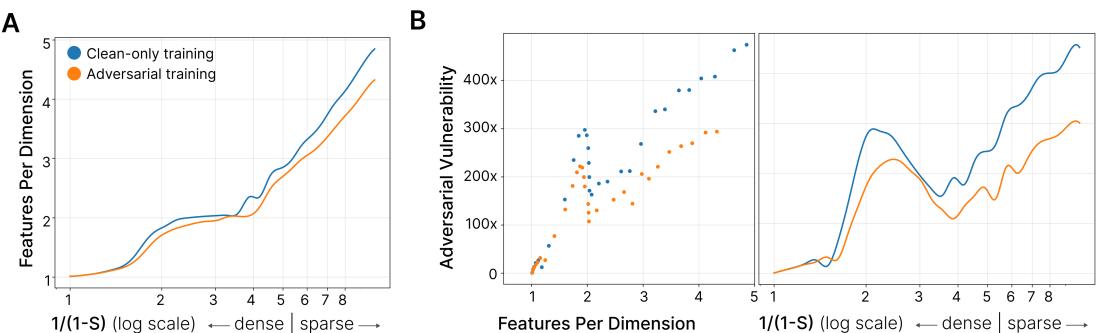
Two-panel figure comparing clean-trained (blue) and adversarially-trained (orange) models. Panel A shows that adversarial training reduces features per dimension. Panel B shows that vulnerability increases with superposition, and that adversarial training reduces vulnerability.

Figure 2: Adversarial training reduces both superposition and vulnerability. Clean-trained models show steep increases in adversarial vulnerability as superposition rises, while adversarially trained models maintain stability.

Adversarial training changes how networks optimize interference. Standard training minimizes average interference across the training distribution:

\[ \min_{\boldsymbol{\theta}} \mathbb{E}_{(x,y)\sim\mathcal{D}}[I(x,y;\boldsymbol{\theta})] \]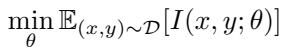

Equation for minimizing average interference during standard training.

Equation 5: Average-case interference minimization during standard training.

By contrast, adversarial training minimizes the worst-case interference across potential out-of-distribution examples:

\[ \min_{\theta} \max_{\mathcal{D} \in \mathcal{D}_{\text{OOD}}} \mathbb{E}_{(x,y)\sim\mathcal{D}}[I(x,y;\theta)] \]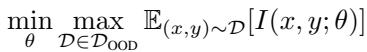

Equation for minimizing maximum interference during adversarial training.

Equation 6: Worst-case interference minimization under adversarial training.

This conceptual shift forces the network to prune overlapping—i.e., superposed—representations, producing more isolated, robust features.

Visualizing the Attack

To see superposition geometry in action, the authors visualized feature interference networks. Nodes represent features, and edge thickness corresponds to \((W_i \cdot W_j)^2\): how strongly features interfere.

Figure showing the superposition geometry of non-robust and robust models on clean and adversarial data. The non-robust model shows a massive increase in activated interfering features on adversarial data.

Figure 3: Adversarial attacks activate interfering features in superposition. Non-robust models display dense interference networks on adversarial data, while robust models maintain sparse, stable geometries.

In non-robust models, adversarial inputs activate sprawling networks of interfering features—proof that attacks exploit superposition geometry. Robust models, meanwhile, retain stable, clean feature relationships that resist perturbation.

Interestingly, adversarial training reduces superposition without destroying the geometric structure of features—it simply prunes overlapping directions.

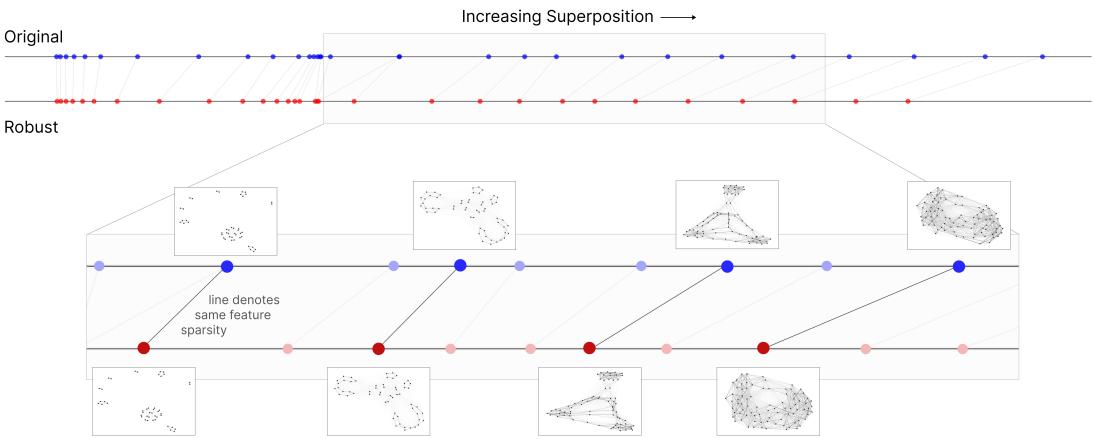
Figure showing that robust models have less superposition than original models trained on the same data, but the geometric structure is similar.

Figure 4: Robust models retain similar feature geometry while reducing superposition. Lines connect models trained at identical sparsity levels, showing consistent structures despite reduced overlap.

Evidence Part 2: From Toy Models to ResNet18

The toy model findings are powerful—but do they scale to complex, real-world networks?

In large models like ResNet18, we cannot directly measure or manipulate superposition since we don’t know the true feature basis. To bridge this gap, the researchers use Sparse Autoencoders (SAEs) trained on the internal activations of ResNet18.

SAEs are designed to decompose superposed features. If a model’s activations are heavily superposed, an SAE will struggle to reconstruct them, leading to higher loss. Thus, lower SAE reconstruction loss indicates less superposition.

Experiment 3: Robustness and SAE Loss in ResNet18

The authors trained SAEs on a series of ResNet18 models with varying degrees of adversarial robustness.

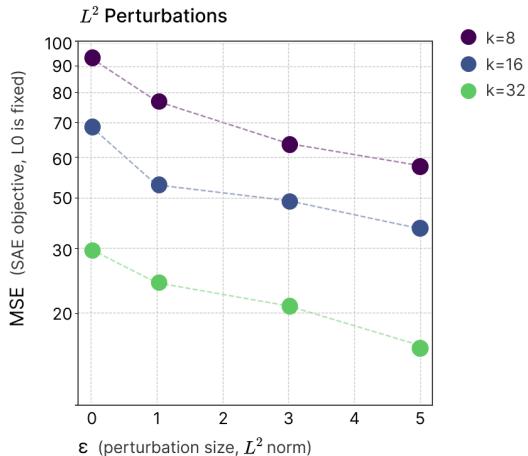
Line chart showing that more robust ResNet18 models (higher ε) achieve lower SAE reconstruction error (MSE), indicating less superposition.

Figure 5: Robust ResNet18 models yield lower SAE reconstruction loss. TopK SAEs across sparsity levels show systematic correlation between robustness (\(\epsilon\)) and reduced superposition.

More robust networks (trained on stronger attacks) consistently produce lower SAE reconstruction errors—mirroring the causal relationship seen in toy models. Adversarial robustness again corresponds to reduced superposition.

A Final Piece of Evidence: Attacks Increase Feature Activations

If adversarial examples exploit interference, they should trigger more features. Using SAEs, the authors measured how many features activated (the \(L_0\) norm) under different attack types.

Bar chart showing that adversarial attacks (FGSM and PGD) activate more features than clean inputs across the layers of a ResNet18.

Figure 6: Adversarial examples activate significantly more features than clean inputs. The iterative PGD attack spikes activation to nearly \(2.8\times\) baseline in deeper layers.

Adversarial attacks indeed cause more features to fire—particularly PGD, which activates nearly triple the number of features in the final layer. This layered amplification aligns perfectly with the idea that adversarial examples exploit compounded interference across successive superposed representations.

Conclusion: A Fundamental Trade-Off

Across both toy and real models, the evidence points to a profound truth: adversarial vulnerability and superposition are two sides of the same coin.

Superposition allows neural networks to be highly efficient, packing thousands of overlapping features into limited space. But this efficiency inherently creates channels of interference that adversaries can exploit. Adversarial training, by contrast, compels networks to untangle these overlaps, reducing superposition but also reducing representational efficiency.

This reveals a fundamental trade-off:

  • More superposition → greater efficiency and capacity.
  • Less superposition → greater robustness and interpretability.

In other words, making models safer could also make them more understandable. Both goals—robustness in the face of attacks and transparency in internal reasoning—may share the same path forward: reducing superposition.

As the paper’s title suggests, adversarial examples are not bugs—they are superposition.