Artificial intelligence has achieved remarkable feats—sometimes surpassing humans at complex reasoning, vision, and creative tasks. Yet most AI systems suffer from a fundamental weakness that humans mastered instinctively: learning continuously without forgetting.

When a neural network learns a new task, it’s prone to catastrophic forgetting: updating its weights for the new task erases the representations from past ones. Imagine learning to swim and suddenly forgetting how to ride a bike—that’s catastrophic forgetting in action. For AI meant to evolve over time, that’s a serious limitation.

This challenge is especially acute for generative models—the engines behind image synthesis, text generation, and art creation—because these models must retain creative diversity across many concepts. Retraining them from scratch for every new domain is expensive and slow. Traditional “rehearsal” approaches, which retrain on mixtures of old and new synthetic data, only postpone the inevitable. Over time, their accuracy and fidelity degrade—a bit like photocopying a photocopy.

A recent research paper, Deep Generative Continual Learning using Functional LoRA (FunLoRA) by Victor Enescu and Hichem Sahbi, introduces a sleek and surprisingly simple mechanism that tackles this head‑on. FunLoRA lets AI models learn sequentially without forgetting, all while using a tiny number of additional parameters. It revisits a known fine‑tuning strategy, LoRA, and gives it a functional twist—one that could fundamentally shift how generative models learn over time.

Background: Why Continual Learning Is So Hard

Continual Learning (CL) aims to train a model across a stream of tasks without losing information from previous ones. For discriminative classifiers, the challenge is keeping past decision boundaries stable; for generative models, it’s even tougher—they must still reproduce all past data distributions reliably.

Early solutions like exemplar replay stored old data or synthetic samples, but that approach has heavy memory and privacy costs. More advanced solutions rely on generative replay—where the model retrains on data it generates itself—but this leads to slow convergence and steadily declining quality.

FunLoRA sidesteps all these pitfalls by rethinking how models acquire new capabilities.

Flow Matching: A Simpler, Faster Generative Process

Most modern generative models—such as Stable Diffusion—are built around diffusion: a process that adds noise to data and learns to reverse it through hundreds of denoising steps. This produces top‑quality results but is painfully slow.

FunLoRA instead builds upon Conditional Flow Matching (CFM), a faster and more direct generative technique. It learns a vector field \(v_{\theta}(t, \mathbf{x})\) that smoothly maps a noise vector to a real image, bypassing the need for iterative noise removal.

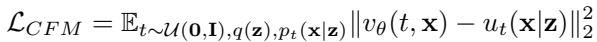
Illustration of the Conditional Flow Matching loss function.

The model learns to align its predicted velocity field \(v_{\theta}\) with a known conditional target field \(u_t(\mathbf{x}|\mathbf{z})\).

The probability path between noise and data is simply:

\[ \mathbf{x} = (1 - t)\mathbf{x}_0 + t\mathbf{z} \]

The straight probability path used in flow matching.

Flow matching uses a direct linear interpolation between data and noise, unlike diffusion’s curved multi‑step paths.

This “straight path” formulation makes sampling fast and tractable—perfect for continual learning settings where large numbers of images must be generated efficiently.

LoRA: The Efficient Way to Fine‑Tune Models

Large neural networks can contain billions of parameters, making full fine‑tuning wasteful and computationally costly. Low‑Rank Adaptation (LoRA) solves this by keeping most weights frozen and learning small low‑rank perturbations.

Instead of updating the full weight matrix \(\mathbf{W}_0\), LoRA learns a residual \(\Delta \mathbf{W}\) as the product of two thin matrices \(\mathbf{A}\) and \(\mathbf{B}\):

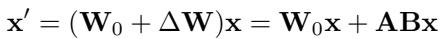
The standard LoRA update mechanism.

LoRA expresses the update as \(\Delta \mathbf{W} = \mathbf{A}\mathbf{B}\). The total number of learnable parameters drops drastically.

During inference, both the base weights and their low‑rank correction are used. This technique has transformed how massive language and vision models adapt efficiently—especially when data are scarce.

FunLoRA: Functionally Expanding Expressiveness

Traditional LoRA is powerful but still suffers from one limitation: expressiveness depends on rank. A rank‑1 matrix (the most compact form) can only express linear relations—it’s frugal but weak. FunLoRA solves this by functionally increasing rank through clever mathematical transformations.

1. LoRA for Convolutional Layers

While standard LoRA targets attention layers in Transformers, the U‑Net architecture—central to many generative models—processes class and time information mainly through convolutions. FunLoRA thus applies LoRA directly to these layers.

For each class label \(y\):

\[ \mathbf{F}_y = \mathbf{A}_y \mathbf{B}_y \]

where \(\mathbf{A}_y\) and \(\mathbf{B}_y\) are rank‑1 matrices reshaped to match convolutional filter dimensions.

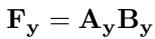
Learned LoRA reparameterization applied to convolutional filters.

Each class learns a pair of vectors, whose product forms \(\mathbf{F}_y\), the modulation matrix for its convolutional filters.

Instead of adding this update to \(\mathbf{W}_0\), FunLoRA multiplies element‑wise:

\[ \mathbf{W}_y = \mathbf{W}_0 \odot \mathbf{F}_y \]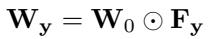

Modulating convolutional weights with the learned matrix \\(F_y\\).

The Hadamard (element‑wise) product rescales filters according to class‑specific function matrices, preserving the original backbone.

This approach yields a unique sub‑network per class without duplicating the entire model—ensuring no interference between tasks and no forgetting.

2. Functionally Increasing Rank

The real innovation is how FunLoRA boosts rank without adding parameters. It applies a set of \(p\) functions \(f_i\) to \(\mathbf{A}_y\) and \(\mathbf{B}_y\), then averages their outputs:

\[ \mathbf{F}_y = \frac{1}{p}\sum_{i=1}^{p}\alpha_i f_i(\mathbf{A}_y,\mathbf{B}_y) \]

Combining multiple functions to form the final FunLoRA matrix.

Different nonlinear functions \(f_i\) enrich the expressiveness of \(\mathbf{F}_y\) without increasing parameter count.

The functions can include:

  • Circular Shifts: shifting vector elements before multiplication.
  • Element‑wise Powers: applying powers like \(x^1, x^2, \ldots, x^p\).
  • Trigonometric Functions: using cosine waves at distinct frequencies.

Among them, trigonometric functions proved most effective. The cosine variant:

\[ f_i^{\cos}(x) = \cos(\omega_i x) \]

learns distinct frequencies \(\omega_i\) with trainable importance weights \(\alpha_i\), enabling expressive periodic modulations that mimic higher‑rank transformations.

The cosine function used in FunLoRA, with learnable frequencies \\(\\omega_i\\).

Cosine functions expand and diversify the effective rank by introducing frequency-based variation.

Applied throughout the U‑Net, this mechanism dynamically conditions convolutional layers for each class.

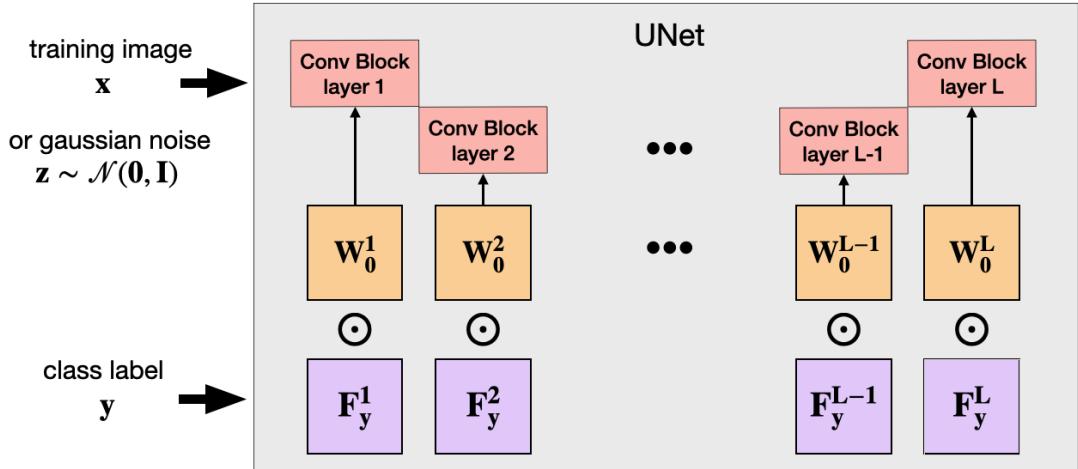
Visualization of U‑Net architecture with class-conditional functional matrices.

Convolutional blocks are adapted using functional matrices \(\mathbf{F}_y^l\) across encoder and decoder paths.

Experiments: Does FunLoRA Deliver?

FunLoRA was tested on popular continual learning benchmarks—CIFAR10, CIFAR100, and ImageNet100—each split into sequential tasks where new classes are introduced over time.

Identifying Critical Layers

Not all layers contribute equally to adaptation. The authors measured an importance score (based on parameter deviation) for each convolutional layer.

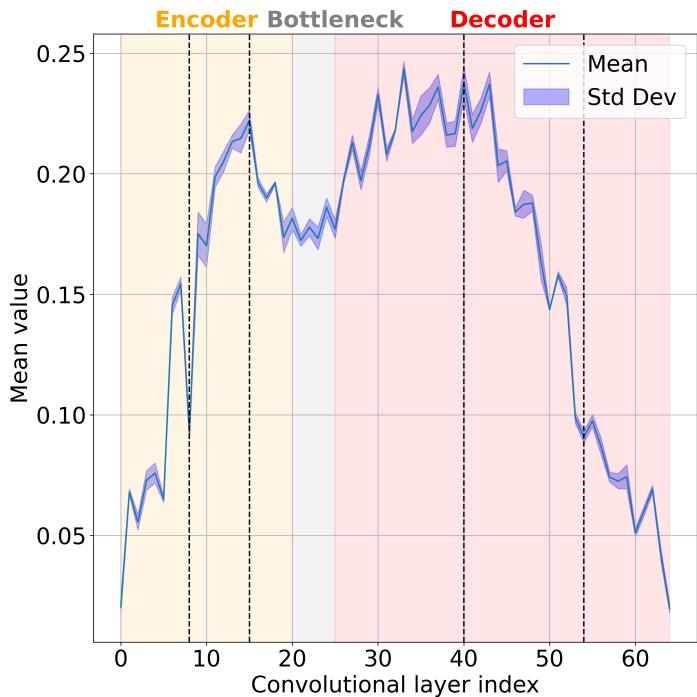
Importance of convolutional layers across the U‑Net.

Middle and decoder layers show the highest importance values—making them prime candidates for LoRA adaptation.

Focusing only on layers with indices 40–54 slashed parameter count by threefold, with merely two accuracy points lost. This revealed that mid‑level decoder layers are core to class adaptation.

Ablation Studies: The Power of Cosine

In comprehensive ablations, cosine‑based functional expansion ranked highest across metrics. It beat traditional LoRA addition and multiplication baselines—even those using more parameters.

Function UsedLayers IndexParameters per Class ↓Last Accuracy ↑Avg. Incremental Accuracy ↑
Vanilla (Add)0–6435.59K59.2367.17
Vanilla (Mul)0–6435.59K60.8468.82
Cosine (Learnable)0–6435.35K61.8269.18
Vanilla (Add)40–5411.26K59.2967.65
Cosine (Learnable)40–5410.03K60.0768.06

Across all datasets, the cosine variant achieved the best performance while remaining extremely memory‑efficient.

Intuitively, cosine’s oscillatory nature gives the model flexible, localized expressiveness. Its effective rank often exceeded the number of functions applied (\(p = 10\)), surpassing limits seen with power or shift functions.

Effective rank of FunLoRA matrices during training and across layers.

Cosine-based functions reach maximal ranks beyond \(p=10\), yielding richer transformations.

Further analysis revealed how learned ponderations \(\alpha_i\) and frequencies \(\omega_i\) varied across layers—early layers emphasizing mid frequencies for class discrimination, and later ones focusing on low frequencies for global structure.

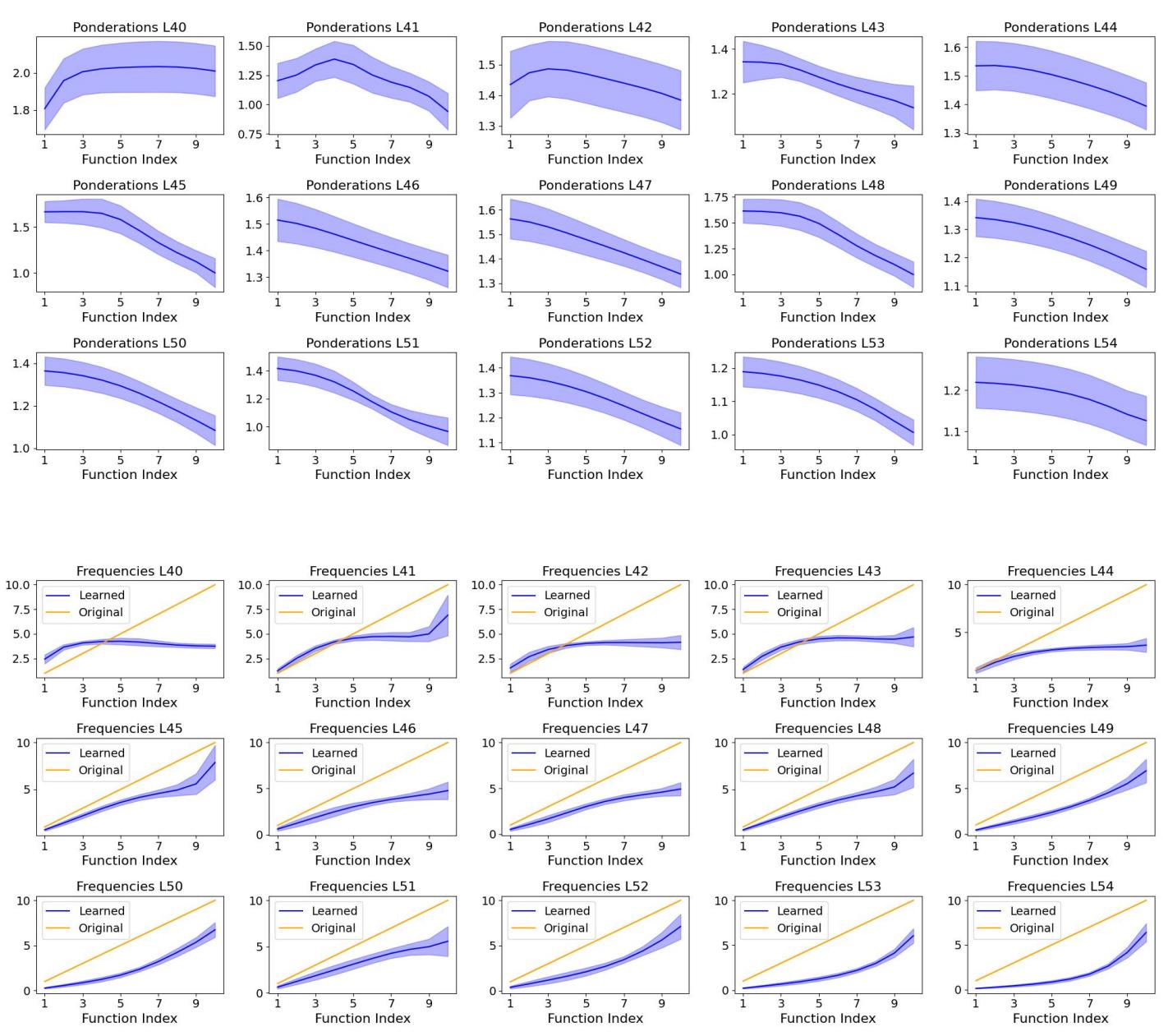
Learned ponderations \\(\\alpha_i\\) and frequencies \\(\\omega_i\\) across layers.

Low-frequency functions dominate in output layers, while middle layers capture complex conditional patterns.

Standing Against the State of the Art

Finally, FunLoRA was benchmarked against top continual generative methods—DDGR, GUIDE, JDCL, DiffClass—and variants using massive pretrained models.

MethodCIFAR100 LA↑ImageNet100 LA↑Backbone Params
DDGR (Diffusion)28.1125.5952.4M / 295M
GUIDE41.6639.0752.4M / 295M
JDCL47.9554.5352.4M / 295M
DiffClass (Stable Diffusion, pretrained)62.2167.26983M
FunLoRA (ours)60.0758.3036.6M / 90.7M
FunLoRA + Resample67.8963.0336.6M / 90.7M

FunLoRA surpasses highly trained diffusion alternatives despite being smaller, faster, and retrained from scratch.

Remarkably, the “Resample” variant of FunLoRA, which generates additional synthetic data, even outperforms DiffClass—a method using a 983‑million‑parameter pretrained Stable Diffusion model—on CIFAR100. This demonstrates that continual generative learning can be both compact and powerful.

Qualitative comparisons drive the point home.

ImageNet100 samples: FunLoRA (left) vs. multi-task training (right).

Visual samples look virtually identical between incremental and multi‑task training.

CIFAR100 samples: FunLoRA (left) vs. multi-task upper bound (right).

Incrementally trained FunLoRA preserves image quality perfectly, confirming no catastrophic forgetting.

Why FunLoRA Matters

The FunLoRA framework redefines efficiency for continual generative learning:

  • No Forgetting: Each class uses independent adaptive parameters—no interference between old and new tasks.
  • Tiny Parameter Cost: Only a handful of extra parameters per class; scaling remains practical even for thousands of tasks.
  • High Expressiveness: Functional rank boosting (especially with cosine functions) approximates rich transformations with minimal memory.
  • Speed: Flow‑matching training and sampling outperform diffusion models by orders of magnitude, enabling real‑time adaptation.

FunLoRA illustrates that continual learning doesn’t need large pretrained models or heavy replay schedules. With thoughtful functional design, even rank‑1 structures can evolve dynamically into expressive, lifelong learners.

In Summary

FunLoRA is more than an optimization trick—it’s a new way to think about neural adaptability. By fusing flow matching’s speed with LoRA’s parameter efficiency and adding a layer of functional creativity, it achieves something long hoped for in AI:

An intelligent system that keeps learning—forever—without ever forgetting what it knows.

This marks a key step toward true lifelong learning for generative AI.