Beyond Right and Wrong: Teaching LLMs to Judge Their Own Confidence

Large Language Models (LLMs) are astonishingly capable—but also dangerously confident. When an LLM generates a flawless-sounding medical diagnosis or legal analysis that is completely wrong, the problem isn’t just accuracy, it’s misplaced certainty. In high-stakes domains, uncalibrated confidence turns mistakes into risks.

To make LLMs truly trustworthy partners, they need a sense of their own uncertainty. In other words, when a model says it’s 90% confident, that should mean it’s actually right about 90% of the time. Achieving this alignment is known as confidence calibration—and it’s one of the hardest problems in AI safety.

A recent study by researchers from HKUST, “CritiCal: Can Critique Help LLM Uncertainty or Confidence Calibration?”, proposes an intriguing solution. Instead of trying to guess the correct confidence numbers, what if we teach models to critique their own reasoning—to understand why their confidence might be misplaced? Their method, called CritiCal, uses natural language critiques to fine-tune an LLM’s ability to express calibrated confidence. Remarkably, models trained with CritiCal can even outperform their own teacher, GPT‑4o.

Let’s explore how CritiCal works and what it tells us about making LLMs not just smarter—but more self‑aware.

Understanding the Calibration Challenge

Traditional calibration methods fall into two camps:

1. White‑Box Methods: These extract internal signals from a model—such as token probabilities or hidden states—to infer how sure it is. While precise, these require access to the model’s internals, which is impossible for closed‑source APIs.

2. Black‑Box Methods: These rely only on output behavior. Common examples include consistency‑based sampling, where multiple queries test response stability, or verbalization‑based training, which explicitly teaches models to express confidence (e.g., “The answer is Paris, and my confidence is 95%”).

The problem is that these strategies largely teach models to imitate confident expressions rather than genuinely reason about certainty. To fix that, the HKUST researchers turned to critiques—natural language feedback explaining why an answer or the reasoning behind it is wrong or uncertain.

Critiques have been used before to improve factual accuracy, but this is the first systematic attempt to use them for confidence calibration.

What to Critique: Uncertainty vs. Confidence

The study begins by tackling a deceptively simple question: should we critique uncertainty or confidence?

• Uncertainty refers to doubt about the question itself (“How hard or ambiguous is this?”).
• Confidence refers to assurance in the specific answer produced (“How sure am I this particular answer is right?”).

To test which works better, the researchers prompted five different LLMs across six benchmarks to verbalize either uncertainty or confidence.

Figure 1: Mean Expected Calibration Error (ECE ↓) and AUROC (↑) across open-ended and multiple-choice tasks. Uncertainty performs better on open‑ended tasks, while confidence dominates in multiple‑choice settings.

For open‑ended tasks—like TriviaQA or MATH—uncertainty leads to better calibration. The open-ended nature means the space of possible answers is vast, so uncertainty about the question correlates naturally with performance.

For multiple‑choice tasks, confidence statements are more effective. LLMs can eliminate alternatives and express more accurate certainty about one specific choice.

Key takeaway:

• For open‑ended reasoning—critique uncertainty.
• For structured multiple‑choice questions—critique confidence.

How to Critique: Self‑Critique vs. CritiCal

Having uncovered what to critique, the researchers next asked how. Can a model critique itself effectively, or is external guidance required?

They compared two approaches:

1. Self‑Critique — Reflection by Prompting

In Self‑Critique, a model re‑examines its own answers through iterative prompting. Each round asks the LLM to reconsider ambiguities and logical gaps, then refine its confidence score.

Unfortunately, performance was inconsistent across models and tasks.

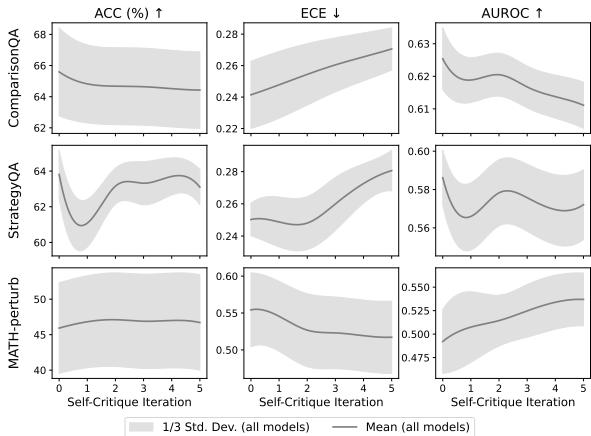
Figure 2: Multi‑turn Self‑Critique results. Accuracy slightly drops, while calibration error (ECE) tends to worsen with each round.

Self‑Critique rarely improved calibration—and sometimes made it worse. For factual reasoning tasks, ECE rose, meaning confidence drifted further from correctness.

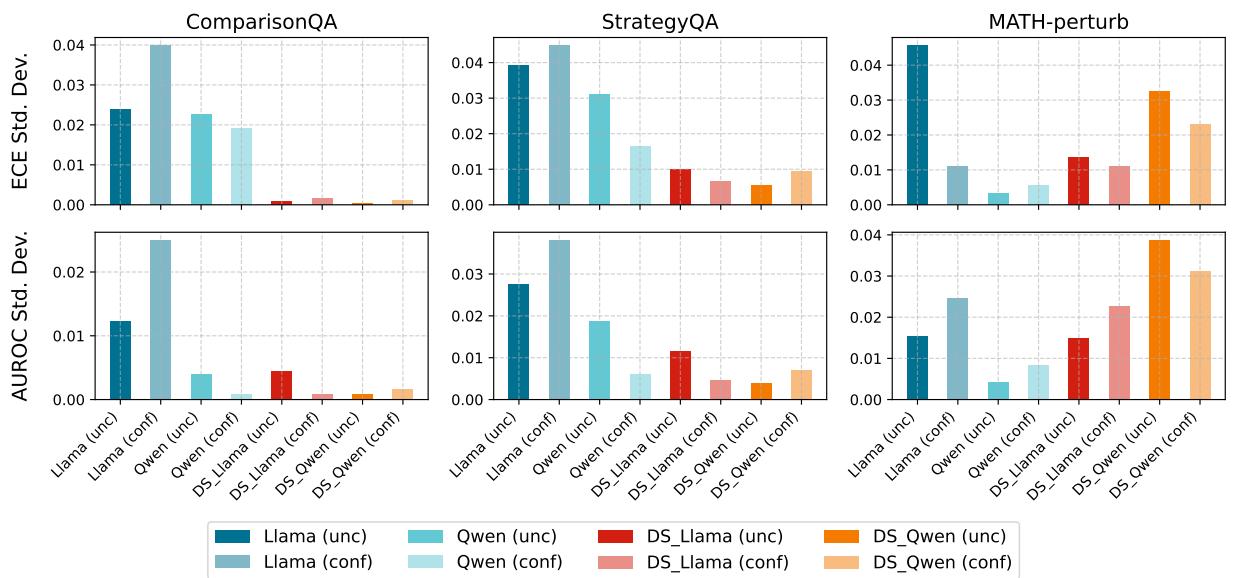
Figure 3: Variability across 6 rounds of Self‑Critique. Large reasoning models (LRMs, warm colors) are more stable, but gains remain minor.

Models showed different—and often opposite—trends.

Figure 4: Average uncertainty and confidence during Self‑Critique. Llama grows more uncertain; Qwen grows more confident—revealing inconsistent biases.

In short: Self‑Critique lacks the objective grounding needed for reliable improvement. Without external feedback, models reinforce their own tendencies rather than correcting them.

2. CritiCal — Supervised Critique Calibration

To overcome these issues, the researchers developed CritiCal, a supervised fine‑tuning (SFT) method that trains a model to learn confidence calibration through external critiques.

Figure 5: Traditional calibration vs. CritiCal. CritiCal replaces numeric labels with explanatory critiques, teaching models to reason about confidence quality.

Here’s the process:

1. Student Response Generation: A smaller “student” model answers questions and provides a verbalized confidence score.
2. Teacher Critique Generation: A larger “teacher” model—GPT‑4o—reviews the student’s output alongside the correct answer. It then produces a natural‑language critique evaluating the student’s confidence.
3. Fine‑Tuning on Critiques: The student is fine‑tuned to generate similar critique outputs.

Instead of memorizing target confidence numbers, the student now learns to connect reasoning strength and correctness to confidence level—absorbing how to judge adequacy of its own reasoning.

Experiments: Testing CritiCal

The authors benchmarked CritiCal against several baselines:

• Vanilla prompting
• Self‑Critique
• SFT‑Hard (training with rigid 0%/100% confidence labels)
• SFT‑Soft (training with soft 20%/80% labels)

All tests used datasets spanning factual, reasoning, and math‑intensive tasks.

In‑Distribution Accuracy

CritiCal consistently produced the lowest calibration error (ECE) and highest AUROC values on complex reasoning tasks.

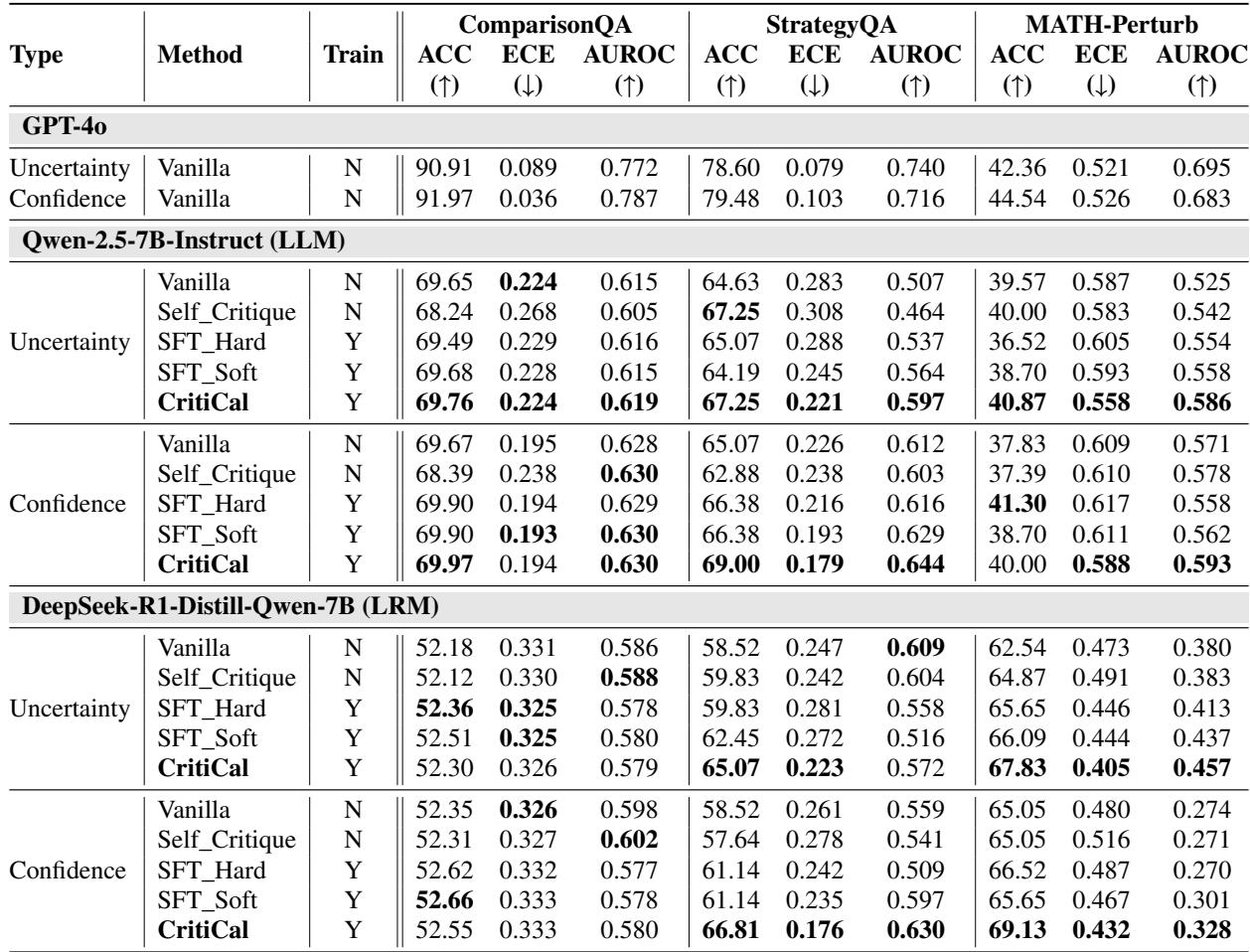
Table 1: In‑distribution performance across three benchmarks. CritiCal achieves best calibration on StrategyQA and MATH‑Perturb.

The most fascinating finding: A student trained via CritiCal sometimes surpassed its teacher.

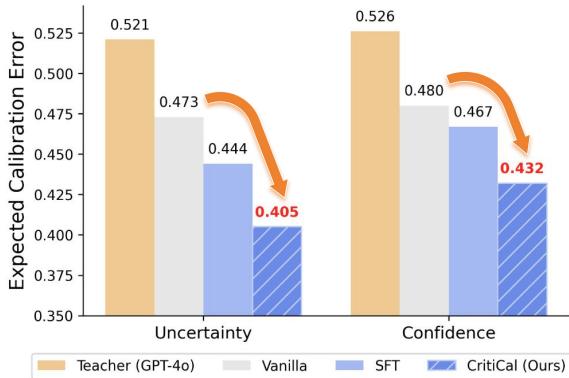
Figure 6: MATH‑Perturb results. CritiCal (dark blue) outperforms vanilla, SFT, and even its teacher GPT‑4o (orange).

This striking result shows that critique‑based learning can transfer not only skills but also judgment quality. The student internalizes calibration principles that help it exceed the calibration accuracy of the teacher.

Out‑of‑Distribution Generalization

Next, the experiment tested how well CritiCal transfers across domains. Models trained on multi‑hop reasoning (StrategyQA) were tested on math reasoning (MATH‑Perturb).

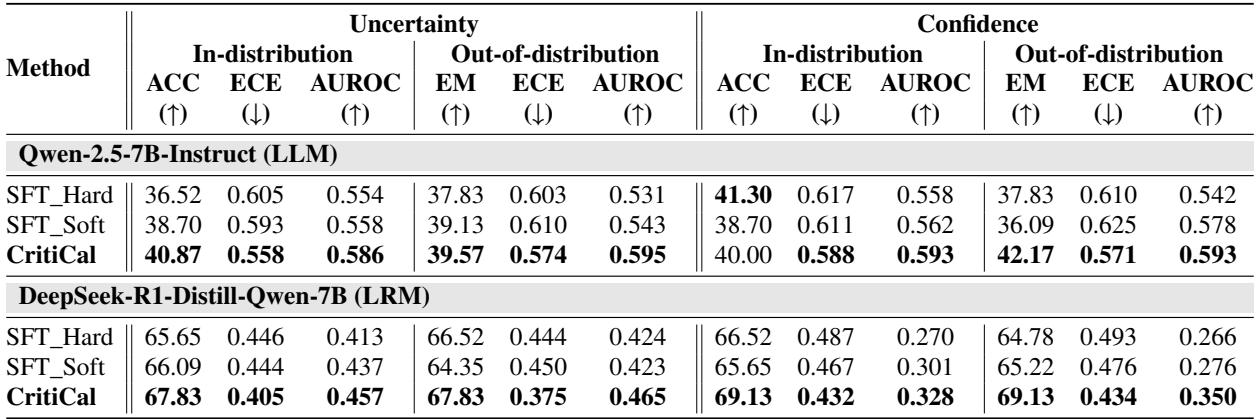
Table 2: Generalization from StrategyQA to MATH‑Perturb. CritiCal maintains or improves calibration, while standard SFT degrades.

While both hard and soft SFT collapsed on unseen tasks, CritiCal’s performance actually improved. The critiques helped models learn generalizable reasoning signals, not dataset‑specific patterns.

Which Training Method Works Best: SFT or DPO?

The team also tested Direct Preference Optimization (DPO)—a reinforcement‑style fine‑tuning—against SFT for training CritiCal.

Table 3: SFT vs. DPO for CritiCal. Near‑identical results; SFT is preferred for efficiency.

DPO gave comparable results but required substantially more computation. Thus, SFT provides an efficient and sufficient training method for CritiCal.

Why CritiCal Matters

CritiCal doesn’t just tweak confidence scores—it teaches models to judge the appropriateness of their own certainty. This shift makes calibration more interpretable, stable, and transferable.

Key insights emerging from the work:

• Different tasks require different critique targets. Calibrate uncertainty for open‑ended reasoning; confidence for multiple‑choice.
• Self‑reflection alone isn’t enough. Without external critique, models reinforce internal biases.
• Critiques enable structured self‑knowledge. By learning teacher critiques, student models gain contextual understanding of reasoning strength.
• Critique‑trained models generalize—and even surpass their teachers. A properly designed critique signal can outperform direct numeric optimization.

Conclusion: Toward Self‑Aware AI

The CritiCal framework marks a critical step toward dependable AI systems. It flips calibration from a numeric guessing game to a process of linguistic reasoning—helping models understand the relationship between logic, correctness, and certainty.

An LLM that knows when its footing is shaky—and can explain why—is infinitely more useful than one that confidently asserts falsehoods. As critique‑based training spreads, it will help transform LLMs from persuasive talkers into trustworthy collaborators, capable of signaling when users should take their words with caution.

CritiCal reminds us that in AI safety, self‑knowledge is just as important as intelligence.