Beyond the Right Answer: A Deep Dive into IMO-Bench, the New Gold Standard for AI Math

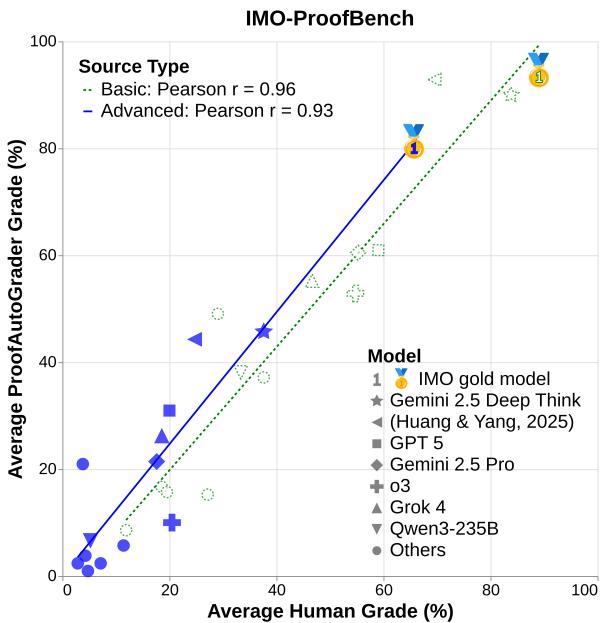
Figure 1 | Correlation between human and automatic grading on IMO-ProofBench. Both basic and advanced problems show strong alignment, signaling the viability of automated proof evaluation.

The race to build smarter AI systems has seen large language models (LLMs) make incredible strides in mathematical reasoning. Early benchmarks like GSM8K and MATH once set the standard for challenge, but these datasets are now nearing saturation. Many top models can breeze through them, leaving researchers to wonder whether they measure true reasoning or just pattern recognition.

The deeper issue is that most math benchmarks only check final answers. It’s a bit like grading a calculus exam by looking solely at the boxed number at the end, ignoring all the derivations that got you there. That might capture guesswork, not genuine reasoning.

To push the field forward, we need a tougher challenge—one that values the process as much as the result. Enter IMO-Bench, introduced in the paper “Towards Robust Mathematical Reasoning”. The research team behind it turned to the toughest arena for young mathematicians: the International Mathematical Olympiad (IMO).

The IMO isn’t about rote computation. Its problems are designed to test ingenuity, creativity, and proof-writing skills. By building AI benchmarks at that level, the authors aim to shift the spotlight from “getting it right” to “proving it right.” This article takes a deep dive into the three components of IMO-Bench, explores how the world’s leading AI models performed, and discusses how this benchmark marks a turning point for reliable, verifiable reasoning in AI.

Why the International Mathematical Olympiad?

Before exploring the benchmarks themselves, it’s worth asking why the IMO is an ideal foundation for AI reasoning tests.

Unlike many datasets, which focus on formulaic problem solving or memorization, IMO problems require invention. They often involve combining concepts from diverse fields—algebra, geometry, number theory, combinatorics—and inventing novel steps never explicitly taught before. The goal isn’t just computation; it’s creative logic under pressure.

That’s exactly what makes it an excellent test bed for robust reasoning. To construct IMO-Bench, the authors collaborated with a panel of IMO medalists who vetted problems and designed grading standards to ensure rigor, fairness, and difficulty.

The IMO-Bench suite is composed of three distinct benchmarks, each targeting a unique aspect of reasoning.

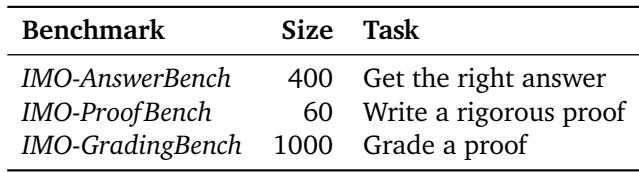
Table 1 | The three pillars of IMO-Bench: short-answer accuracy, proof-writing skill, and grading capability.

Part 1: IMO-AnswerBench — Can Models Find the Right Answer?

The first component, IMO-AnswerBench, contains 400 Olympiad-style problems with short, verifiable answers. This stage assesses a model’s ability to compute precise results under Olympiad-level reasoning without explicit proofs.

Problem Selection and Diversity

The problems span the four classic pillars of competition mathematics—Algebra, Combinatorics, Geometry, and Number Theory—each contributing 100 examples. Difficulty levels range from middle-school pre-IMO questions to genuine IMO problem #3 or #6–level challenges.

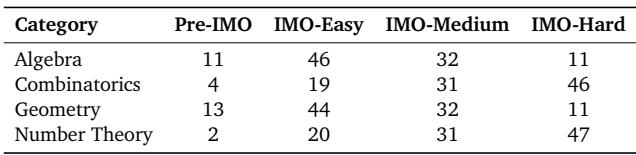
Table 2 | Difficulty distribution across mathematical domains in IMO-AnswerBench.

This diversity ensures the benchmark reflects not just computation but conceptual breadth. As shown below, topic distributions vary widely across fields. Geometry tends to emphasize angle and side-length computation, while Number Theory and Combinatorics explore complex reasoning patterns.

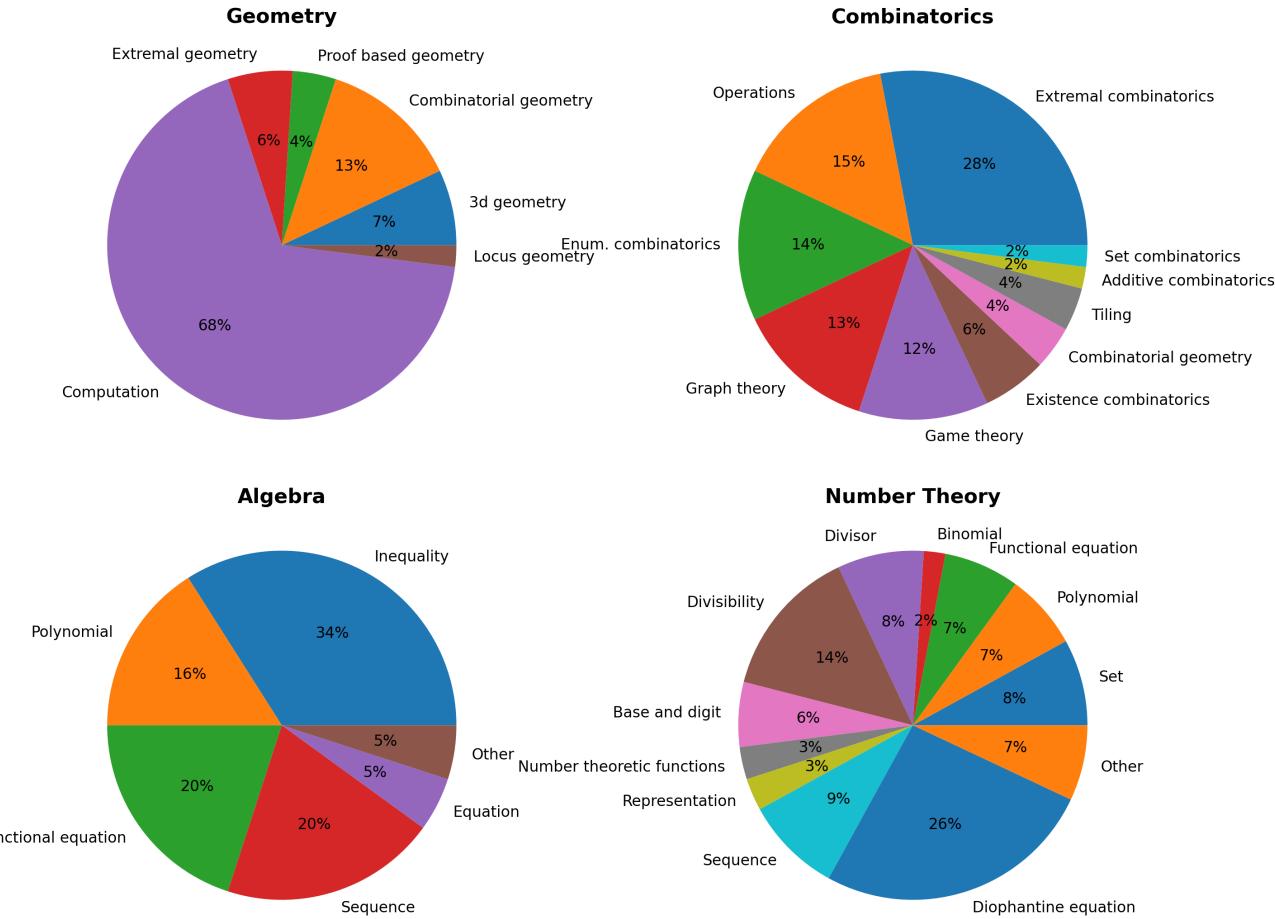
Figure 2 | Topic distributions by domain. Number Theory and Combinatorics encompass the widest range of subtopics, challenging models to reason abstractly.

Making the Benchmark “Robust”

Public benchmarks face a notorious problem: data contamination. If a model has encountered the same question or solution during training, its performance no longer reflects new reasoning.

To overcome this, the authors developed a multi-step process called problem robustification, altering existing Olympiad problems through:

• Paraphrasing language and structure.
• Changing variables (e.g., renaming points in geometry).
• Modifying numerical values to prevent memorization.
• Adding distractors—irrelevant components that increase cognitive load.
• Reformulating equations while preserving core logic.

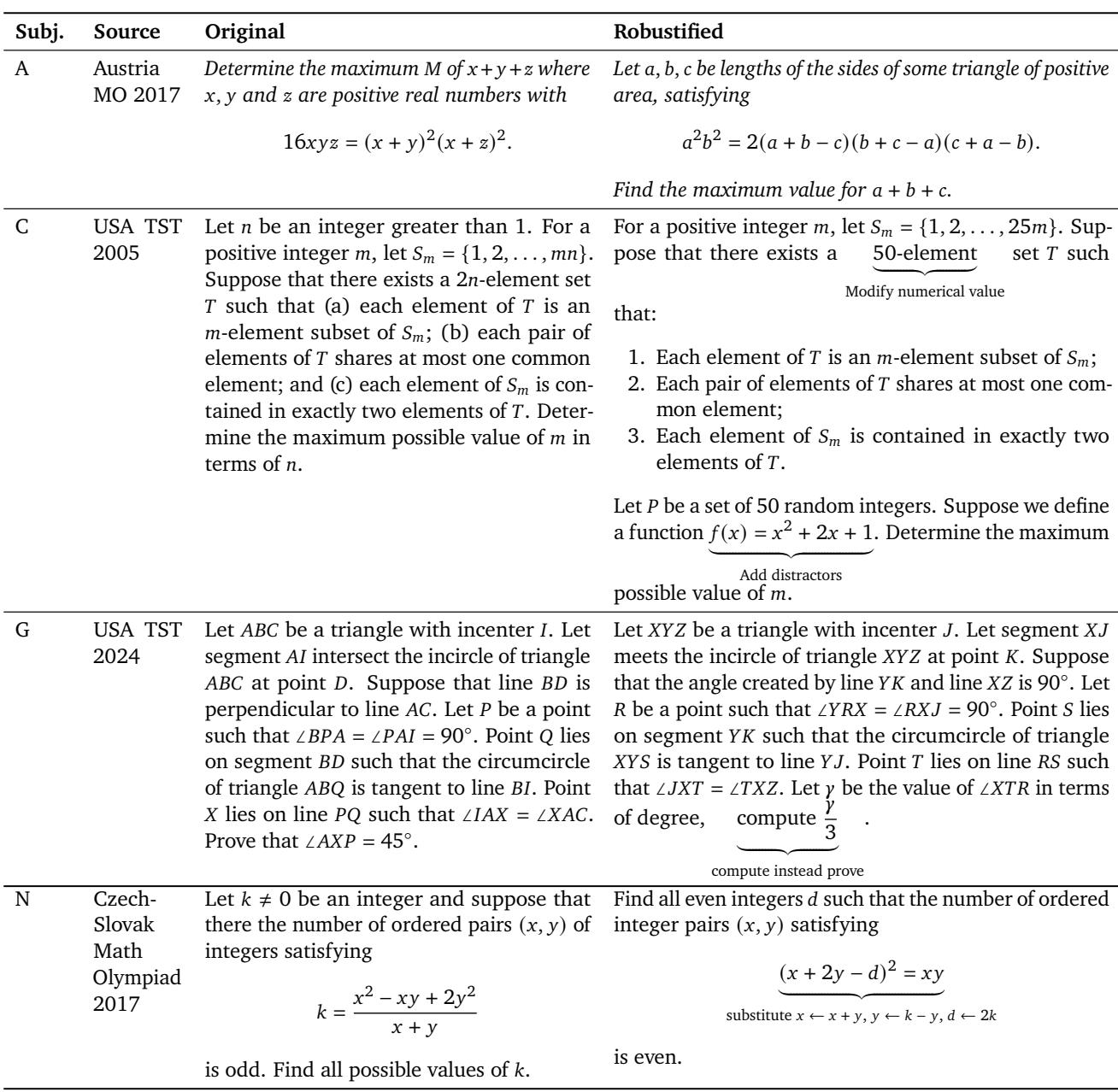
Table 8 | Examples of how Olympiad problems are reformulated to prevent memorization and enforce reasoning from first principles.

Automating the Grading: The AnswerAutoGrader

Even short answers can be tricky to evaluate automatically. For instance, a human knows that “all real numbers except -4” is identical to \((-∞, -4) ∪ (-4, ∞)\), but a script might mark them different.

To solve this, the paper introduced the AnswerAutoGrader, powered by Gemini 2.5 Pro. This model is prompted to extract and verify answers semantically, comparing the mathematical equivalence rather than mere text matching. As shown later, its results track almost perfectly with human grading, allowing large-scale evaluation without sacrificing accuracy.

Part 2: IMO-ProofBench — The Real Test of Reasoning

Getting a correct number is one thing. But can an AI prove why that number is correct?

IMO-ProofBench pushes into this territory. Every problem demands a complete, logically valid proof written in natural language. A final answer without correct reasoning earns no credit.

The benchmark comprises 60 proof-based tasks, divided into two tiers:

1. Basic Set (30 problems): Pre-IMO to medium difficulty, designed for foundational evaluation.
2. Advanced Set (30 problems): Full Olympiad-level challenges, including five complete IMO-style sets and 18 brand-new problems crafted by medalists to ensure novelty.

How Are Proofs Graded?

Evaluating informal proofs is subjective. To standardize this, the researchers adopted the IMO’s official 7-point scale and simplified it into four categories.

Table 3 | Simplified 4-tier rubric used for grading IMO-ProofBench solutions.

While human experts remain the gold standard, manual grading is time-intensive. The team built ProofAutoGrader, another LLM-based evaluator that grades proofs automatically. It receives the problem, the model’s proof, a reference solution, and tailored grading guidelines, providing a detailed assessment.

Though not perfect, ProofAutoGrader shows remarkable promise—achieving near-human level correlation scores, as we’ll see next.

Part 3: IMO-GradingBench — Can Models Judge Other Models?

The final step flips the task: instead of solving, the model must evaluate other solutions.

IMO-GradingBench contains 1000 proof submissions from various models, each graded by expert mathematicians. The model is shown the problem and a proposed solution, then asked to assign one of four grades—Correct, Almost, Partial, or Incorrect.

This benchmark measures a model’s understanding of mathematical reasoning itself. Can it recognize valid logic? Can it detect subtle but fatal errors?

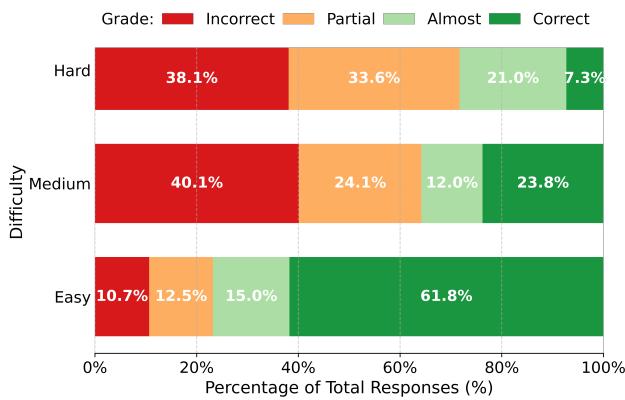
Figure 3 | Human grade distribution in IMO-GradingBench. Harder problems predictably yield higher proportions of incorrect and partial responses.

The Results: How Today’s Models Stack Up

The researchers tested numerous public and proprietary models, and the results reveal where true progress stands.

IMO-AnswerBench — A Clear Leader Emerges

Gemini Deep Think (IMO Gold) leads with a remarkable 80.0% accuracy, outperforming all other models on the short-answer benchmark.

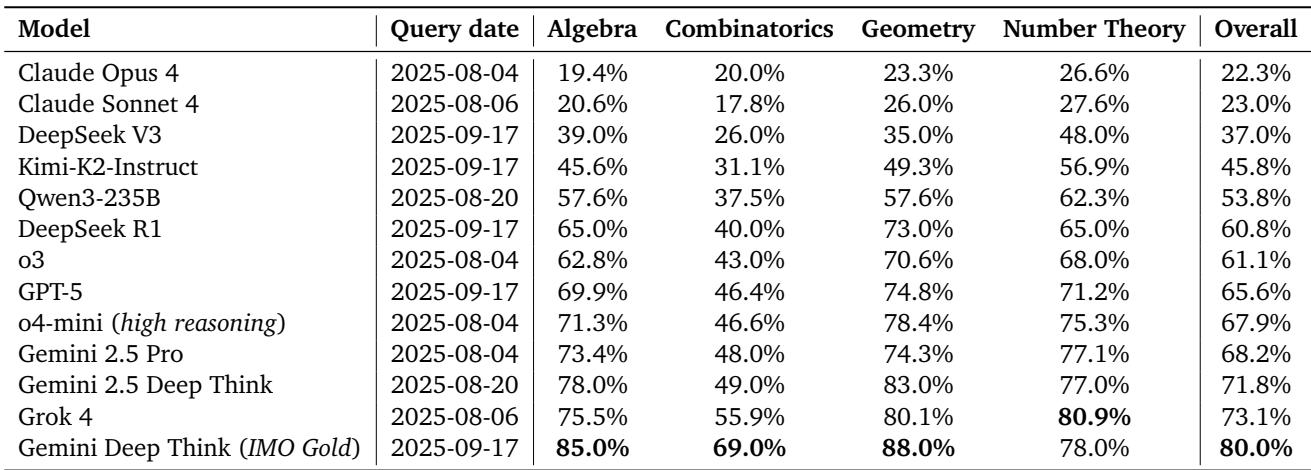
Table 4 | Accuracy performance on IMO-AnswerBench. Gemini Deep Think consistently outperforms across domains.

Key insights:

• Gemini Deep Think surpasses competitors by 6.9% over Grok 4 (best non-Gemini) and by 19.2% over DeepSeek R1 (best open-weight).
• Combinatorics remains the weakest area for most models, highlighting persistent difficulty in abstract combinatorial logic.
• The AnswerAutoGrader achieves near-perfect human agreement (98.9%), validating fully automated grading.

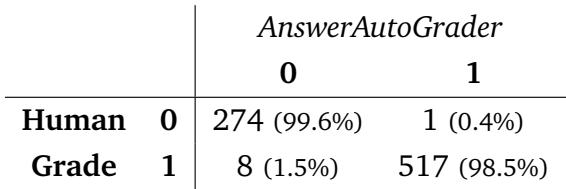
Table 5 | Near-total agreement between automated and human grading for short answers.

IMO-ProofBench — The Great Divide

When moving from answers to proofs, performance gaps become dramatic.

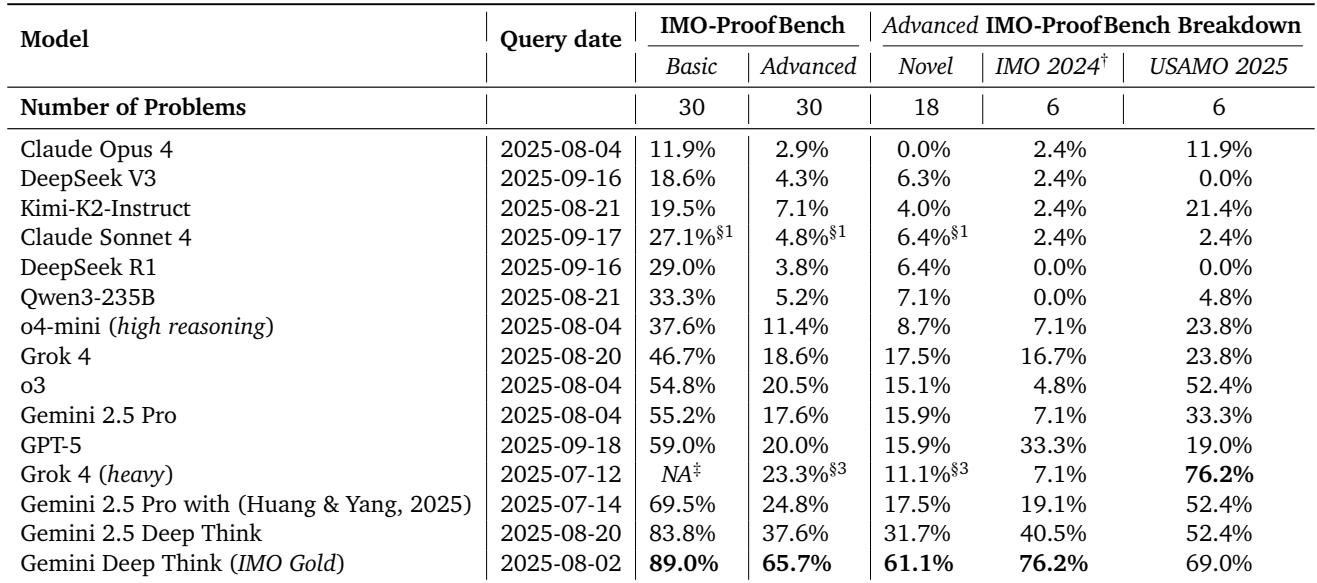
Table 6 | Expert evaluations on IMO-ProofBench. Most models fail to deliver rigorous proofs at Olympiad difficulty.

Observations:

• On the basic set, only a few models exceed 50%. The Gemini Deep Think (IMO Gold) model achieves 89.0%.
• On the advanced set, non-Gemini models collapse below 25%, while the IMO Gold model achieves 65.7%, an astonishing 42.4% lead.
• Breakdown by problem type shows potential overfitting: Grok 4 performs well on familiar USAMO 2025 problems but poorly on novel ones. Gemini Deep Think maintains consistency, indicating genuine generalization.

How Well Does ProofAutoGrader Work?

To measure automated proof grading, the authors compared ProofAutoGrader’s outputs to expert human scores.

On public model evaluations:

• Pearson correlation coefficients: 0.96 (basic), 0.93 (advanced).
• On 170 internal models: r = 0.87, maintaining strong alignment even across varied reasoning quality.

Figure 4 | Consistent alignment between ProofAutoGrader and human evaluation across internal models.

Most disagreements occur between adjacent grading categories (Incorrect vs. Partial).

Figure 5 | Common misclassifications in ProofAutoGrader. Even near-human performance shows the hardest distinctions between close grades.

Overall, ProofAutoGrader demonstrates that scalable proof assessment is feasible. For critical evaluations, human oversight remains recommended, but the groundwork for automated reasoning assessment is solidly in place.

IMO-GradingBench — A Frontier of Meta-Reasoning

This benchmark pushes models to grade others’ proofs without reference solutions, demanding high comprehension skill.

Table 7 | Performance of models on IMO-GradingBench. Accuracy (%) higher is better; Mean Absolute Error (MAE) lower is better.

Key observations:

• The best accuracy (o3) is 54.0%, yet overall results indicate the challenge is immense.
• Gemini Deep Think (IMO Gold) achieves the lowest MAE (18.4%), showing better fine-grained judgment.
• IMO-GradingBench proves that evaluating mathematical reasoning is a frontier challenge—understanding proofs is harder than writing them.

Conclusion: Raising the Bar for AI Reasoning

IMO-Bench sets a new gold standard for evaluating AI in mathematics. Rather than rewarding final answers, it measures creative reasoning and formal correctness—exactly what distinguishes genuine understanding from guesswork.

Key takeaways:

1. The Reasoning Gap Is Real. Models that excel at answer-getting often fail at proof-writing. IMO-ProofBench exposes this discrepancy vividly.
2. Robustness Matters. By rewording and modifying problems, IMO-Bench attacks memorization directly, ensuring tests measure genuine learning.
3. Scalable Evaluation Is Possible. Through AnswerAutoGrader and ProofAutoGrader, the study shows that reliable automated evaluation can complement human expertise.

With the public release of IMO-Bench, the community gains a rigorous, transparent tool to measure genuine mathematical reasoning. As AI systems strive for general intelligence, the path forward may run through the same terrain that challenges human Olympians: the creative frontiers of mathematics.

The challenge has been set. Now, it’s time for the models to prove themselves.