Unlocking Mathematical Discovery with AI: A Deep Dive into AlphaEvolve

The history of mathematics is a story of ideas — flashes of intuition, painstaking exploration, and rigorous proof. Today, a new class of tools is beginning to augment that story: systems that can search, hypothesize, and even suggest proofs. AlphaEvolve, the subject of the research paper “Mathematical Exploration and Discovery at Scale,” is one such system. It marries the generative aptitude of large language models (LLMs) with evolutionary-style program search and careful, automated verification. The result is an agent that can propose, test, and refine mathematical constructions across dozens of problems — sometimes matching existing best-known solutions, sometimes improving them, and occasionally suggesting general patterns that inspire human proofs.

This article walks through what AlphaEvolve is, why it works, and some of the most compelling mathematical outcomes it produced. I focus on intuition, reproducible methodology, and concrete examples so a mathematically-minded reader — whether student, researcher, or practitioner — can understand how these systems are built and how they might be used or improved.

Table of contents

• What AlphaEvolve tries to do (and what it does not)
• The core ideas: evolving code, search heuristics, and generalizers
• The evolutionary loop and the “search mode”
• From experiments to theorems: pipelines with proof assistants
• Practical trade-offs: compute, model choice, and verifiers
• Selected mathematical highlights
• Finite-field Kakeya and Nikodym constructions
• Autocorrelation inequalities (weird extremizers)
• Kakeya needle and packing-style constructions
• Packing problems and human–AI collaboration
• A few more quick wins and near-misses
• Limitations, pathologies, and best practices
• A short roadmap: where this line of work is headed

What AlphaEvolve tries to do (and what it does not) AlphaEvolve is an exploration-and-construction tool. It is designed for problems where the aim is to produce explicit mathematical objects with strong extremal properties: graphs with many edges but forbidden substructures, point configurations minimizing or maximizing energies, discrete sets with small or large sumsets, packings, and so on. It is not a general theorem prover (though it can be part of a pipeline that includes proof systems), and it is not a black box that magically finds deep conceptual breakthroughs in theory. Instead, its power is in large-scale, semi-automated, creative numerical and programmatic exploration: evolving programs that generate constructions, or evolving search heuristics that find constructions quickly.

Why program space? A central insight is that many elegant constructions admit short programmatic descriptions. Searching in the space of short programs — instead of the raw space of candidate objects — tends to favor structured, interpretable, and robust solutions, and it avoids bogging down in combinatorial messes that have no simple description.

A quick illustration: instead of searching over all 50-vertex graphs, each represented by 1225 bits, search over short Python programs that generate graphs. A single LLM mutation might produce a family of closely-related programs that all generate the same (or very similar) high-quality graph. This is often a far better prior for elegant solutions than treating each graph as an independent datapoint.

The core ideas: evolving code, search heuristics, and generalizers AlphaEvolve builds on two complementary techniques:

1. Program evolution with LLMs. The evolutionary “mutations” are generated by an LLM that produces syntactically valid, semantically plausible code modifications. These are far smarter than random edits: the LLM uses its code and math knowledge to propose meaningful changes.

2. Search-mode heuristics. When the verifier (the evaluator) is cheap relative to an LLM call, AlphaEvolve evolves programs that themselves run internal searches. In other words, it evolves search heuristics: programs that, given a time budget, run fast local searches, random restarts, greedy moves, or gradient-based procedures to find good objects. The cost of one LLM call is amortized by the many cheap evaluations that the evolved heuristic performs.

There is also a “generalizer mode”: instead of producing a construction for a single input size (e.g., n = 11), AlphaEvolve is asked to produce a program that performs well across many input sizes. The hope is that, by observing examples for many small n, the system will spot patterns and produce a compact, general algorithm (or even a formula).

The evolutionary loop and the “search mode” At a high-level the system proceeds in generations:

• Maintain a population of programs (candidates).
• Select above-average programs to seed LLM mutations.
• Use an LLM to produce mutated offspring programs (intelligent edits).
• Run a verifier (fitness function) on each offspring. For search-mode runs, the offspring program itself will run many cheap evaluations (it is a search heuristic given a time budget).
• Keep the best programs and repeat.

Why the “search mode” matters LLM queries are relatively expensive. If the verifier can evaluate millions of raw candidates in the time it takes the LLM to mutate code once, it is wasteful to evolve programs that only themselves output a single candidate. In search mode, each evolved program runs a time-bounded search to generate many candidates cheaply. We score the heuristic by the best candidate it discovers. This unlocks a multiplier effect: one expensive LLM call → many cheap numerical trials.

This mode also enables dynamic specialization: early heuristics focus on exploration, later heuristics on refinement. The evolutionary process often produces a chain of specialized heuristics that, when composed, yield excellent constructions.

The “generalizer mode”: going from examples to formulas Search mode is for optimizing a single instance; generalizer mode is for recognizing patterns. In practice, AlphaEvolve is evaluated on many n values during evolution, with the score being an aggregate (e.g., average normalized quality). This encourages programs that generalize. Successes here have been among the most interesting outcomes: AlphaEvolve sometimes proposes compact algorithms or parameterized constructions that work across many inputs, and human researchers (and other AI tools) have been able to formalize or generalize these ideas further.

The AI pipeline: discovery, proof, and verification A particularly appealing workflow is the pipeline:

• Pattern discovery (AlphaEvolve): propose a programic construction that empirically performs well for many inputs.
• Symbolic reasoning (Deep Think): attempt to derive proofs or closed-form expressions for the observed sizes or properties.
• Formal verification (AlphaProof + Lean/mathlib): convert the symbolic proof into a fully formalized Lean proof, where possible.

This pipeline was demonstrated on finite-field Kakeya/Nikodym experiments: AlphaEvolve suggested programmatic constructions, Deep Think derived closed-form formulas and proofs, and AlphaProof helped formalize parts of the derivation in Lean. The synergy is important: AlphaEvolve is strong at proposing candidates; other systems are stronger at symbolic or formal reasoning. Combined, they allow a path from numerical discovery to formal theorem.

Practical trade-offs: compute, model choice, and verifiers The paper presents careful ablations and meta-analyses. Here are the most actionable lessons.

Compute vs. time-to-solution More parallel CPU threads (or more GPU resources) lead to faster discoveries but increase total LLM calls and thus cost. In experiments on an autocorrelation inequality (Problem 6.2), runs with 20 CPUs reached better-than-state-of-the-art bounds much faster than runs with 2 CPUs, but used more LLM calls overall.

Model choice: big vs. cheap LLMs Stronger LLMs generate higher-quality program mutations and tend to reach good solutions with fewer mutation steps. That said, cheaper LLMs add exploratory diversity; in some problems the cheapest model run many times (cheap diversity) proved cost-effective for achieving state-of-the-art numerical bounds. For harder, more structured problems, top LLMs are more valuable.

Designing verifiers carefully The verifier (fitness function) is critical. Poorly designed verifiers can be “cheated”: the evolved program can exploit numerical artifacts, approximations, or loopholes. Two recommendations:

• Prefer continuous, informative losses (when sensible) over brittle discrete penalties. Continuous losses supply steady gradients for heuristics and avoid plateaus where the search stalls.
• Validate candidate solutions with stricter, higher-precision verifiers post-discovery. Use rational arithmetic or interval arithmetic to certify numerical near-equalities.

Selected mathematical highlights AlphaEvolve was tried on 67 problems across combinatorics, geometry, analysis, and number theory. I cannot cover all of them in depth here, but below I select representative examples that illustrate different facets of the approach.

A head-to-head overview (visual summary)

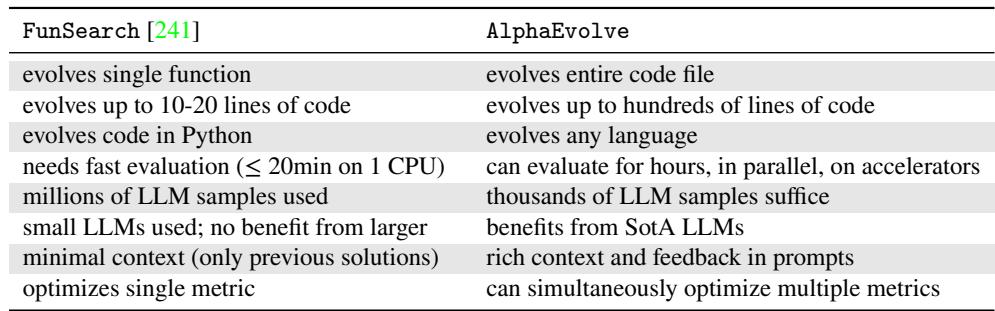
Comparison: FunSearch vs. AlphaEvolve — program scope, evaluation scale, and dependence on LLMs.

1. Finite-field Kakeya and Nikodym constructions (generalizer mode) Problem sketch. In \(\mathbf{F}_q^d\), a Kakeya set contains a line in every direction; a Nikodym set is a set \(N\) such that every point \(x\) is contained in a line that is contained in \(N \cup \{x\}\). Asymptotically the minimal Kakeya set sizes behave like \(\approx q^d/2^{d-1}\); refining lower-order terms is delicate and often number-theoretic.

What AlphaEvolve did. Using generalizer mode, AlphaEvolve proposed programmatic constructions evaluated on many primes \(p\). For \(d=3\) it rediscovered and slightly refined known constructions: for primes \(p \equiv 1 \pmod 4\) it produced a Kakeya set of size

matching the leading terms from literature and slightly improving lower-order coefficients. The system produced candidates that Deep Think could analyze symbolically; in one case Deep Think produced a closed-form formula whose correctness was then formalized in Lean by AlphaProof.

Why this is notable. The constructions required number-theoretic structure (quadratic residues, polynomial constraints), and AlphaEvolve found the right structural form without being explicitly given the key references. This shows the system can discover or reconstruct constructions with deep arithmetic content.

2. Autocorrelation inequalities: highly irregular extremizers Autocorrelation problems ask how closely the convolution \(f * f\) can approximate certain shapes or bound certain norms. These optimizers can be wildly irregular or fractal-like.

Problems 6.2 and 6.3. AlphaEvolve searched over piecewise-constant functions (fixed partition), evolving heuristics that perturb coefficients and combine gradient steps with heuristic backtracking. The system reduced the best-known upper bound in Problem 6.2 to \(1.5032\) and produced a suite of high-quality counterexample functions. For Problem 6.3 (a different convolution inequality) AlphaEvolve, after discovering that gradient methods work, combined them with evolved heuristics to produce a step function with 50,000 parts that pushed the lower bound to \(0.961\). The extremizers were very irregular — suggestive of why human intuition or simple gradient runs alone struggle in this landscape.

Representative figure: example extremizers and autoconvolutions

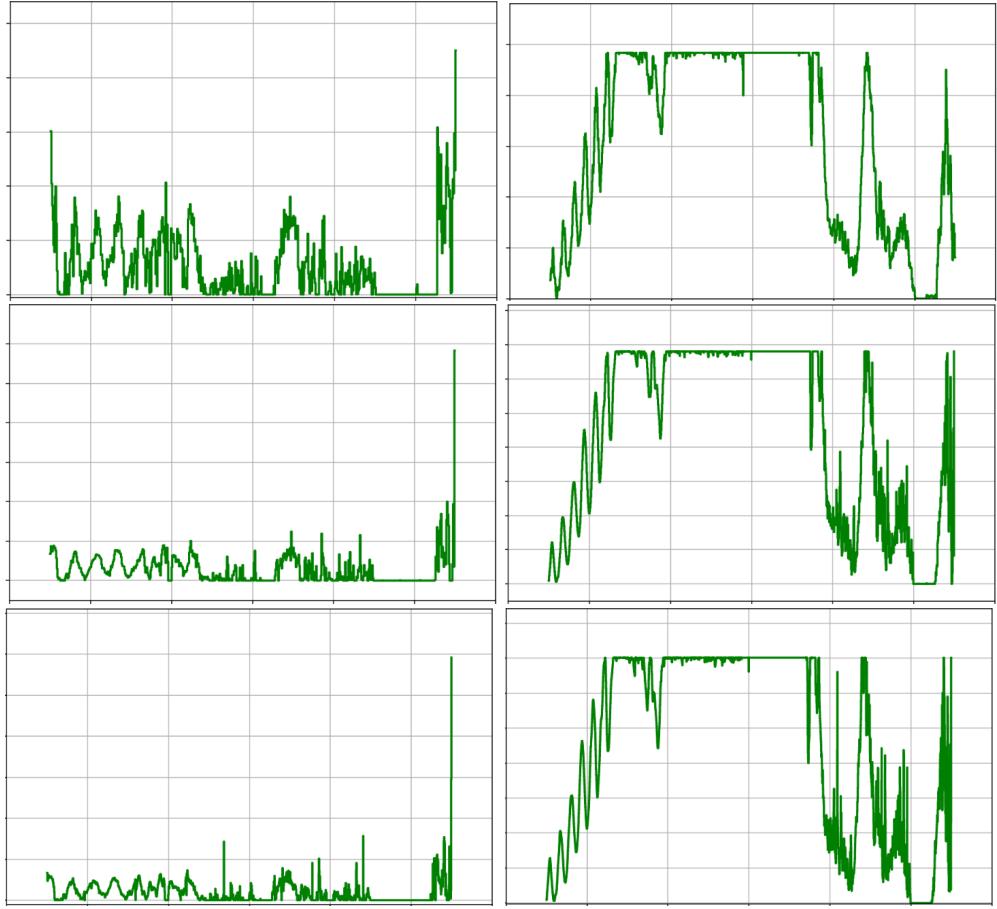
Constructed step functions and their autoconvolutions for Problem 6.2. These functions are highly irregular and difficult to describe analytically.

A best single function for Problem 6.3 (50,000-step approximation)

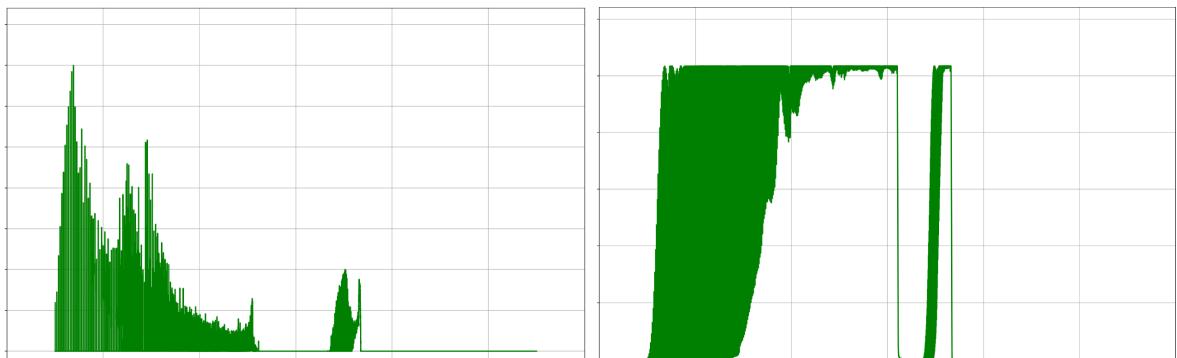
A 50,000-step piecewise-constant function discovered by AlphaEvolve that improved a lower bound for an autoconvolution inequality (Problem 6.3).

3. Kakeya needle problem (geometric optimization) Problem sketch. The Kakeya needle problem (Besicovitch) asks how small an area one needs to rotate a unit-length segment through 360 degrees. Discrete formulations ask, for a fixed number \(n\), how to place \(n\) triangles or parallelograms to minimize union area or maximize related scores.

What AlphaEvolve did. In search mode it evolved heuristics that produced triangle and parallelogram placements. For many n it produced layouts with smaller union area than the constructions of Keich, and when asked to produce generalizable programs it found compact algorithms capturing Keich-like bitwise constructions and their generalizations to non-power-of-2 values of \(n\). The evolved constructions often looked irregular and non-self-similar compared to classical schemes, yet numerically outperformed them for the tested ranges.

Performance vs. classical scheme

Left: total area vs. n for triangles/parallelograms. Right: related performance scores (AlphaEvolve vs. Keich).

Visual comparison: Keich vs. AlphaEvolve patterns

Keich constructions (top) versus AlphaEvolve’s evolved constructions (bottom) for various \(n\).

4. Packing problems and collaboration AlphaEvolve tackled many packing problems — circles in squares, hexagons packing into a larger hexagon, unit cubes inside larger cubes, and more. These problems are practical, visual, and well-suited to search-mode heuristics that combine random starts with local relaxations.

Notable wins and human-AI collaboration:

• Hexagon packings: AlphaEvolve improved the best-known arrangements for \(n=11\) and \(n=12\) unit hexagons inside a larger hexagon. These constructions were later analyzed and slightly refined by a human expert (symmetry adjustments), illustrating a powerful workflow: let AlphaEvolve explore freely, then apply human geometry insight to obtain the final optimum.
• Cube packings: AlphaEvolve improved the upper bound for packing 11 unit cubes into a larger cube (side length \(\approx 2.895\)), producing a new record arrangement.

Examples: hexagon and cube packings

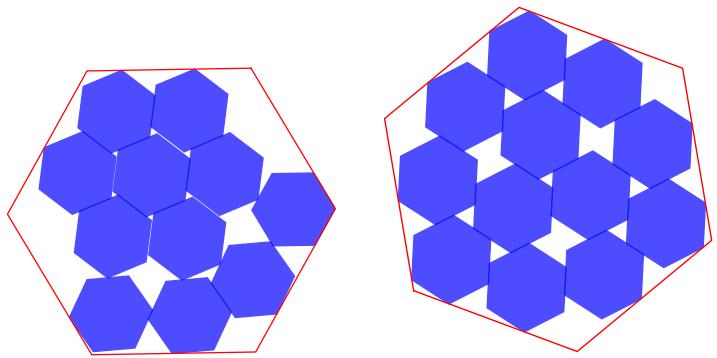
Improved hexagon packings (11 and 12 unit hexagons) found by AlphaEvolve.

A cube-packing improvement for \(n=11\) unit cubes.

5. Block stacking and generalization (an illustrative, didactic success) The block-stacking (overhang) problem has a classical solution: the maximal overhang for \(n\) identical unit-length blocks is \(\tfrac{1}{2}H_n\), where \(H_n\) is the \(n\)-th harmonic number. AlphaEvolve used generalizer mode in this setting: it found optimal finite-\(n\) stacks, guessed the recurrence, and then produced the harmonic-formula-based construction as a general program. This is a clean example of the system moving from small-instance data to a general construction.

A depiction of the canonical stacked solution (intuition)

A 5-block stack achieving the harmonic overhang. AlphaEvolve rediscovered the general pattern programmatically.

6. An IMO construction discovered programmatically AlphaEvolve was used to write a program that constructs optimal tilings for an IMO 2025 Problem (tiling an \(n\times n\) square so each row and column has exactly one uncovered cell). When evaluated on perfect-square \(n\) it produced the optimal number of tiles and often the optimal tilings themselves. This is an encouraging demonstration that AlphaEvolve can succeed on constructive contest-style problems, producing code that yields the desired combinatorial objects.

An optimal tiling (visual)

A compact optimal tiling produced by an evolved program for a contest-style constructive problem.

A few more quick wins (and near-misses)

• Kissing numbers: AlphaEvolve improved the lower bound for the kissing number in 11 dimensions from 592 to 593.
• Tammes and Thomson problems (point energies on spheres): AlphaEvolve matched many known optimal configurations and produced high-precision numerical candidates for larger \(N\).
• Combinatorial set constructions: It improved lower bounds on some sum-difference and packing-related constants by discovering large explicit sets with desirable properties.
• Harder targets where it fell short: some problems requiring deep analytic structure or entirely new theoretical techniques were not improved (and some remain “AlphaEvolve-hard”).

Limitations, pathologies, and best practices AlphaEvolve is powerful, but it is not magic. The paper — and the experiments summarized above — highlight important caveats.

1. Verifier design is crucial. If the verifier is sloppy or uses low precision, the evolved programs will exploit loopholes. Example failures included programs that used numerical quirks to appear to achieve impossible scores. Always verify promising candidates with a stricter verifier using higher precision or exact arithmetic.

2. Data contamination and prompt design. Because AlphaEvolve uses LLMs, care must be taken to avoid leaking solutions in prompts or to avoid overly prescriptive hints that bias the search unhelpfully. At the same time, a small amount of expert guidance often greatly improves performance. The right balance depends on whether the goal is pure discovery (less hinting) or targeted improvement (more domain knowledge).

3. The randomness–diversity trade-off. Strong LLMs give high-quality edits, but cheaper or more naive models introduce diversity that can help escape local optima. Mixtures of models can be effective.

4. Interpretability can vary. Evolving search heuristics can produce black-box strategies that are hard for humans to analyze. When interpretability matters, favor evolving concise program templates or use generalizer mode to encourage compact algorithms.

5. Computational reproducibility. Because the evolutionary process can be stochastic, reproducing exact mutations can be costly. The paper and repository provide seeds, prompts, and verifiers to reproduce most results with enough compute, but expect variability across runs.

Concluding thoughts and a short roadmap AlphaEvolve shows that LLMs combined with evolutionary program search and rigorous evaluators can accelerate mathematical exploration at scale. Key strengths:

• It converts expensive LLM creativity into many cheap numerical evaluations via search-mode heuristics.
• It discovers both ad-hoc constructions and sometimes general programs that generalize across input sizes.
• It plugs into a broader pipeline with symbolic reasoners and proof assistants to move from pattern to proof to formal verification.

Important open directions:

• Better auto-verifiers and certification: incorporate interval arithmetic, rational arithmetic, and verified numerics into the pipeline more deeply to avoid “cheating” and to produce machine-checkable certificates for numerical constructions.
• Automated hyper-hyperparameter selection: allow the system to adapt its mutation rates, population sizes, and model mixtures dynamically.
• Deeper integration with proof systems: automate the translation from programmatic construction to proof sketches that symbolic engines can refine.
• Benchmarks and standardized evaluators: construct independent benchmarks for “AlphaEvolve-hard” problems to map out which mathematical activities are amenable to this paradigm.

Final takeaway AlphaEvolve is not a replacement for mathematical insight. It is a new kind of collaborator: a computational explorer that can amplify human intuition, suggest unexpected constructions, and accelerate the search for extremal examples. Combined with human expertise and complementary AI tools (symbolic provers, formalizers), it opens new workflows for discovery — turning vast, previously intractable search spaces into structured opportunities for creativity.

If you want to experiment with AlphaEvolve-style methods, a practical checklist to start:

• Define a crisp verifier: make the score precise, continuous if possible, and able to be tightened for final validation.
• Start in search mode: evolve heuristics rather than single constructions when the verifier is cheap.
• Run mixed-model strategies: strong LLMs polished with cheap-model diversity can pay off.
• Validate with exact/rational checks before claiming improvements.
• Consider generalizer mode if you want patterns or formulas, and constrain the training inputs to encourage abstraction.

The repository that accompanies the paper contains code, prompts, verifiers, and many of the programmatic constructions mentioned here. For practitioners, the message is straightforward: with the right verifier and the right prompts, LLM-guided program evolution can become a highly practical tool for mathematical exploration and construction.

Acknowledgement: the research described in the paper was an extensive team effort combining applied ML engineering, mathematical expertise, and significant compute. The ideas and results summarized here represent a snapshot of an active research frontier that blends generative models, optimization, and formal mathematics.

Further reading

• The full research paper: “Mathematical Exploration and Discovery at Scale” (authors: B. Georgiev, J. Gómez‑Serrano, T. Tao, A. Z. Wagner).
• The accompanying repository of problems and code (linked from the paper).
• Related systems: AlphaProof, Deep Think, and earlier systems such as FunSearch and PatternBoost.

Thanks for reading. If you work on constructive or computational mathematics, consider how a tool like AlphaEvolve could augment your workflow: it is especially good at generating candidate constructions and heuristics that a human can then analyze, simplify, or formalize.