Masked diffusion models have emerged as one of the most powerful frameworks for generative modeling. From complex reasoning and language generation to image synthesis and molecular design, these models can iteratively refine masked data to produce coherent, high-quality outputs.

Yet, despite their promise, masked diffusion models suffer from a notorious bottleneck: slow inference. Their iterative decoding process—where only one or a few tokens are unmasked per step—leads to hundreds of sequential sampling rounds. This dramatically limits their use in real-world applications that demand quick, responsive generation.

The research paper “KLASS: KL-Guided Fast Inference in Masked Diffusion Models” from KAIST introduces a simple but elegant solution: KL-Adaptive Stability Sampling (KLASS). Instead of using fixed unmasking rules, KLASS allows the model to decide how many tokens to reveal at each step based on its internal confidence and stability signals. The result? Faster sampling, better accuracy, and no extra training required.

In this deep dive, we’ll unpack how KLASS works, why stability matters, and how it redefines efficiency in diffusion-based generation across text, reasoning, images, and molecular tasks.

A Quick Refresher: What Are Masked Diffusion Models?

Imagine you have a clean, complete sentence. The diffusion model’s forward process gradually corrupts it by replacing words with a special [MASK] token until the entire sentence becomes masked. The model then learns the reverse process: restoring the original data step by step.

Formally, the forward process at timestep \(t\) can be described as an absorbing process that replaces tokens with mask indices \(\mathbf{m}\), controlled by a noise schedule \(\alpha_t\) that decreases over time.

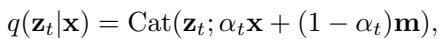
Equation for the forward process in masked diffusion models.

Figure: The forward process progressively replaces clean tokens with masks under a noise schedule \(\alpha_t\). The reverse model learns to predict the original tokens from these masked sequences.

During inference, we start from a fully masked sequence and iteratively apply the learned reverse process, sampling:

\[ x_{t_{i-1}} \sim p_\theta(x_{t_{i-1}} \mid x_{t_i}) \]

at each step of the Ancestral Sampling process.

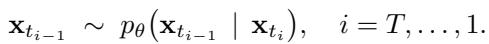
Equation for ancestral sampling in masked diffusion models.

Figure: Ancestral Sampling reverses the masked diffusion, refining predictions at each step until all tokens are unmasked.

Standard samplers such as Top-1 or Top-k are static—they reveal a fixed number of tokens per step. Even if the model is highly confident about many tokens simultaneously, these samplers unmask just a few, resulting in excessive sequential computations.

KLASS changes this paradigm by allowing dynamic, model-driven unmasking based on token-level behavior.

The Core Method: KL-Adaptive Stability Sampling (KLASS)

Traditional methods use prediction confidence to decide which tokens to unmask. But high confidence doesn’t always mean correctness—a confident model can still pick the wrong token. KLASS introduces a second, more reliable signal: stability, captured by the Kullback-Leibler (KL) divergence between consecutive predictions.

Together, confidence and stability form a robust way to decide when to trust the model.

Two Signals Are Better Than One: Confidence and KL Score

KLASS defines two simple but complementary metrics for every token position \(i\) at timestep \(t\):

1. Confidence Score

\[ \operatorname{conf}_{t}^{i} = \max_{v \in V} p_t^i(v) \]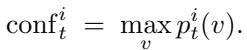

Equation for the confidence score.

Figure: Confidence score measures how strongly the model prefers its top prediction for each token.

A high confidence score means the model is certain. However, confidence alone can be misleading—it may latch onto a wrong token early.

2. KL Score (Stability Score)

\[ d_t^{i} = D_{\mathrm{KL}}(p_t^{i} \parallel p_{t+1}^{i}) \]

Equation for the KL score.

Figure: The KL score tracks how much the model’s probability distribution for a token changes between steps. Lower values signal stable predictions.

A low KL score means the distribution has barely changed—the model’s belief has stabilized. High KL indicates that the model is still uncertain or changing its mind.

The authors found that correct predictions consistently have lower KL divergence than incorrect ones, as shown below.

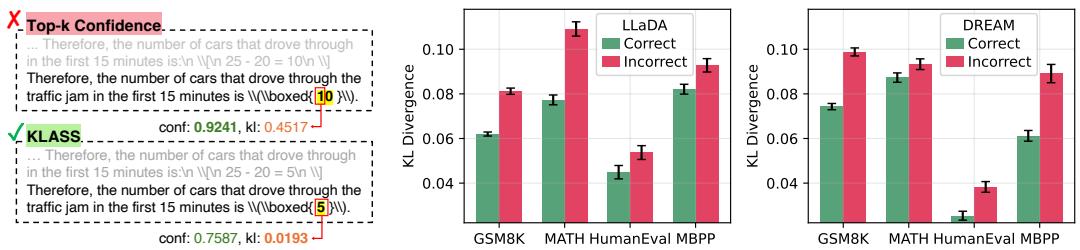
KL divergence as a strong indicator of solution correctness. Part (a) shows KLASS choosing a correct, low-KL token over a high-confidence but incorrect one. Part (b) shows that across benchmarks, correct predictions have lower average KL divergence.

Figure 1: KL divergence as a strong indicator of correctness. Correct tokens show much lower KL values than wrong ones, making stability a better predictor of reliability than raw confidence.

The KLASS Algorithm in Action

KLASS combines these two metrics into a dynamic decoding routine. At every timestep \(t\), the model examines all masked tokens and decides which ones are sufficiently stable to unmask.

A token is deemed stable if:

  • Its confidence exceeds a threshold \(\tau\), and
  • Its KL divergence has remained below a small threshold \(\epsilon_{\mathrm{KL}}\) for the past \(n\) steps.

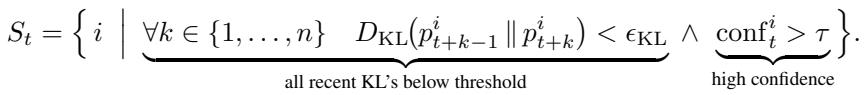
Equation for selecting the set of stable tokens in KLASS.

Equation: Stable token selection checks both high confidence and low-KL consistency over a short history window.

KLASS then unmasks all tokens in this stable set \(S_t\) in parallel:

The KLASS unmasking rule. It unmasks all stable tokens, or falls back to a Top-u strategy if no stable tokens are found.

Figure: KLASS unmasking logic. If no tokens meet stability criteria, it falls back to unmasking the Top-u most confident tokens to ensure steady progress.

This adaptive process allows the model to dynamically speed up or slow down based on its certainty—revealing large portions when predictions are consistent, and hesitating when uncertainty remains high.

Figure 2 captures this beautifully. Tokens are only revealed once both criteria (confidence and stability) are satisfied.

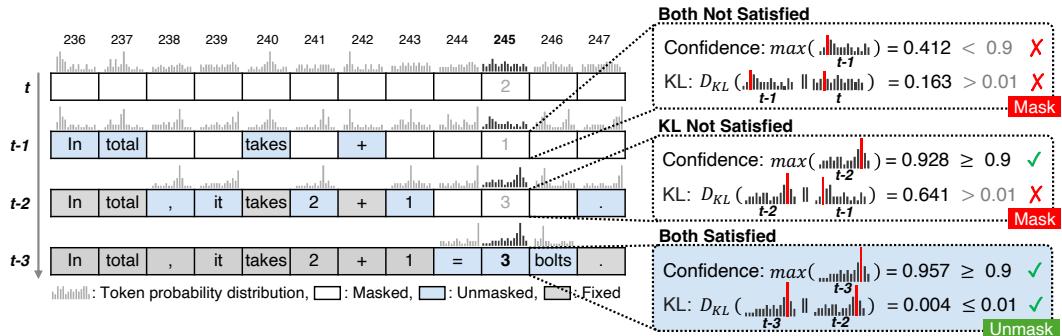
Illustration of parallel decoding with KLASS. Tokens are unmasked only when both high confidence and low KL-divergence criteria are met.

Figure 2: KLASS parallel decoding. The model unmaskes multiple tokens at once when both stability and confidence thresholds are satisfied, enabling substantial acceleration without harming accuracy.

Theoretical Insight: The paper also proves that incorrect tokens are inherently unstable. As surrounding context becomes correct, their conditional distributions must shift, resulting in higher KL divergence. This means waiting for stability is not just practical—it’s mathematically grounded.

Experiments: Putting KLASS to the Test

KLASS was evaluated across reasoning, text, image, and molecular generation tasks using large-scale masked diffusion models.

High-Stakes Reasoning: Math and Code Generation

The authors tested KLASS on reasoning benchmarks like GSM8K, MATH, HumanEval, and MBPP using the LLaDA (8B) and Dream (7B) models.

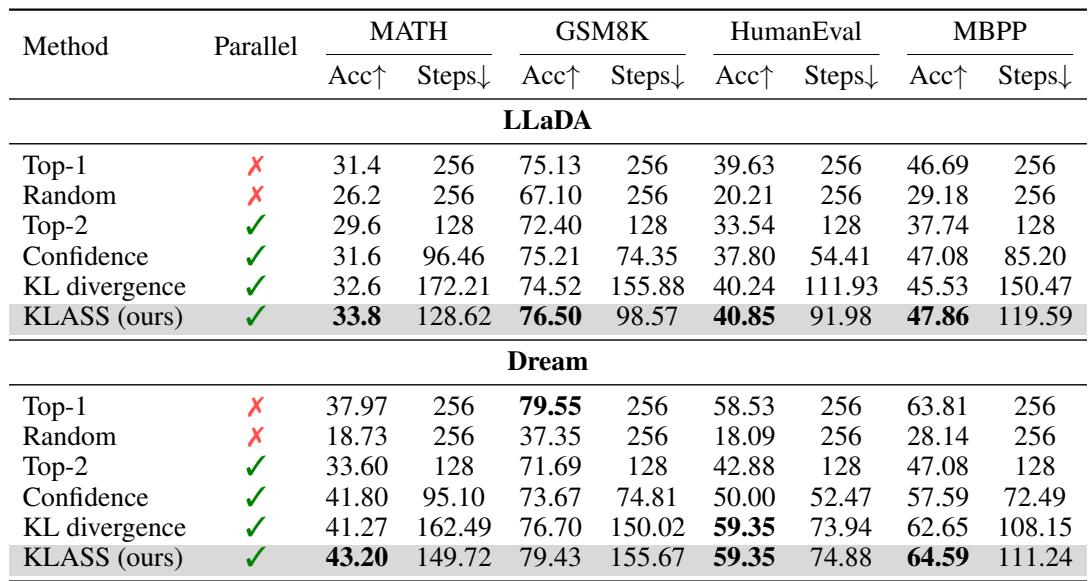
Table 1 shows the performance of KLASS and other samplers on reasoning benchmarks. KLASS achieves higher accuracy with fewer steps.

Figure/Table 1: KLASS improves both speed and accuracy across reasoning tasks, outperforming all existing diffusion samplers.

KLASS achieved up to 2.78× speedups while simultaneously increasing accuracy. For example, on GSM8K (LLaDA), steps dropped from 256 to 98 while accuracy rose from 75.13% to 76.50%. Methods that relied solely on confidence or KL metrics lagged behind—only their combination provided optimal results.

General Text Generation

KLASS next tackled unconditional text generation with the Masked Diffusion Language Model (MDLM), comparing its performance to autoregressive and diffusion baselines.

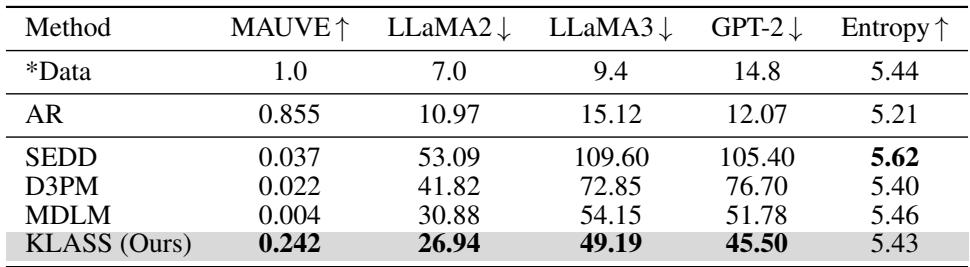
Table 2 shows text generation quality metrics. KLASS achieves higher MAUVE and lower perplexity than other diffusion samplers.

Figure/Table 2: KLASS achieves higher MAUVE scores (distributional closeness to real text) and lower perplexity, producing more coherent and fluent text.

Across multiple oracle language models (LLaMA2, LLaMA3, GPT-2), KLASS significantly reduced perplexity while maintaining strong entropy, resulting in texts that are both diverse and natural.

Beyond Text: Images and Molecules

KLASS demonstrated its generality by being applied to image and molecular generation tasks.

Tables 3 and 4 show that KLASS improves image generation (lower FID, higher IS) and molecular generation (higher reward).

Tables 3–4: KLASS leads to superior image fidelity (lower FID, higher IS) and generates molecules with improved target properties (higher QED and ring count scores).

These results show that KLASS’s adaptive mechanism generalizes seamlessly across modalities—it’s a general-purpose acceleration technique for diffusion inference.

Why Does This Work? Ablation Studies

Ablation experiments confirm that both confidence and KL-divergence thresholds are essential.

Figure 3 shows heatmaps of accuracy for different KL and confidence thresholds. Adding a KL threshold consistently improves performance.

Figure 3: Accuracy improves consistently when a KL threshold is introduced alongside confidence filtering. The two signals enhance each other’s effectiveness.

Another experiment tested parallel vs. single-token unmasking strategies. Parallel unmasking—unmasking multiple stable tokens at once—resulted in dramatically fewer steps and higher accuracy. It effectively gave the model richer context for its remaining predictions.

Finally, the authors examined computational overhead. Despite its sophistication, KLASS is remarkably lightweight: computing token-level KL scores adds only 1.57% memory and 0.21% latency per decoding step.

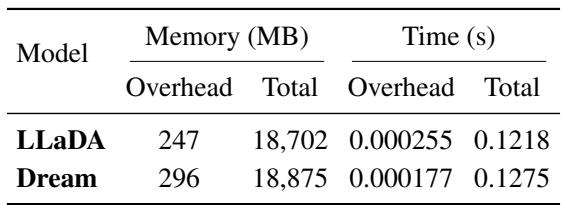
Table 6 shows that the computational and memory overhead of calculating KL divergence is minimal.

Table 6: KL computation overhead is negligible, requiring no additional forward passes or complex operations.

Conclusion: A New KLASS of Sampler

KL-Adaptive Stability Sampling introduces a new way to accelerate diffusion inference—by listening to the model’s own internal dynamics. Instead of relying solely on confidence, KLASS measures stability over time, treating consistency as the stronger signal of correctness.

In summary:

  • Fast & Efficient: KLASS achieves up to 2.78× speedups while cutting sampling steps by more than half.
  • Improved Accuracy: It enhances performance even as decoding gets faster.
  • Training-Free & General: Works out-of-the-box across text, image, and molecular domains without any retraining.

By combining confidence and KL-divergence stability, KLASS shows that generative models can reason about their own certainty—unlocking faster, more reliable predictions and paving the way for smarter diffusion sampling.

This marks not just a faster method, but a smarter one: a new class of sampling grounded in the stability of learning itself.