Large language models (LLMs) like GPT-4 have redefined the limits of artificial intelligence. They can generate code, craft essays, and explain concepts with a human-like fluency. Yet despite their capabilities, their inner workings remain largely mysterious. Inside these models are billions of parameters forming intricate webs of connections — so complex that we often call them “black boxes.” We can observe the inputs and outputs, but not the reasoning in between.

This absence of transparency isn’t just an academic problem; it’s a pressing issue for safety, trust, and alignment. Without understanding why a model chooses a particular output, it’s impossible to predict or verify its behavior in critical situations.

The field of mechanistic interpretability aims to solve this mystery. It seeks to reverse-engineer neural networks, tracing the internal “circuits” that generate specific behaviors. In the OpenAI paper Weight-sparse transformers have interpretable circuits, researchers introduce a striking new approach to this challenge. Instead of dissecting an already dense model, they build one that’s interpretable by design—a transformer trained so that most of its weights are forced to be zero.

By enforcing sparsity, the resulting models become radically simpler, their internal computations disentangled into clear, human-understandable algorithms. What emerges are neural circuits that can be mapped, described, and validated with precision.

The Problem: Superposition

Before exploring the method, we must understand a major obstacle in neural network interpretability: superposition.

Imagine you have a tiny closet (the model’s neurons) and a vast wardrobe (the concepts it needs to represent). To make everything fit, you stuff several outfits into each box. A single neuron might fire for “the color red,” “danger,” and “sentence ending” — all at once. That entanglement of features inside shared neurons is superposition.

In dense models, superposition is ubiquitous. It’s why explanations like “this neuron detects the start of a quote” usually turn out to be partially true — the same neuron might also represent unrelated concepts. Such polysemantic behaviors make the network hopelessly tangled.

The challenge of mechanistic interpretability is to untangle these overlaps. Improving clarity means finding a way for models to represent individual concepts independently.

The Insight: Enforcing Simplicity with Sparsity

The authors propose a radical simplification: allow a model to have a huge capacity, but forbid it from using most of it.

They train weight-sparse transformers where nearly all connections—about 999 out of every 1000—are set to zero. This constraint encourages neurons to specialize. Each neuron can only connect to a few others, ensuring compact and disentangled computation. As a result, circuits inside the model are easier to isolate and interpret.

The workflow behind this approach unfolds in two major stages:

  1. Train a weight-sparse transformer: The model is pretrained from scratch on a Python code dataset, with strict sparsity constraints enforced via an \( L_0 \) norm penalty on weights.

  2. Prune to find interpretable circuits: After training, the researchers identify the minimal subset of nodes—the circuit—necessary to perform a specific task, such as closing a string or predicting the end of a list. Nodes outside the circuit are ablated by setting their activations to a constant mean over the training distribution.

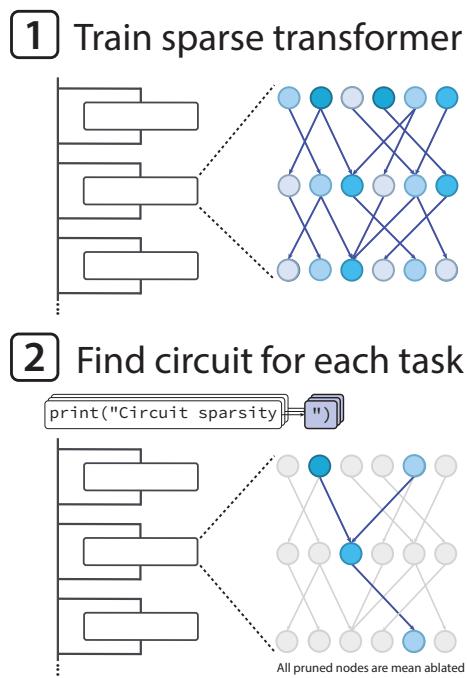
An illustration of the two-step process: first training a sparse transformer, and second pruning it to find the minimal circuit for a specific task.

Figure 1. The research workflow: train sparse transformers, then prune them to isolate interpretable circuits for specific tasks.

This procedure isolates the network components that are both necessary and sufficient for a given behavior. The smaller the resulting circuit, the higher the interpretability.

Results: Simpler Circuits, Sharper Insights

Sparse Models Learn Compact Circuits

To measure interpretability quantitatively, the researchers trained both sparse and dense transformers on 20 small Python coding tasks—each designed to demand discrete reasoning (such as deciding whether to close a bracket with ] or ]]). For each task, they pruned models to achieve equivalent performance and counted the resulting circuit size.

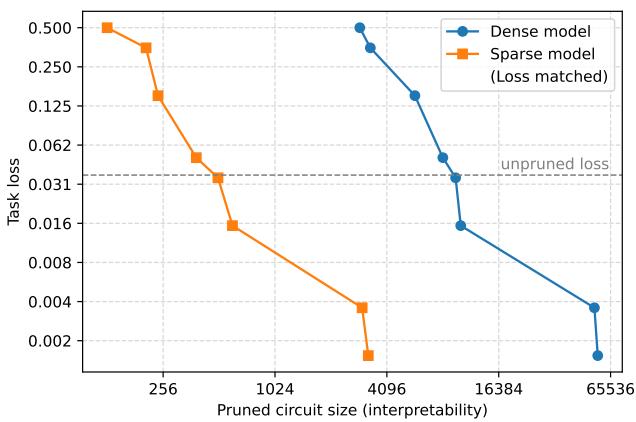
A chart comparing the size of pruned circuits in dense vs. sparse models. The sparse model consistently finds much smaller circuits for the same task loss.

Figure 2. Sparse models yield dramatically smaller circuits—roughly 16× smaller at equal performance—highlighting clearer internal organization.

Sparse models achieved similar accuracy using circuits about 16 times smaller than those of dense models. This demonstrates that weight-sparse training pushes models to distribute information in disentangled, localized computations.

Scaling the Interpretability–Capability Frontier

Naturally, forcing sparsity limits overall capability. However, Figure 3 shows an encouraging trade-off curve. As models grow larger while maintaining a constant number of non-zero parameters, both capability and interpretability improve. In other words, larger sparse models can be more capable and more understandable at once.

A Pareto frontier chart showing the trade-off between pretraining loss (capability) and pruned-circuit size (interpretability). Larger models improve the frontier.

Figure 3. Scaling total parameters under sparsity improves both capability and interpretability—pushing the Pareto frontier down and to the left.

This scaling behavior suggests that interpretability might not have to come at the cost of power indefinitely.

Inside the Circuits: Understanding Learned Algorithms

Because these circuits are so compact, the researchers could manually trace their computations—reverse-engineering them to human-level understanding. Three examples stand out.

Circuit 1: How a Model Closes Strings

The task: Given an opening quote (' or ") in Python code, predict the matching closing quote.

The discovered circuit uses only 12 nodes and 9 edges, operating in two conceptual stages:

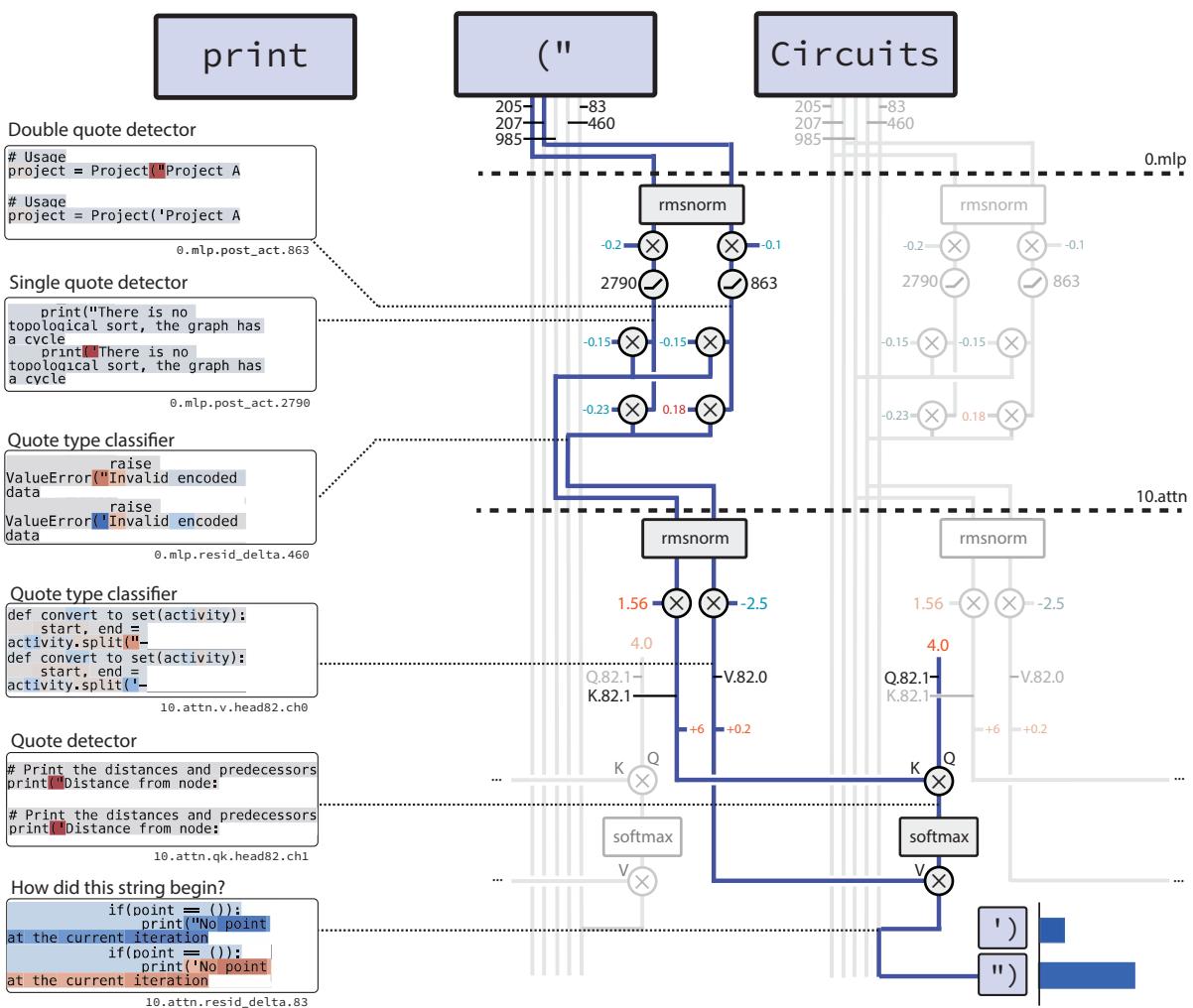
A detailed diagram of the string-closing circuit, showing how token embeddings are processed by an MLP and then used by an attention head to predict the correct closing quote.

Figure 4. The string-closing circuit: two neurons detect and classify quotes, and one attention head copies the correct quote type forward.

  1. Detection: The first MLP layer transforms token embeddings into two specialized signals:
  • A quote detector neuron, which fires for any quote mark.
  • A quote type classifier, positive for double quotes and negative for single quotes.
  1. Copying: Later, an attention head uses these signals to generate the correct closing quote. The detector acts as a key (telling the head which token to attend to), while the classifier acts as the value (encoding quote type). The output directly reflects the correct closing character.

This precise, step-by-step behavior mirrors the explicit algorithm humans would design to close string literals.

Circuit 2: Counting Nested Lists

The task: Predict whether to close a list with ] or ]], depending on nesting depth.

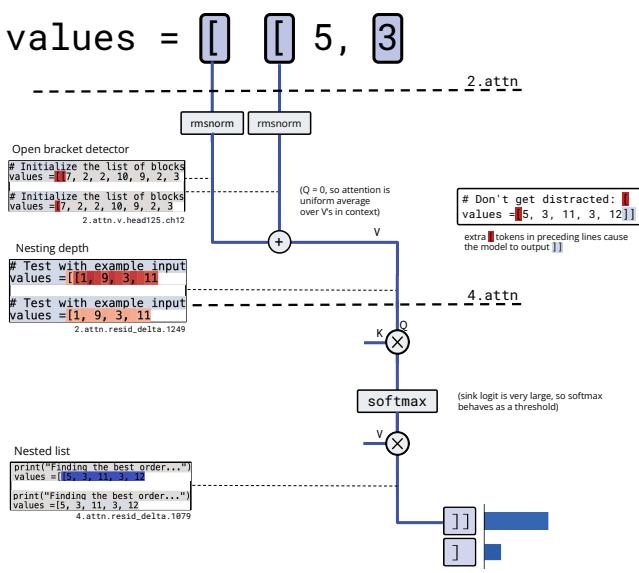
A simplified diagram of the bracket-counting circuit. It shows an “open bracket detector” being averaged over context to create a “nesting depth” signal, which is then thresholded.

Figure 5. The bracket-counting circuit: detects open brackets, averages their representation to encode nesting depth, and thresholds it to decide between ] and ]].

The circuit operates in three distinct stages:

  1. Detection: An attention value channel acts as an “open bracket detector” whenever the model sees [.

  2. Counting by Averaging: A subsequent attention head has nearly constant queries and keys. This effectively averages the “open bracket detector” values over the context, writing the mean activation into the residual stream — a representation of nesting depth.

  3. Thresholding: Another head reads the nesting depth signal and applies a softmax threshold: high activations for deeply nested lists trigger ]], while shallow activations yield ].

Understanding this algorithm enabled the researchers to predict—and create—adversarial failures. Long sequences dilute the average activation, lowering nesting depth and causing the model to incorrectly predict a single closing bracket.

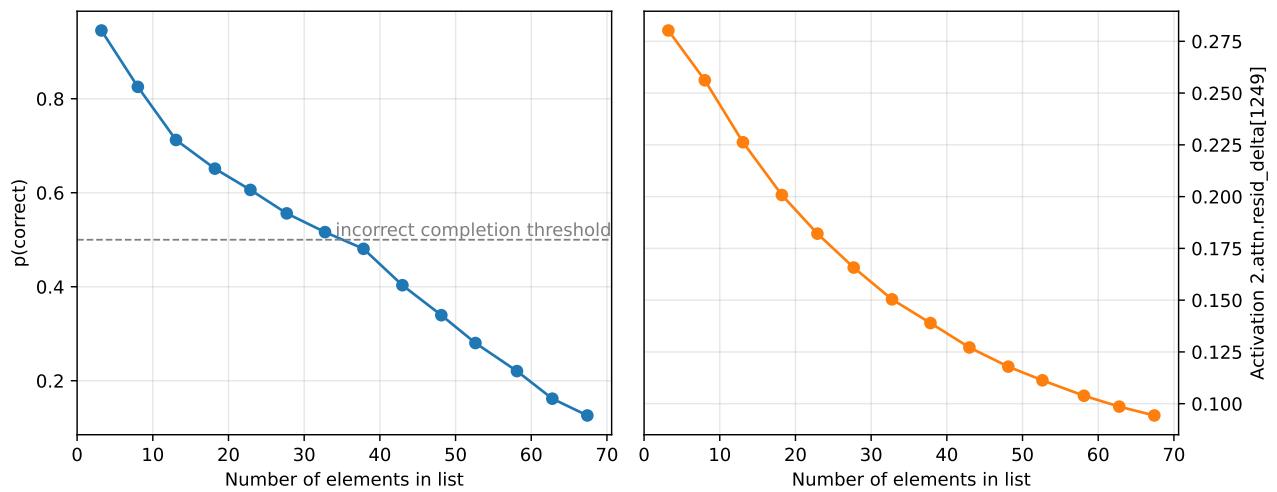
A chart showing that as the number of elements in a list increases, the model’s accuracy on predicting the correct closing bracket drops, perfectly correlated with the decreasing activation of the “nesting depth” feature.

Figure 8. As the list grows longer, “context dilution” weakens the nesting-depth signal and lowers accuracy—demonstrating predictive power from circuit-level understanding.

Circuit 3: Tracking Variable Types

The task: Decide whether a variable was initialized as a set() or a string, selecting between .add and +=.

A schematic of the two-hop attention circuit used for tracking a variable’s type.

Figure 6. The variable-type tracking circuit: a two-hop algorithm copies type information across tokens and retrieves it later.

This circuit uses two attention heads and performs a simple information lookup algorithm:

  1. Hop 1: The first head copies the variable name (current) into the context of its initialization (set()), effectively “tagging” the type with that name.
  2. Hop 2: When the model later encounters current, a second head retrieves the tagged information from set() and copies it forward, allowing correct method completion.

Even complex symbolic tracking behaviors emerge naturally from interpretable sparse computations.

Bridging Sparse and Dense Models

While sparse models offer clarity, they’re costly to train and inherently inefficient. A key question remains: can these insights help us understand existing dense models?

A diagram showing a dense model and a sparse model being trained jointly with “bridge” layers connecting their internal representations.

Figure 7. Bridges connect layers of dense and sparse models, aligning their internal activations to allow interpretable transfer.

To answer this, the researchers introduced bridges—linear mappings trained between corresponding layers of a dense model and a sparse model. These bridges allow activations to be translated back and forth, effectively pairing dense and interpretable representations.

Through this setup, perturbations applied to interpretable channels in the sparse model can be projected into the dense model, steering its behavior predictably.

Two plots showing how steering activations in the sparse model, via the bridge, can successfully and predictably alter the output probabilities of the dense model.

Figure 9. Controlled edits via sparse–dense bridges show how interpretable activations can steer dense models’ outputs.

For instance, manipulating the “quote type classifier” neuron in the sparse model and projecting it into the dense version increased the dense model’s probability of outputting a single quote. This indicates potential alignment between the two architectures—a first step toward decoding the dense networks we already rely on.

Looking Ahead: Toward Transparent Intelligence

This work marks a transformative step toward making AI systems comprehensible. By training weight-sparse models, the researchers created transformers whose reasoning can be fully traced, at the level of individual connections. They demonstrated clear, mechanistic algorithms for language tasks — something rarely achievable in standard models.

However, the method remains computationally expensive. Sparse models require far more training resources than dense ones, making them impractical at scale. Future progress will likely come from two directions:

  1. Scaling model organisms: Building progressively larger sparse models—interpretable “model organisms” up to GPT-3 scale—could reveal universal circuit motifs shared across architectures.

  2. Focusing on critical tasks: Using bridged sparse models to study small, high-stakes domains—such as truthfulness or safety-related behaviors in frontier models—could yield practical insight without full retraining.

Ultimately, the promise of sparse circuits lies not only in improved interpretability but in enabling automated understanding. By constructing models whose internal language is clear and structured, we establish the primitives necessary for future AI tools to reason about themselves.

Through work like this, we move one step closer to a world where AI is not a black box but a glass box—powerful and transparent, efficient and interpretable, capable and accountable.