The dream of creating artificial life—digital organisms that are complex, adaptive, and endlessly creative—has captivated scientists for decades. In that pursuit, researchers have typically explored two main paths:
- Evolutionary algorithms, which mimic natural selection to discover novel behaviors. They’re powerful and open-ended but often slow and unguided.
- Gradient-based learning, the cornerstone of deep learning. It’s efficient at optimizing systems with millions of parameters but usually operates within fixed, static objectives.
What if we could combine them? Imagine a system that harnesses deep learning’s optimization power but places it in a dynamic, competitive world—a digital ecosystem where survival and growth drive spontaneous complexity.
That’s the vision behind Petri Dish Neural Cellular Automata (PD-NCA), a new framework from Sakana AI. In PD-NCA, multiple AI agents known as Neural Cellular Automata (NCA) inhabit a shared digital “petri dish,” competing for territory and adapting continuously through gradient descent. The result is a vibrant, differentiable ecosystem showing early signs of emergent cooperation, competition, and life-like complexity.
Let’s explore how this research brings gradient-based learning into the realm of open-ended artificial life.
Background: The Building Blocks of Digital Life
Before diving into the Petri Dish, we need to understand two foundational ideas in ALife: open-endedness and Neural Cellular Automata.
The Quest for Open-Endedness
In artificial life, “open-endedness” refers to a system’s ability to generate novel and increasingly complex behaviors indefinitely. Biological evolution is our best-known example—it didn’t stop after bacteria but continued to produce endlessly diverse forms of life. By contrast, most AI systems are trained to solve one specific task and then stop learning. Achieving open-endedness—continuous creative growth—is considered one of the “last grand challenges” of artificial intelligence.
Neural Cellular Automata: Simple Rules, Complex Worlds
A traditional Cellular Automaton (CA) consists of a grid of cells that update based on local rules. The most famous case is Conway’s Game of Life, where simple update rules yield surprisingly intricate patterns.
Neural Cellular Automata (NCA) take this idea further. Proposed in 2020, an NCA replaces the fixed rules with a miniature CNN that learns to govern local updates. For instance, an NCA can learn to “grow” an image from a single seed cell that self-regenerates if damaged—demonstrating that gradient descent can evolve self-organizing behaviors.
Yet these NCAs face limits when viewed through an ALife lens:
- They usually simulate only a single agent.
- Their objectives are fixed (e.g., reproduce a specific image).
PD-NCA extends this concept into a multi-agent world that evolves without static goals.
Inside the Petri Dish: A Multi-Agent Learning World
PD-NCA introduces a differentiable multi-agent substrate—a 2D grid where numerous NCAs coexist, compete, and continuously learn during simulation. Think of it as a digital ecosystem governed not by hard-coded logic but by calculus and adaptation.
Each simulation step unfolds in three phases: Processing, Competition, and State Update.
The Setup: A High-Dimensional Environment
Every cell in the grid holds a state vector composed of multiple channels:
- Attack Channels: Represent offensive strategies.
- Defense Channels: Represent resilience against opponents.
- Hidden Channels: Store internal computations or memory.
Additionally, each NCA maintains a private aliveness channel—a hidden map tracking its territorial influence across the grid.
Phase 1: Processing — Proposing Updates
In the first phase, each NCA surveys its neighborhood through its convolutional network and proposes local state updates—its “intentions” for how cells should change.
These updates are masked by aliveness. An NCA can only act within regions it currently controls or near them, preventing distant interference. The system also adds a static environment vector, a constant background influence that functions like a digital nutrient field—fuel for future growth.
Phase 2: Competition — The Struggle for Existence
When multiple NCAs propose conflicting updates to the same cell, who wins? The answer lies in an elegant mechanism based on attack-and-defense vectors.
Each NCA’s strength at a cell is computed as the sum of cosine similarities between its attack vector and every opponent’s defense vector (including the environment’s):
\[ \text{Strength}_A = \langle \text{attack}_A, \text{defense}_B \rangle + \langle \text{attack}_A, \text{defense}_{env} \rangle \]\[ \text{Strength}_B = \langle \text{attack}_B, \text{defense}_A \rangle + \langle \text{attack}_B, \text{defense}_{env} \rangle \]These raw strengths are passed through a softmax, normalizing them into probabilistic weights that decide whose update dominates.

Figure 2: Competition mechanism between two NCAs. Attack-defense similarities form strength scores that are normalized through a softmax to determine relative influence and aliveness.
This mechanism encourages rich strategic adaptation. NCAs can’t rely on a single powerful attack; they must learn nuanced, flexible behaviors to coexist and thrive amidst evolving adversaries.
Phase 3: State Update — Survival of the Fittest
The State Update phase aggregates all proposed updates. Each cell’s new state is a weighted combination of all NCAs’ proposals, with weights derived from their softmax-normalized strengths.
Importantly, these weights also become the NCAs’ new aliveness values for that cell. If an NCA’s total aliveness across the grid drops below a threshold, it is “extinct,” and its territory redistributes among survivors.
This continuous struggle ensures perpetual adaptation—a hallmark of living systems.
The Objective: A Drive to Grow
Each NCA optimizes a simple self-centered goal—maximize its total aliveness. Formally, the loss for NCA \( i \) is:
\[ L_i = -\log\left(\sum_{x,y} A_i(x,y)\right) \]Here \( A_i(x,y) \) is its aliveness at position \((x,y)\). This formulation stabilizes training while maintaining a natural incentive: expand territory, stay alive.
There’s no train/test division; learning never pauses. Gradient descent is woven directly into the simulation’s ongoing dynamics. The agents learn as they live.
What Emerged: Life in the Digital Dish
The researchers trained PD-NCAs on \(256 \times 256\) grids, with CNNs containing up to 500,000 parameters and up to 15 competing agents. The outcomes were striking—far from static or trivial.
Instead of monotonic domination by one “species,” PD-NCAs produced a kaleidoscope of emergent patterns: symbioses, oscillations, and continuous coexistence.
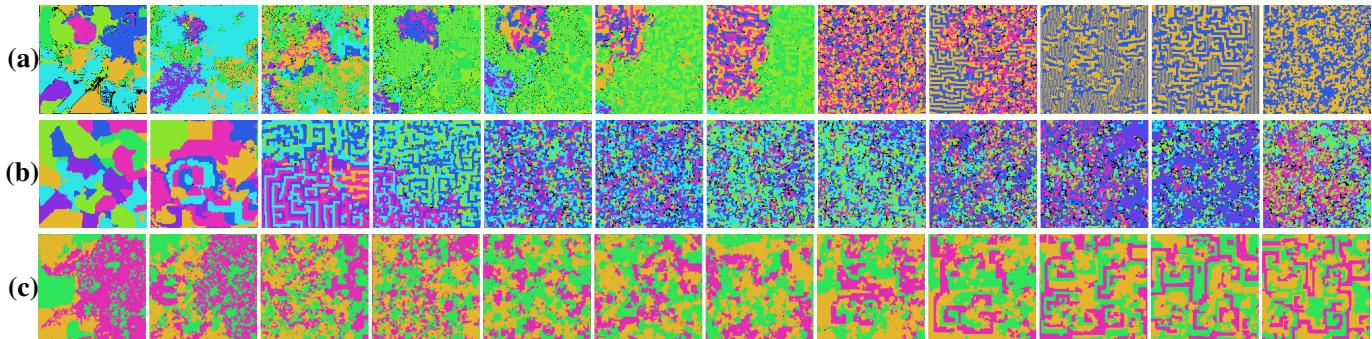
Figure 1: Signs of emergent complexity in PD-NCA simulations. Structured pairings (a), stable competition (b), and wave-like patterns (c) demonstrate spontaneous self-organization.
Symbiosis and Alliances
In simulations, pairs of NCAs often formed stable boundaries, seemingly cooperating to maintain mutual borders. Cyan-purple and blue-orange groups, for instance, coexisted peacefully while fending off other adversaries—an unexpected digital symbiosis.
Dynamic Equilibria
Rather than collapsing into a single winner, many simulations reached a balanced competition, with multiple persistent species. This continuous flux mirrors ecological balance in natural environments.
Wave-like Patterns
Some experiments generated mesmerizing spiral dynamics reminiscent of oscillatory chemical reactions like the Belousov–Zhabotinsky process. Such behavior points to the PD-NCA’s potential as a substrate for complex spatiotemporal phenomena.
Population Dynamics: The Rise and Fall of Digital Empires
To quantify these intricate interactions, the researchers plotted each NCA’s territory size over time. The result: fluctuating waves of competition and cooperation.

Figure 3: Territory size dynamics showing oscillations and cooperative behavior between NCA pairs.
The graph paints a living ecosystem—territories expanding and collapsing in rhythmic cycles. Some NCA pairs rise and fall together, hinting at mutual reinforcement. These quantitative traces echo the visual evidence of alliances and coexistence found in Figure 1.
Towards Open-Ended Digital Evolution
PD-NCA provides a fresh, differentiable foundation for studying artificial life. By embedding continuous learning into a multi-agent competitive substrate, it bridges deep learning and open-ended evolution.
The authors outline several exciting extensions:
- Hybrid Learning-Evolution Systems: When an NCA’s territory splits, each fragment could evolve independently with its own optimizer—combining local gradient-based adaptation with evolutionary diversification.
- Global Objectives: The system, being fully differentiable, could include global rewards—for instance, encouraging ecosystem-wide compressibility or collective problem-solving.
- Automated Substrate Discovery: Using tools like ASAL, meta-models might discover new underlying physics—the rules of competition and cooperation themselves—accelerating the emergence of novel life-like phenomena.
Conclusion: Growing, Not Building, Artificial Life
Petri Dish NCA marks a conceptual shift. It doesn’t simulate evolution or train agents in isolation—it grows them continuously within a shared differentiable world.
From simple local rules and the drive to expand, we see spontaneous emergence of cooperation, competition, and self-organized complexity—the very principles that shape biological ecosystems.
By merging learning and evolution, PD-NCA opens a new frontier for artificial life research. It invites us to create not predefined machines but growing, adapting digital organisms—a computational primordial soup where intelligence and life might evolve side by side.
