在机器学习中，我们在开始训练模型之前经常面临一个“金发姑娘”式的两难境地: 模型应该有多大？

如果模型太小 (神经元太少，参数太少) ，它无法捕捉数据的复杂性，导致预测效果差。如果模型太大，则会浪费计算资源、内存和能源，却不会带来任何额外的准确性提升。在拥有硬盘上所有训练数据的标准设置下，你可以通过交叉验证来解决这个问题——尝试不同的大小并选择最好的一个。

但是如果你还没有数据怎么办？

在持续学习 (Continual Learning) 中，数据以永无止境的流式到达。模型必须即时学习，并在处理后立即丢弃数据以节省内存。你无法预知未来数据集最终会变得多么复杂。这使得设定固定的模型大小几乎是不可能的。

在这篇文章中，我们将深入探讨一篇研究论文，它利用高斯过程 (Gaussian Processes, GPs) 为这个问题提出了一个优雅的解决方案。研究人员介绍了一种名为 VIPS (Vegas Inducing Point Selection，维加斯诱导点选择) 的方法，该方法允许模型在学习过程的每一步自动决定“多大才算足够大”。

持续学习的挑战

传统的机器学习假设数据集是静态的。训练，测试，部署。持续学习颠覆了这个剧本。想象一个机器人在探索新环境，或者一个传感器网络在监测气候数据。数据分批到达，可能会永远持续下去。

这引入了两个主要障碍:

  1. 灾难性遗忘 (Catastrophic Forgetting) : 当模型学习新信息时，它倾向于覆盖并忘记以前学到的东西。
  2. 容量选择 (Capacity Selection) : 既然我们不知道机器人是会探索一个简单的方形房间还是一个复杂的迷宫，我们就不知道模型需要多少“记忆” (容量) 。

如果为了安全起见我们分配巨大的固定容量，我们可能会在处理简单数据时耗尽计算预算。如果分配太少，当环境变复杂时机器人就会停止学习。理想的解决方案是一个自适应增长的模型——仅在数据有需求时扩展其容量。

高斯过程: 无限网络

要理解这个解决方案，我们需要先看看所使用的模型架构: 高斯过程 (GPs) 。

虽然深度神经网络由有限数量的神经元定义，但高斯过程在数学上等同于拥有无限数量神经元的神经网络。这一特性使得 GP 在捕捉复杂函数和提供不确定性估计 (知道自己何时不知道某事) 方面非常强大。

然而，你不能在有限的计算机上计算无限的模型。为了使 GP 实用化，我们使用稀疏变分 GP (Sparse Variational GPs) 。

稀疏近似

我们不使用所有数据点来定义函数 (因为这会呈立方级增长，\(O(N^3)\)，使得处理大数据流成为不可能) ，稀疏 GP 使用一组较小的伪点 (pseudo-points) 来概括数据，这些点被称为诱导变量 (或诱导点) 。把这些点想象成支撑函数形状的“支柱”。

这种近似的数学公式如下所示:

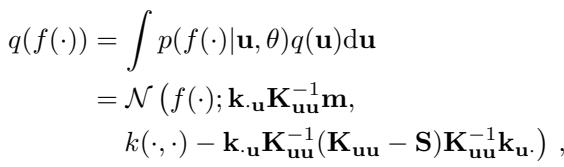
Equation for the variational distribution q(f).

这里，\(M\) 是诱导点的数量。模型的质量几乎完全取决于 \(M\)。

  • 低 \(M\): 模型速度快但模糊；会遗漏细节。
  • 高 \(M\): 模型准确但速度慢且占用内存。

在标准方法中，\(M\) 是由人选择的固定超参数。这项研究的目标是让 \(M\) 变为动态的。

VIPS: 一种用于模型定径的“拉斯维加斯”算法

研究人员提出了 VIPS (Vegas Inducing Point Selection) 。这个名字是对“拉斯维加斯算法”的致敬——这类随机算法总是能产生正确的结果 (满足特定条件) ，尽管产生结果所需的时间可能会有所不同。

VIPS 的核心思想简单而深刻: 不断添加诱导点，直到模型与理论上的最优模型相比“足够好”。

理论差距

为了确定模型是否足够好，我们需要一个指标。在贝叶斯推断中，我们通常最大化 ELBO (证据下界) 。 ELBO 在数据拟合度和模型复杂度之间取得平衡。

研究人员推导出了一种方法来测量模型当前性能 (下界) 与最佳可能理论性能 (上界) 之间的差距。

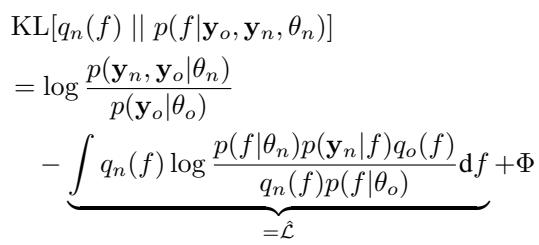
The breakdown of the KL divergence showing the online ELBO.

这个方程展示了 Kullback-Leibler (KL) 散度，它衡量我们的近似分布与真实后验分布之间的距离。我们无法精确计算真实的后验分布，但我们可以确定误差的界限。

算法

VIPS 算法对每一个新到达的数据批次进行操作。它遵循一个贪婪过程:

  1. 评估 (Assess) : 计算当前的下界 (我们做得有多好) 和上界 (我们可能做得多好) 。
  2. 检查 (Check) : 它们之间的差距是否足够小？
  3. 行动 (Act) : 如果差距太大，找出当前批次中模型最“困惑” (方差最大) 的数据点。将该数据点转变为新的诱导点。
  4. 重复 (Repeat) : 重新计算并重复，直到差距闭合。

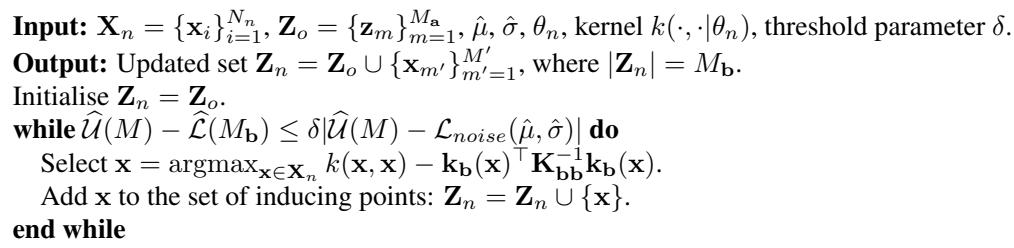
Algorithm 1: Vegas Inducing Point Selection (VIPS).

这种方法确保了我们只在模型真正难以表示新数据时才增加容量。如果新数据是冗余的 (与我们之前见过的相似) ，差距会很小，模型大小就不会增长。

停止阈值

关键问题是: 阈值是多少？如果我们设定的容差太紧，模型就会不断添加点，直到基本上记住了数据集 (过度拟合且变得太大) 。

作者建议使用一个相对于噪声模型的阈值。我们希望捕捉信号中的大部分信息，但不需要对随机噪声建模。

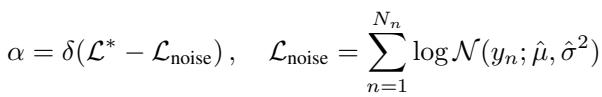
Equation for the adaptive threshold alpha based on noise.

通过根据数据的噪声水平设定阈值 \(\alpha\)，该方法变得稳健。它适用于高信噪比的数据集和噪声很大的数据集，而无需为每个新问题手动调整。

可视化自适应增长

为了观察 VIPS 的实际效果，让我们看看三种不同的合成场景。这个可视化完美地说明了为什么“一刀切”的固定模型会失败。

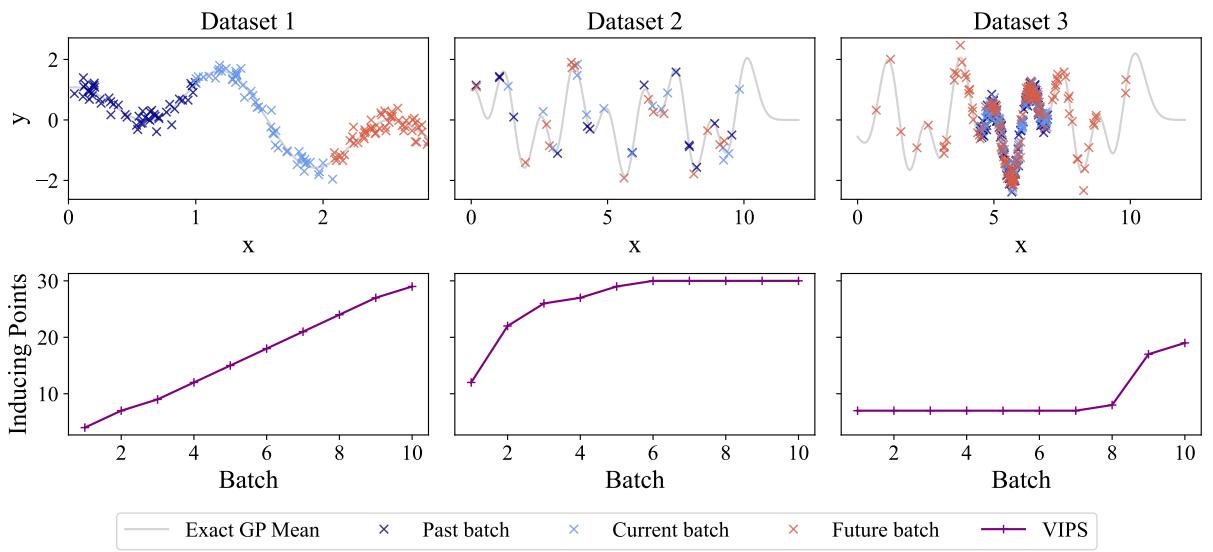
Three continual learning scenarios with different capacity requirements. Top: Data distribution. Bottom: Number of inducing points selected by VIPS.

  1. 场景 1 (左) : 输入空间不断增长 (x轴扩展) 。模型不断遇到新数据。VIPS 的反应是线性增加诱导点的数量。一个固定大小的模型会在中途耗尽容量。
  2. 场景 2 (中) : 数据反复来自同一区域。在初始学习阶段之后，新数据并没有增加太多“新颖性”。VIPS 正确地识别了这一点并停止增长 , 从而节省了计算资源。在这里使用“每批次增加10个点”的启发式方法将会是浪费。
  3. 场景 3 (右) : 数据大多很简单，但偶尔会有异常值 (红色叉号) 出现在新区域。VIPS 在简单阶段保持模型较小，但在需要捕捉异常值时立即激增大小 。

实验结果

这个理论经得起基准测试和现实任务的考验吗？研究人员将 VIPS 与固定大小的方法以及其他自适应算法 (如“条件方差”即 CV，和 OIPS) 进行了比较。

固定 vs. 自适应

首先，让我们看看猜测固定大小的风险。

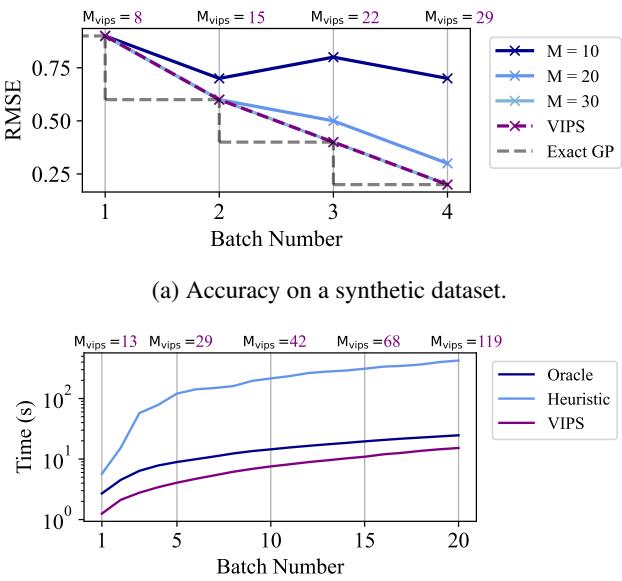
(a) Accuracy comparison of fixed memory approaches vs VIPS. (b) Training time comparison.

在 图 2(a) 中，请注意蓝线。如果你选择 \(M=10\) 或 \(M=20\) (固定大小) ，误差 (RMSE) 在一段时间内会改善，但随后会停滞或变差，因为模型“满”了。紫色线 (VIPS) 会自动增长以匹配精确 GP (理论上限) 的性能。

在 图 2(b) 中，看看训练时间。“Oracle” (事先知道完美大小的人) 设定 \(M=100\)。标准的启发式方法设定 \(M=1000\) (为了安全起见) 。VIPS (紫色) 比启发式方法快，且与 Oracle 相当，因为它没有在早期批次中浪费时间计算不必要的参数。

跨数据集的稳健性

该论文的一个主要主张是 VIPS 需要更少的调优。在持续学习中，你通常无法调整超参数，因为你无法重播数据流。你需要一个能够“开箱即用”的设置。

研究人员在几个 UCI 基准数据集上测试了 VIPS。他们统计了每种方法在满足严格准确度阈值的同时达到最小模型大小的频率。

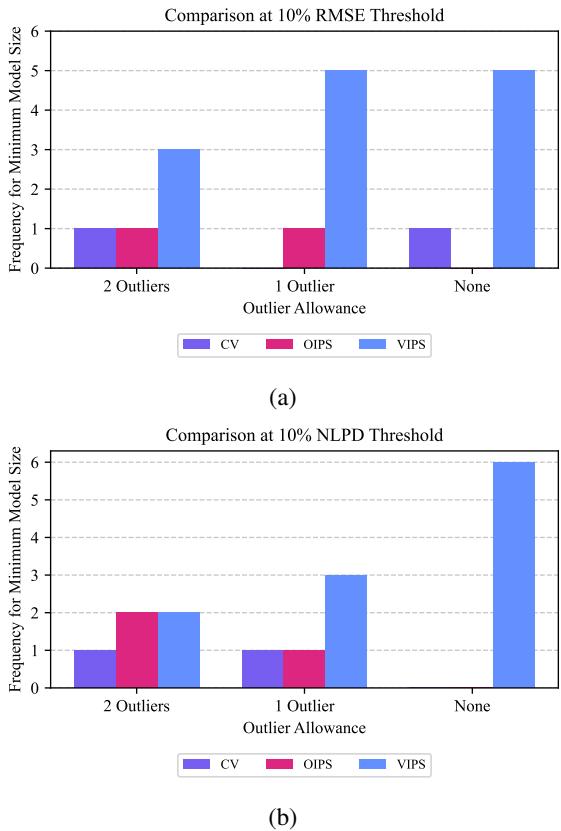
Bar charts showing the number of datasets where each method achieves minimal model size.

蓝色条代表 VIPS。在不同的误差容限 (RMSE 和 NLPD) 下，VIPS 始终获得“胜利”——意味着它比竞争对手 (CV 和 OIPS) 更频繁地找到最高效的模型大小。这表明当你无法预先知道数据集特征时，使用 VIPS 更安全。

现实世界应用: 机器人测绘

最令人信服的演示涉及一个机器人在房间内探索以绘制磁场异常图。这是一个经典的持续学习设置: 机器人行驶，收集数据，并更新其地图。在到达那里之前，它不知道磁场有多复杂。

让我们看看由 VIPS 生成的地图:

VIPS estimate of magnetic field anomalies. Points represent inducing points.

在 图 8 中，黑点代表 VIPS 选择的诱导点。注意点的数量 (\(M\)) 随着机器人行驶复杂路径从 5 稳定增长到 134。模型在路径蜿蜒曲折 (高复杂度) 的地方密集放置点，而在路径笔直的地方稀疏放置。

现在，将其与竞争方法 条件方差 (CV) 进行比较:

Conditional Variance estimate. Note the massive number of inducing points (M).

在 图 10 中，条件方差方法的复杂度呈爆炸式增长。到了第 20 批次，它选择了 5,785 个诱导点 ! 这对小型机器人来说是计算灾难。无论是否有必要，它都在到处添加点。

在另一个极端，让我们看看 OIPS :

OIPS estimate. Note the sparsity and potential lack of detail.

在 图 12 中，OIPS 过于保守。它只选择了 76 个点。虽然效率高，但这篇论文之前的基准测试表明，OIPS 经常无法达到准确度阈值，因为它停止增长得太早了。

VIPS 达到了“金发姑娘”式的平衡: 点数足够多以保证准确 (像全量 GP 一样) ，但又足够少以在机器人上进行计算是可行的。

结论

“多大才算足够大？”这个问题是高效机器学习的核心。这项研究为高斯过程提供了一个原则性的答案。通过在数学上限定当前近似与最优解之间的差异, VIPS 允许模型自我调节其大小。

关键要点:

  1. 效率 (Efficiency) : VIPS 在学习新概念时线性增长，但在数据变得重复时停滞增长。
  2. 安全性 (Safety) : 与启发式方法不同，它对近似质量有理论保证。
  3. 实用性 (Practicality) : 它通过单个超参数在各种数据集上表现良好，解决了流式数据中无法调优的主要痛点。

虽然这篇论文侧重于高斯过程，但将模型容量与近似质量分离的原则为更广泛的深度学习领域提供了令人兴奋的方向。随着我们迈向在现实世界中持续学习的 AI 智能体，像 VIPS 这样的自适应容量方法将是保持它们智能而又不烧毁处理器的关键。