复杂查询问答中的进步假象

在人工智能领域，圣杯之一就是复杂推理 。 我们不仅想要机器能识别图片中的猫，还希望系统能通过复杂的逻辑链来回答需要多步骤的问题。

在知识图谱 (KGs) 领域，这项任务被称为复杂查询问答 (Complex Query Answering, CQA) 。 多年来，研究人员一直在开发神经网络，将查询和实体映射到潜在空间，旨在解决复杂的逻辑难题。如果你查看 FB15k-237 或 NELL995 等标准基准的排行榜，看起来我们正在取得令人难以置信的进步。准确率在上升，模型似乎正在掌握推理能力。

但最近一篇题为 “Is Complex Query Answering Really Complex?” (复杂查询问答真的复杂吗？) 的论文给这种说法投下了一枚重磅炸弹。作者认为，我们所感知的进步很大程度上是由于我们构建基准测试的方式所造成的假象。事实证明，我们用来测试 AI 的“复杂”查询实际上是伪装成难题的“简单”问题，这使得模型可以通过记忆训练数据作弊，而不是学习推理。

在本文中，我们将解构这项研究，解释为什么当前的基准存在缺陷，并探讨作者提出的全新且真正具有挑战性的标准。

背景: 知识图谱与逻辑查询

要理解这个缺陷，我们首先需要理解这项任务。 知识图谱 (KG) 是一种使用实体 (节点) 和关系 (边) 存储数据的结构化方式。例如，一个三元组可能看起来像 (Spiderman 2, distributedVia, Blue Ray)。

CQA 的目标

CQA 涉及在这些图谱上回答一阶逻辑问题。这些不是简单的查找；它们涉及合取 (AND) 、析取 (OR) 、否定 (NOT) 和存在量化等逻辑运算符。

考虑以下自然语言查询:

“哪位演员出演过一部既在纽约市拍摄又以蓝光形式发行的电影？”

用逻辑术语来说，找到答案 (目标 \(T\)) 涉及找到一个同时满足三个条件的变量 \(V\) (电影) :

  1. 电影以蓝光形式发行。
  2. 电影在纽约市拍摄。
  3. 该演员出演了那部电影。

查询类型

在研究中，这些逻辑结构按其形状进行分类。

  • 1p (One Path): 简单的链接预测。给定实体 A 和关系 R，预测实体 B。
  • 2p / 3p: 多跳路径 (A → B → C) 。
  • 2i / 3i: 交集。寻找连接到 2 个或 3 个其他特定实体的实体。
  • 2u: 并集 (逻辑 OR) 。

下图展示了这些结构。节点是圆圈，箭头是关系。“i”代表交集，“p”代表路径，“u”代表并集。

包含路径、交集和并集结构的查询结构。

一直以来的假设是, 3p 查询 (3 跳) 比 1p 查询难，而 2i 查询 (交集) 需要复杂的逻辑来聚合来自不同分支的信息。

核心问题: 难度谱系

论文的核心论点是: 结构复杂性不等于推理难度。

标准基准测试通过将知识图谱划分为训练图 (\(G_{train}\)) 和测试图 (\(G_{test}\)) 来工作。目标是在测试图上回答查询，预测缺失的链接。

然而，作者指出，在现实场景 (以及这些基准测试) 中，答案路径的部分内容可能已经存在于训练数据中。这就引出了推理树 (Reasoning Tree) 的概念。

推理树与可归约性

当模型尝试回答查询时，它会遍历从锚实体 (例如“Blue Ray”，“NYC”) 到目标的“推理树”。查询的难度完全取决于树中有多少链接是缺失的 (需要推理) ，以及有多少链接是已观测到的 (存在于训练数据中) 。

如果一个“复杂”查询主要由模型在训练期间已经见过的链接组成，模型就不需要执行复杂的多跳推理。它可以“短路”逻辑。

让我们看一个使用前面讨论过的查询的具体例子:

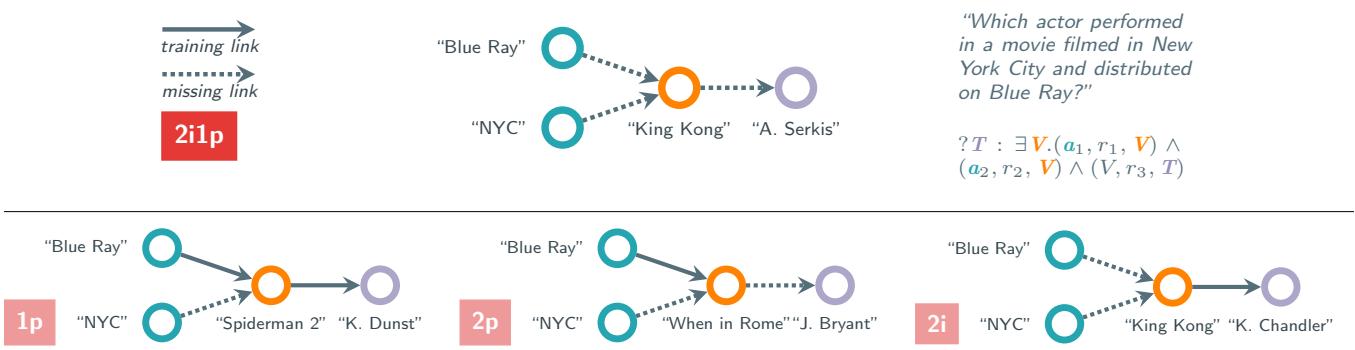
同一查询类型的推理树对比，展示了不同的难度级别。

如图 1 所示:

  1. 上方情况 (全推理) : 为了找到答案 “A. Serkis”，模型必须预测从 Blue Ray 到 King Kong，以及从 NYC 到 King Kong，以及从 King Kong 到 A. Serkis 的链接。所有链接都是缺失的 (虚线) 。这是一个困难的查询。
  2. 下方情况 (部分推理) : 为了找到 “K. Dunst”，模型看到在训练数据中 “Spiderman 2” 已经连接到了 “Blue Ray” (实线) 。模型不需要推断这种关系；它只需要查找即可。复杂的 “2i1p” 查询实际上坍缩成了从 Spiderman 2 到 K. Dunst 的简单 “1p” (链接预测) 查询。

作者正式定义了这种区别:

  • 全推理对 (Full-Inference Pair) : 一个查询/答案对，其推理树完全由仅在测试集中发现的链接组成。模型必须对每一步都在未见过的数据上进行推理。
  • 部分推理对 (Partial-Inference Pair) : 推理树中至少有一个链接存在于训练集中的对。

令人震惊的统计数据

如果基准是平衡的，我们会期望看到两者的混合。然而，作者分析了流行的 FB15k237 和 NELL995 数据集，发现了巨大的不平衡。

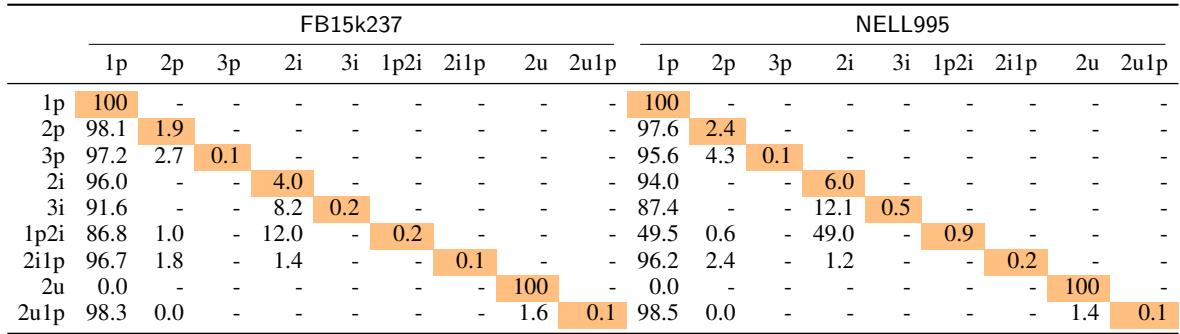
表格显示了可归约为更简单类型的查询百分比。

表 1 揭示了问题的严重程度。看一眼 FB15k237 的 “1p” 列。

  • 对于 2p 查询, 98.1% 可以归约为简单的 1p 查询。
  • 对于 2i1p 查询, 96.7% 可以归约为 1p。
  • 对于 3p 查询, 97.2% 可以归约为 1p。

这意味着对于绝大多数“复杂”查询，模型只需要预测一个单一的缺失链接 。 路径的其余部分是从训练集中记忆下来的。我们不是在测试复杂推理；我们是在测试包装在复杂外壳下的简单链接预测。

为什么当前模型表现“良好”

部分推理查询的普遍存在解释了为什么当前的最新技术 (SoTA) 模型得分很高。神经网络非常擅长记忆训练数据。如果一个模型可以记忆 \(G_{train}\) 并执行不错的单跳链接预测，它就能在这些基准测试中获得高分，而无需执行多跳推理。

为了证明这一点，作者用一个名为 CQD-Hybrid 的“作弊”模型进行了实验。

CQD-Hybrid 实验

CQD (连续查询分解) 是一种现有的神经方法。作者对其进行了修改，创建了一个混合求解器，该求解器:

  1. 使用标准的神经链接预测器。
  2. 显式记忆训练图谱。如果链接存在于 \(G_{train}\) 中，则为其分配最高分 (完美概率) 。

如果真的需要复杂推理 (推断缺失路径) ，这种简单的启发式方法在困难测试集上应该没有太大帮助。但由于测试集充满了“可归约”的查询, CQD-Hybrid 取得了 SOTA 结果 , 在旧基准上优于像 Transformer 和图神经网络这样复杂的专用推理架构。

这证实了假设: 当前基准测试的高性能是由记忆驱动的，而不是推理。

并集 (OR) 谬误

论文还强调了并集 (2u) 查询中的一个致命缺陷。如果满足条件 A 或条件 B，则并集查询 \(A \lor B\) 得到满足。

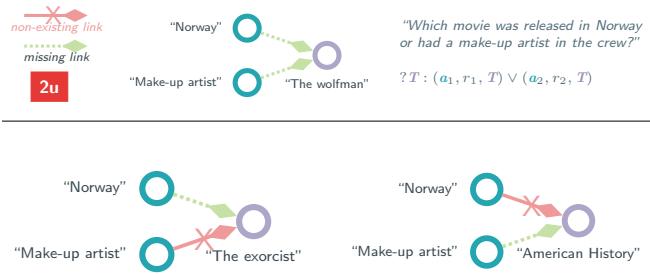
图表展示了有效与无效的并集查询推理树。

如图 3 所示，作者发现许多基准查询中，其中一个分支 (例如通往“The Exorcist”的路径) 依赖于一个图谱中根本不存在的链接 (既不在训练集也不在测试集) 。

如果“OR”查询的一个分支是不可能的，那么该查询实际上就变成了有效分支上的简单 1p 查询。作者发现，过滤掉这些损坏的查询 (只保留两个分支在理论上都可能的查询) 会显著改变感知的难度。

解决方案: 新基准测试 (+H)

为了衡量 AI 推理的实际进展，我们需要不能仅靠记忆解决的基准。作者介绍了三个新数据集:

  1. FB15k237+H
  2. NELL995+H
  3. ICEWS18+H (一个时序知识图谱)

"+H" 代表 Hard (困难，或者也许是 Honest/诚实) 。

它们是如何构建的

这些基准的核心创新在于平衡 。 作者明确地采样查询，以确保“简单” (可归约) 和“困难” (全推理) 查询的分布相等。

  • 对于 3 跳查询类型，基准包含数量相等的归约为 1 跳、2 跳和全 3 跳推理的对。
  • 他们过滤掉了损坏的并集查询。
  • 他们添加了真正深度的查询类型: 4p (4 跳路径) 和 4i (4 路交集) 。

ICEWS18+H: 现实挑战

大多数基准随机分割数据。作者认为这不切实际。在 ICEWS18+H 中，他们使用了基于时间的分割。\(G_{train}\) 包含过去的事件，\(G_{test}\) 包含未来的事件。这使得记忆的效果大打折扣，因为未来的结构可能演变得与过去不同。

结论: SoTA 模型举步维艰

当作者在这些新基准上重新评估当前的顶级模型 (如 GNN-QE、CQD 和基于 Transformer 的模型) 时，结果截然不同。

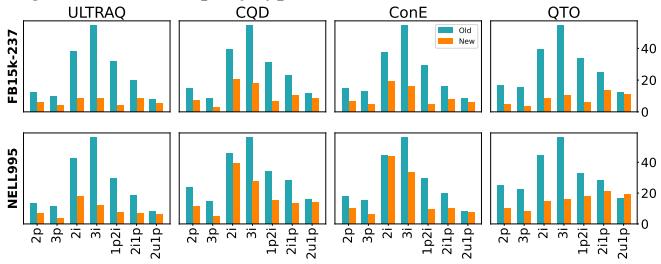
旧基准与新基准上的 MRR 分数对比，显示性能显著下降。

图 4 直观地展示了性能的崩塌。

  • 蓝色柱 (旧基准) : 高性能，暗示掌握了推理能力。
  • 橙色柱 (新基准) : 性能暴跌。

例如，在 FB15k237 的 3i (3 路交集) 查询上，性能 (MRR) 从大约 54.6 下降到了 10.1 。

详细分析

分层分析 (按查询类型细分结果) 彻底说明了这一点。

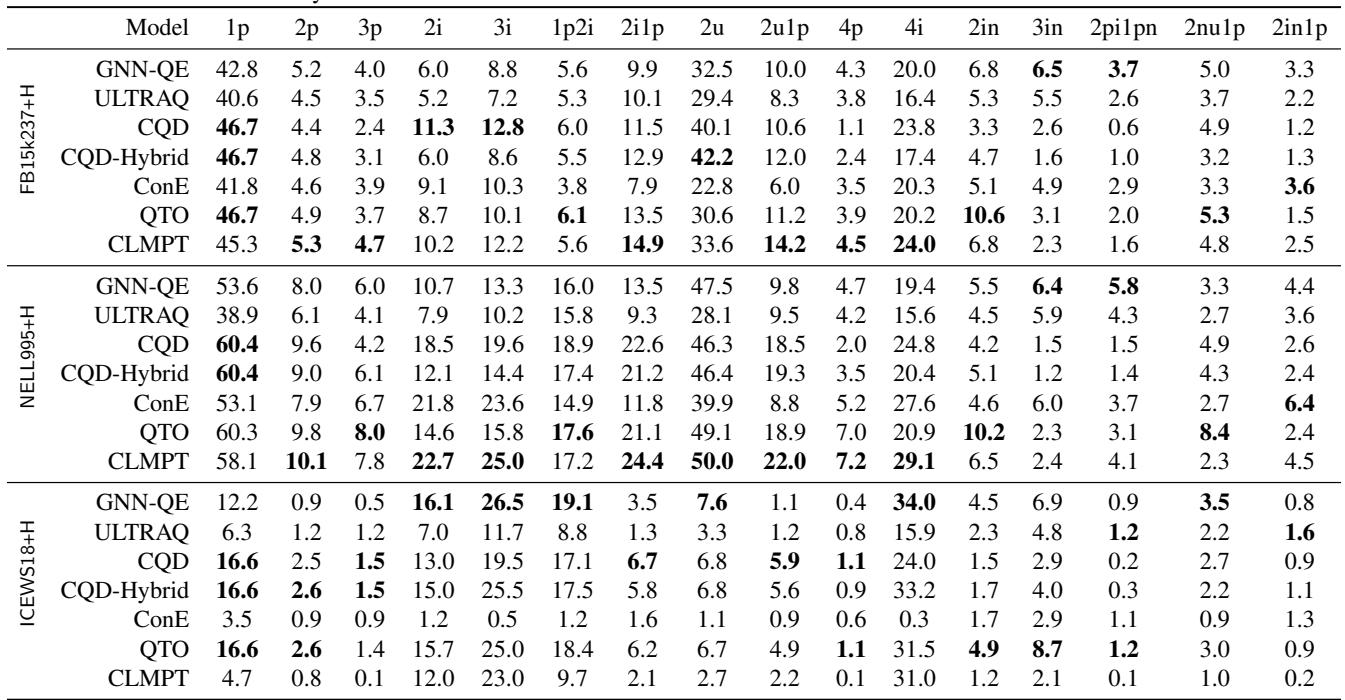
表格显示了在新的平衡基准上的表现。

表 5 显示了新数据集上的结果。再也没有明显的赢家了。在旧基准上占主导地位的模型 (如 QTO) 在新基准上表现极差。简单的 “1p” 查询 (链接预测) 仍然有不错的表现，但一旦查询需要真正的多跳推理 (3p、4p、3i) ，分数就会低得令人难以置信——通常只有个位数。

这表明我们实际上还没有解决全推理复杂查询的可靠方法。 这个问题比我们想象的要难得多。

结论与启示

论文“Is Complex Query Answering Really Complex?”为知识图谱社区敲响了必要的警钟。它证明了:

  1. 复杂性具有欺骗性: 一个逻辑上看起来很复杂 (\(A \land B \land C\)) 的查询，如果数据的一部分已知，计算上可能微不足道。
  2. 基准测试至关重要: 数据集创建中的采样偏差扭曲了我们对该领域多年的看法，掩盖了模型过度拟合简单实例的事实。
  3. 推理尚未解决: 在新的、平衡的基准 (+H) 上，当前的神经方法无法在缺失数据上执行鲁棒的多跳推理。

通过采用这些新基准，研究社区可以停止在简单问题上追求虚高的分数，并开始应对真正的挑战: 构建能够真正对不完整知识进行推理的 AI，而不仅仅是记忆它。