循环神经网络 (RNN) 是时序计算的主力军。从现代机器学习中 Mamba 等状态空间模型的复兴，到神经科学中认知动力学的建模，RNN 无处不在。我们知道它们确实有效——它们能够捕捉随时间变化的依赖关系，整合信息，并对动态系统进行建模。但在我们的理解中存在一个明显的空白: 我们要并不真正了解它们是如何学习的。

大多数关于 RNN 的理论分析都是在训练之后进行的。这就像试图通过仅仅观察建成后的摩天大楼来理解它是如何建造的一样。要真正理解智能 (无论是人工的还是生物的) 的涌现，我们需要观察建造过程本身: 即学习动力学。

在最近一篇题为 “Learning dynamics in linear recurrent neural networks” (线性循环神经网络中的学习动力学) 的论文中，研究人员 Proca、Dominé、Shanahan 和 Mediano 提供了一个突破性的分析框架。通过聚焦于线性 RNN (LRNN) ，他们剥离了非线性的干扰，揭示了支配这些网络如何从时序数据中学习的基本数学原理。

这篇文章将带你了解他们的推导过程，揭示为什么 RNN 学习某些东西比其他的更快，为什么它们有时会变得不稳定，以及循环的本质如何迫使网络学习丰富的特征，而不是走“懒惰”的捷径。

设置: 定义线性 RNN

为了从数学上分析学习动力学，我们需要一个易于处理的模型。作者专注于线性 RNN。虽然它缺乏深度网络中的激活函数 (如 ReLU 或 Tanh) ，但它保留了核心的结构元素: 随时间演变的隐藏状态。

该模型由一个隐藏状态 \(h_t\) 定义，该状态根据其前一个状态和新的输入 \(x_t\) 进行更新，并最终产生输出 \(\hat{y}\)。

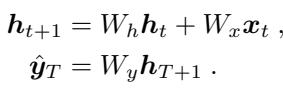
隐藏状态更新和最终输出预测的基本方程。

如果我们随时间展开这个循环，我们会看到任何时刻的隐藏状态都是所有先前输入的总和，这些输入由循环矩阵 \(W_h\) 的幂进行加权。这种指数运算 (\(W_h^{t-i}\)) 是 RNN 的关键特征——它是网络在时间中穿梭的方式。

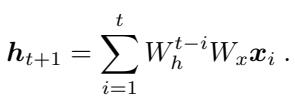
展开后的方程显示隐藏状态是随时间加权的输入的总和。

网络的训练目标是最小化其预测值与目标值之间的平方误差。该损失函数对数据集中的所有轨迹 \(P\) 进行求和。

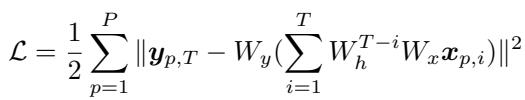
最小化目标值与预测值之间差异的损失函数方程。

任务动力学

这篇论文的关键创新在于作者如何定义“任务”。在线性网络中，任务由输入和输出之间的统计关系定义。作者引入了 任务动力学 (Task Dynamics) 的概念。

他们没有将数据视为静态的整体，而是分解了时间 \(t\) 的输入与最终输出目标之间的相关性。他们利用奇异值分解 (SVD) 来表示这些相关性。

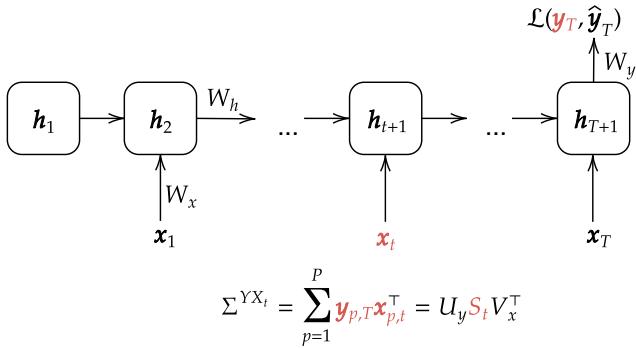
图 1: 随时间展开的 RNN 和任务动力学的 SVD 分解示意图。

如 图 1 所示，输入-输出相关矩阵被分解为奇异向量 (\(U_y, V_x\)) 和奇异值 (\(S_t\)) 。这里的一个关键假设是向量保持不变，但奇异值 (\(S_t\)) 随时间变化。这使得研究人员能够研究网络如何学习“时序结构”——本质上就是输入的重要性如何根据其在序列中出现的时间而变化。

核心方法: 解耦动力学

计算 RNN 的梯度下降动力学通常非常困难，因为参数在所有时间步之间是共享的 (在 \(t=1\) 和 \(t=100\) 时使用的是同一个 \(W_h\)) 。

为了解决这个问题，作者假设网络的权重与数据的奇异向量是“对齐”的。这使得他们可以将矩阵对角化。问题不再涉及庞大的矩阵，而是分解为每个奇异值维度 \(\alpha\) 的独立标量方程。

我们现在可以用三种“连接模式” (代表该维度连接强度的标量值) 来描述网络:

  1. \(a_\alpha\) : 输入模式 (代表 \(W_x\)) 。
  2. \(b_\alpha\) : 循环模式 (代表 \(W_h\)) 。
  3. \(c_\alpha\) : 输出模式 (代表 \(W_y\)) 。

在梯度流 (小学习率的梯度下降) 下，这些模式随训练时间 (\(t_\theta\)) 的演变由一组微分方程控制:

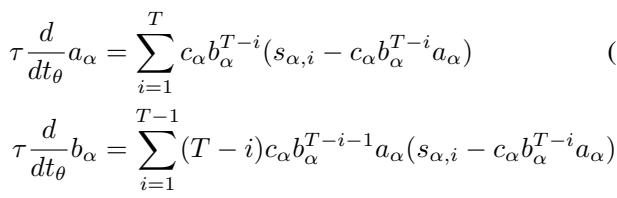
控制输入 (a) 和循环 (b) 模式学习动力学的微分方程。

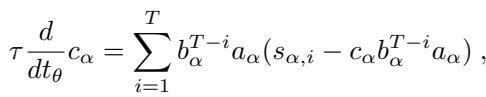
控制输出模式 (c) 学习动力学的微分方程。

这些方程看起来可能有些吓人，但它们揭示了一些迷人的事实。循环模式 \(b\) 的变化 (方程 6) 取决于项 \((T-i)\)。这意味着序列的长度直接影响梯度。

此外，作者证明这些动力学并非随机；它们实际上是在最小化一个特定的 能量函数 :

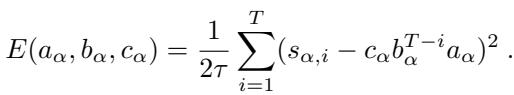
从梯度流推导出的能量函数方程。

这个能量函数 (方程 8) 确切地告诉我们网络试图实现什么。它试图在每个时间步 \(i\)，使其权重的乘积 (\(c \cdot b^{T-i} \cdot a\)) 与数据奇异值 (\(s_i\)) 相匹配。

洞察 1: 时间和尺度决定学习速度

在标准的前馈网络中，我们知道“较大”的奇异值会先被学习。如果一个特征解释了数据中的大量方差，网络就会迅速捕捉到它。

在 RNN 中，情况则更为复杂。作者发现，学习的顺序由 尺度 和 时间优先顺序 共同决定。

为了理解这一点，他们将数据奇异值分解为一个常数缩放因子 (\(\delta\)) 和一个随时间变化的函数 \(f(\lambda, t)\)。

  • 输入-输出模式 (\(a, c\)) 通常学习常数缩放 (\(\delta\)) 。
  • 循环模式 (\(b\)) 学习随时间变化的动力学 (\(\lambda\)) 。

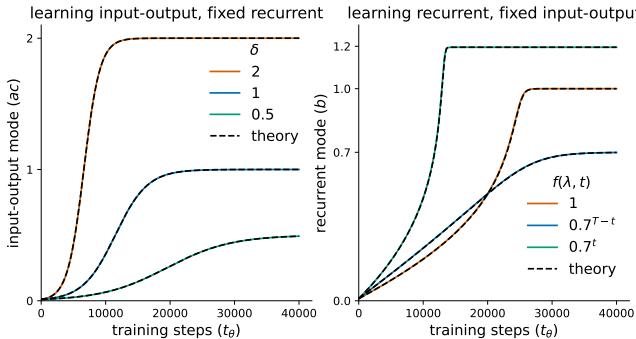
图 2: 显示输入-输出模式与循环模式学习轨迹的图表。

如 图 2 所示，理论 (虚线) 完美地预测了模拟结果 (实线) 。

  • 左图: 输入-输出模式仅仅增长以匹配数据的尺度。较大的 \(\delta\) (橙色线) 学习得更快。
  • 右图: 循环模式学习时序结构。

至关重要的是，作者发现了一种 近因偏差 (Recency Bias) 。 那些较大且出现在序列较晚位置的奇异值会被更快地学习。这是因为循环权重 \(b\) 起到了乘数的作用。如果 \(b\) 开始时很小 (接近 0) ，来自早期时间步的梯度在影响更新之前就会被压缩 (消失) ，而来自近期时间步的梯度则保持强劲。

洞察 2: 稳定性与外推

训练 RNN 最令人头疼的问题之一是稳定性——即避免梯度爆炸。该分析框架为为什么某些任务本质上是不稳定的提供了精确的解释。

研究人员分析了三种特定类型的“任务动力学”:

  1. 常数 (Constant) : 每个输入都同样重要 (\(f(\lambda, t) = 1\)) 。
  2. 逆指数 (Inverse-Exponential) : 重要性随时间增长 (\(f(\lambda, t) = \lambda^{T-t}\)) 。这是“后期重要性”。
  3. 指数 (Exponential) : 重要性随时间衰减 (\(f(\lambda, t) = \lambda^t\)) 。这是“早期重要性”。

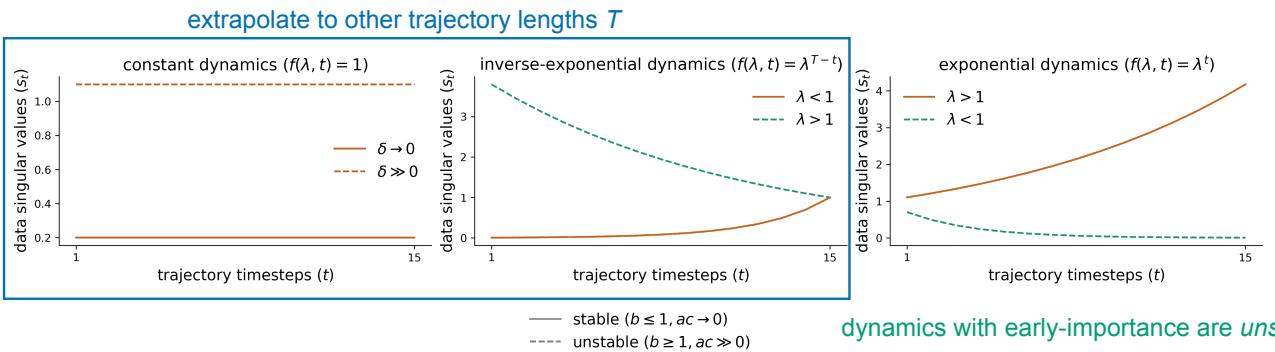
图 3: 不同任务动力学下的稳定性与外推能力的比较。

图 3 展示了这些动力学的后果:

  • 稳定 (中图，橙色) : 当任务具有“后期重要性” (近期的输入最重要) 时，网络学习到的循环权重 \(b \le 1\)。这是稳定的。
  • 不稳定 (右图，橙色) : 当任务具有“早期重要性” (很久以前的输入最重要) 时，网络必须学习到一个 \(b > 1\) 的循环权重来放大那些旧的信号。这会导致梯度爆炸和数值不稳定。

外推陷阱 该分析还解释了为什么 RNN 无法进行外推。请看图 3 中关于指数动力学的注释。输入-输出模式 (\(ac\)) 的最优解取决于序列长度 \(T\)。

\[ac = \delta \lambda^T\]

如果你在长度 \(T=10\) 的序列上训练网络，它会学习到 \(ac\) 的特定值。如果你随后在 \(T=20\) 上进行测试，网络会失败，因为它学到的权重是针对长度 10 硬编码的。RNN 的架构 (假设时间不变的动力学) 与尺度依赖于序列持续时间的任务存在根本性的冲突。

洞察 3: 相变

现实世界的数据很少是完美的。当 RNN 无法完美拟合数据时会发生什么？如果任务需要混合“记住过去” (循环) 和“关注现在” (前馈) 呢？

作者重写了能量函数，揭示了一个隐藏的相互作用:

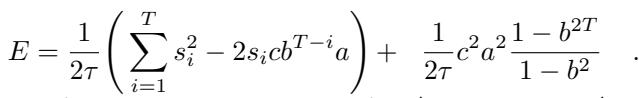
方程 9: 能量函数分解为数据驱动项和有效正则化项。

方程 9 强调了一个 有效正则化项 (Effective Regularization Term) 。 该项惩罚较大的权重，特别是推动循环模式 \(b\) 趋向于零。

这这就产生了一场拉锯战。数据希望网络学习动力学 (增加 \(b\)) ，但这个正则化项希望保持网络简单 (保持 \(b\) 很小) 。这导致了 相变 (Phase Transition) 。

为了演示这一点，作者创建了一个合成任务，在最后一步有一个“前馈”分量 (\(\kappa\)) ，以及由奇异值 \(s_t\) 决定的“循环”分量。

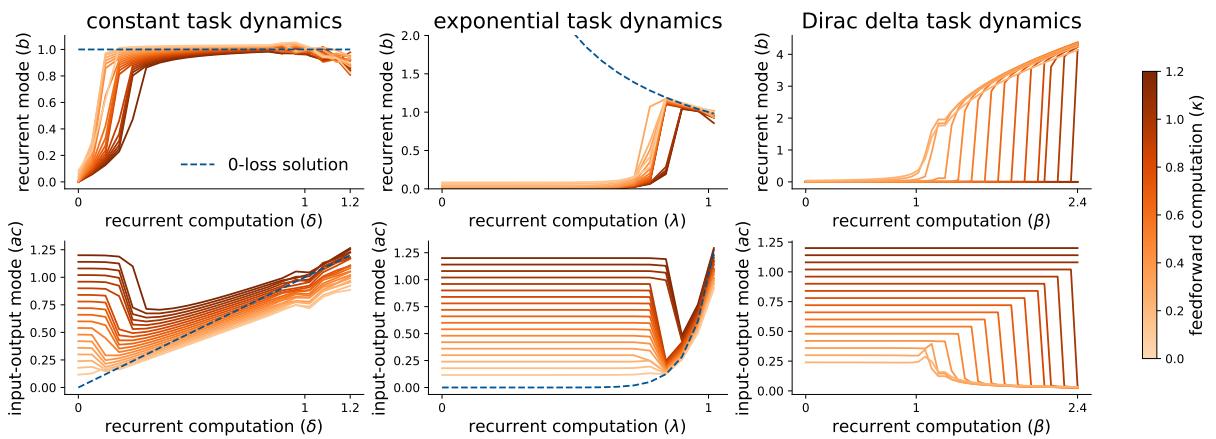
图 4: 展示网络如何在循环解和前馈解之间切换的相变图。

图 4 显示了这种剧烈的行为。

  • 图的左侧: 当循环计算较弱 (X 轴值较低) 时，网络实际上放弃了循环。它将 \(b \approx 0\)，并使用输入-输出权重仅拟合最后的时间步。它的行为就像一个前馈网络。
  • 图的右侧: 随着循环信息变得足够强，网络突然跳入另一种模式。\(b\) 跃升，网络开始对整个序列进行建模。

这表明 RNN 具有倾向于低秩、简单解的隐式偏差。除非时序数据足够强以克服正则化，否则网络将削减其自身的循环动力学。

洞察 4: 循环迫使特征学习

在深度学习理论领域，“懒惰学习 (Lazy Learning) ” (权重几乎不动，网络表现得像核机器) 和“丰富学习 (Rich Learning) ” (网络学习有用的特征) 之间存在区别。

前馈线性网络通常可能是“懒惰”的。但是循环会改变这一点吗？

作者推导了其 LRNN 的 神经正切核 (NTK) 。 NTK 描述了网络如何演变。如果 NTK 是恒定的，则学习是懒惰的。如果 NTK 发生变化，则学习是丰富的。

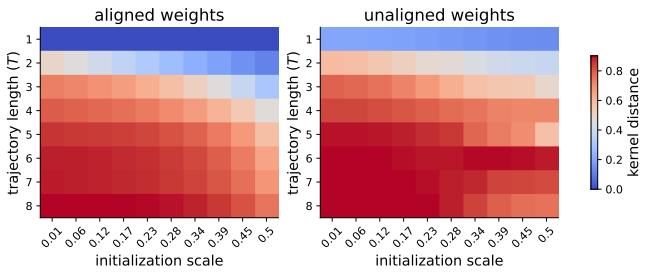
图 5: NTK 距离的热力图。较高的值表示更多的特征学习。

图 5 比较了不同轨迹长度 (\(T\)) 下 NTK 的变化 (核距离) 。

  • T=1 (底行) : 这本质上是一个前馈网络。核距离很低 (蓝色) 。
  • T=8 (顶行) : 随着序列长度的增加，核距离变为红色 (高移动) 。

这证明了 循环鼓励特征学习 。 同一个权重矩阵 \(W_h\) 的重复应用放大微小的变化，迫使网络脱离懒惰机制，并迫使其学习结构化的表示。

验证: 感官整合任务

为了证明这些理论见解不仅仅是数学上的奇思妙想，作者将它们应用于神经科学中常见的“感官整合”任务。网络接收嘈杂的输入，必须输出输入的 均值 (Mean) 或 总和 (Sum) 。

  • 求和整合: 这意味着常数动力学 (\(y = \sum x\)) 。理想的循环权重是 \(b=1\)，输入-输出权重应该是 \(1\)。这个解与 \(T\) 无关。
  • 均值整合: 这需要按 \(1/T\) 进行缩放。输入-输出权重取决于序列长度。

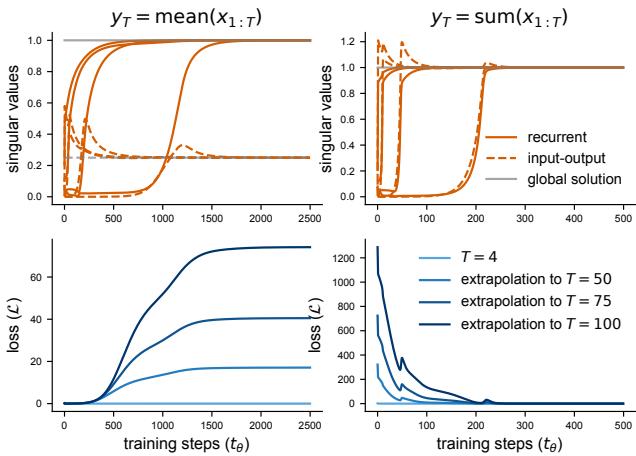
图 6: 均值与求和整合任务的实验结果，显示奇异值和损失。

图 6 中的结果证实了该理论:

  1. 顶行: 奇异值精确地收敛到理论预测的位置 (橙色线与灰色全局解重合) 。
  2. 底行:
  • 求和 (右) : 网络完美外推。即使 \(T\) 发生变化，损失仍保持在零附近。
  • 均值 (左) : 网络无法外推。因为它学习了针对训练长度的特定缩放，所以无法处理新的长度。

结论

我们经常将神经网络视为黑盒，但 Proca 等人证明我们可以打开它们——至少是线性的那些。通过将学习过程本身视为一个动态系统，他们揭示了 RNN 并不是时间的中立观察者。它们有偏见。它们更喜欢最近发生的事件。它们难以处理逐渐消逝在过去的长期依赖关系。并且它们有一种内在的压力去简化自身的连接。

这些见解有助于解释 RNN 为什么会有这样的表现，弥合了抽象的机器学习理论与生物神经科学中观察到的动力系统之间的鸿沟。随着我们迈向更复杂的架构，理解这些基本的学习动力学是构建不仅能记忆数据，而且能真正理解时间的模型的关键。