引言

聚类是机器学习和数据科学中最普遍的任务之一。无论你是为了营销活动细分客户，在社交网络中识别社区，还是将具有相似表达模式的基因分组，目标总是一样的: 对数据点进行划分，使得相似的项目在同一组，不相似的项目被分开。

谱聚类 (Spectral Clustering) 等标准技术完全依赖于数据的内在结构——即表示为相似性图的结构。但是当你拥有更多信息时会发生什么呢？在许多现实场景中，我们要掌握领域知识。我们可能确切地知道某两个特定的数据点 必须 属于同一个簇 (“必须连接”约束，Must-Link) ，或者两个点 不能 在同一个簇中 (“不能连接”约束，Cannot-Link) 。

标准的谱聚类难以自然地融合这些硬性约束。这就引出了 约束聚类问题 (Constrained Clustering Problem) 。

在这篇文章中，我们将探讨一篇研究论文，它为这个问题提出了一个数学上优雅的解决方案: CC++ 。 通过将约束建模为第二个图，并利用 符号拉普拉斯矩阵 (Signed Laplacian) 这一概念，研究人员开发了一种算法，不仅数值稳定、速度快，而且通过 Cheeger 型不等式提供了强有力的理论保证。

背景: 图与拉普拉斯矩阵

要理解这个解决方案，我们需要先确立在此语境下使用的图论词汇。

我们从一个标准的加权无向图 \(G = (V, E, w)\) 开始。这里，\(V\) 是顶点集合 (数据点) ，\(E\) 代表连接，\(w\) 函数告诉我们这些连接有多强。

标准拉普拉斯矩阵

谱聚类背后的引擎是 图拉普拉斯算子 (Graph Laplacian) 。 如果你熟悉微积分，拉普拉斯算子衡量的是梯度的散度——本质上是函数在曲面上的平滑程度。在图上，它衡量的是函数 (信号) 在顶点上的平滑程度。

标准的加权拉普拉斯算子 \(\Delta\) 作用于定义在顶点上的函数 \(\varphi\)。其定义为:

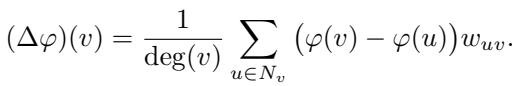
这里，\(\deg(v)\) 是顶点 \(v\) 的加权度。直观地说，这个算子将节点 \(v\) 处的函数值与其邻居的加权平均值进行比较。

映射在图上的“平滑度”可以通过与拉普拉斯矩阵相关的二次型来量化:

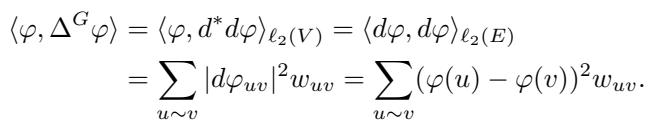
注意这一项 \((\varphi(u) - \varphi(v))^2\)。当连接的顶点 \(u\) 和 \(v\) 具有相似的值时，这个值很小。谱聚类通过最小化这个量来寻找能够分割图且不破坏强连接的切分 (cut) 。

符号拉普拉斯矩阵

论文引入了一个转折: 符号拉普拉斯矩阵 (Signed Laplacian) 。 如果边可以有负号会怎样？一个“签名 (signature) ”将边映射为 \(+1\) 或 \(-1\)。符号拉普拉斯矩阵记为 \(\Delta_{\alpha}\)，定义如下:

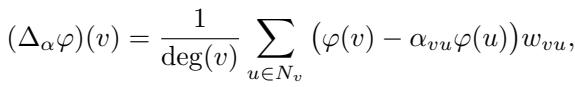
如果所有边的 \(\alpha_{vu} = 1\)，我们就得到了标准拉普拉斯矩阵。如果 \(\alpha_{vu} = -1\)，我们则得到无符号拉普拉斯矩阵 (Signless Laplacian) 。这种灵活性在后面我们需要调整约束图以确保数学计算可行时变得至关重要。

核心方法: 通过比率进行约束聚类

问题形式化

作者在同一组顶点上使用 两个 图来建模该问题:

1. 图 \(G\) : 代表数据相似性 (标准图) 。
2. 图 \(H\) : 代表约束。\(H\) 中的一条边代表一个“不能连接”约束 (或分离需求) 。

目标是找到一个顶点子集 \(S\)，使得某个特定比率最小化。我们希望切分能够切断 \(G\) 中极少的边 (保持相似性) ，但切断 \(H\) 中 许多 的边 (满足分离约束) 。

割比 (Cut Ratio) 定义为:

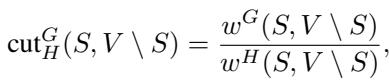
这里，\(w^G(S, V \setminus S)\) 是 \(G\) 中跨越切分的边的权重，而 \(w^H(S, V \setminus S)\) 是 \(H\) 中跨越切分的边的权重。

目标是找到使该比率最小化的集合 \(S\):

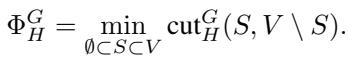
计算挑战

寻找最优离散割是一个 NP-hard 问题。然而，在谱图理论中，我们将这些离散问题松弛为连续特征值问题。

作者推导出，这个特定的比率割与一个 广义特征值问题 (Generalized Eigenvalue Problem) 相关。我们寻找满足 \(G\) 的拉普拉斯矩阵 (\(\Delta^G\)) 和 \(H\) 的拉普拉斯矩阵 (\(\Delta^H\)) 之间关系的特征值 \(\lambda\) 和特征向量 \(x\)。

具体来说，最优割受限于这两个算子的谱性质:

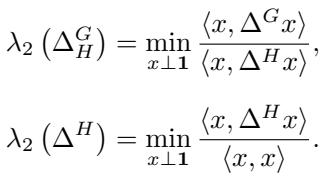
Cheeger 型不等式

该论文的主要理论贡献之一是为这种约束问题建立了一个 Cheeger 型不等式 。 在经典谱聚类中，Cheeger 不等式保证了由特征向量找到的割与真实最优割相差不会太远。

作者证明了在约束情况下也有类似的保证。如果我们对特征向量执行“扫描集 (sweep-set) ”过程 (按顶点在向量中的值排序并检查每一个可能的分割) ，得到的割 \(\Phi_H^G\) 的质量满足:

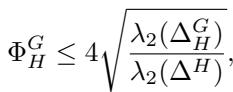
这是一个强有力的结果。它告诉我们，通过求解谱问题，我们能够保证相对于真实最优解的一定水平的性能。

CC++ 算法: 解决奇异性问题

这里有一个实际的障碍。在上面的不等式中，我们看到 \(\lambda_2(\Delta^H)\) 位于分母。如果约束图 \(H\) 是不连通的或稀疏的 (通常如此) ，它的拉普拉斯矩阵 \(\Delta^H\) 可能是奇异的 (不可逆) 或者有一个零特征值，这会导致除以零的问题。

这就是 符号拉普拉斯矩阵 大显身手的地方。

作者建议调整图 \(H\) 来创建一个新图 \(H'\)。他们在 \(H\) 中的特定顶点上添加一个 负自环 (negative self-loop) 。 等等，负环？这听起来违反直觉，但在数学上，使用符号拉普拉斯矩阵允许这样做。

通过添加一个负权重的自环并使用符号拉普拉斯矩阵 \(\Delta_{\alpha}^{H'}\)，该算子变得可逆 (正定) 。问题转化为求解以下广义特征值方程:

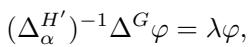
这个特定的公式是 CC++ 算法 的核心。

1. 效率: 因为 \(\Delta_{\alpha}^{H'}\) 是可逆且对称正定的，我们可以使用高效的求解器 (如 Cholesky 分解) ，而不是通用矩阵所需的较慢的 QZ 算法。
2. 稳定性: 它避免了除以接近零的数值带来的数值不稳定性。
3. 理论: 论文证明这种修改保留了足够的谱性质，使得 Cheeger 不等式仍然成立。

实验与结果

研究人员将 CC++ 与标准谱聚类 (SC) 以及未包含符号拉普拉斯改进的前一版约束聚类 (CC) 进行了对比测试。

合成数据: 随机块模型

他们使用具有两个社区的随机块模型 (SBM) 生成图。他们改变了“簇间概率” \(q\)。随着 \(q\) 的增加，两个簇混合在一起，使得它们更难区分。

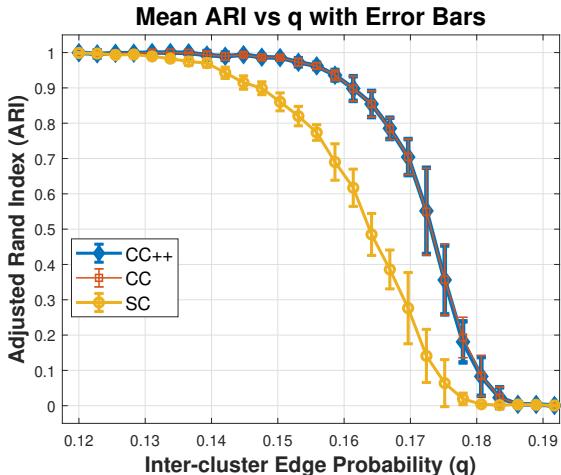
解读: 看上面的图 1。随着噪声 (\(q\)) 的增加，黄线 (SC) 迅速下降。当组别没有清晰分离时，标准谱聚类就会失效。然而，蓝线 (CC++) 即使在簇非常嘈杂 (\(q=0.18\)) 时也能保持较高的准确度 (ARI \(\approx 0.6\))，证明了约束有助于引导算法穿过噪声。

可扩展性和速度

这个方法慢吗？增加约束通常会增加复杂性。

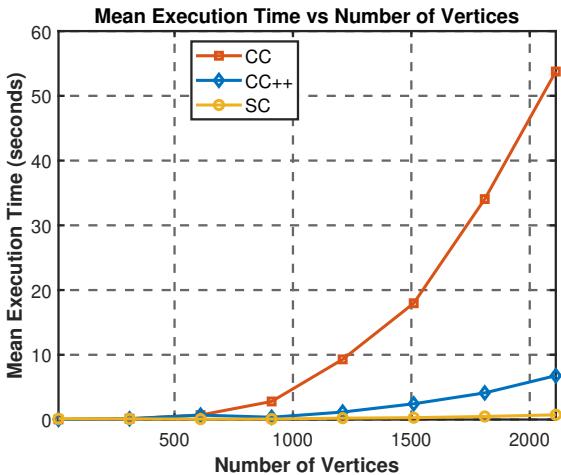
图 2 显示了执行时间。红线 (旧的 CC 方法) 随着顶点数量的增加而飙升。然而，蓝线 (CC++) 保持得非常接近黄线 (标准 SC) 。这证实了使用带有负自环的符号拉普拉斯矩阵允许使用高效的求解器，使得约束聚类具有可扩展性。

可视化差异

为了可视化算法如何处理重叠数据，他们使用了几何随机图，其中两个簇在空间上物理重叠。

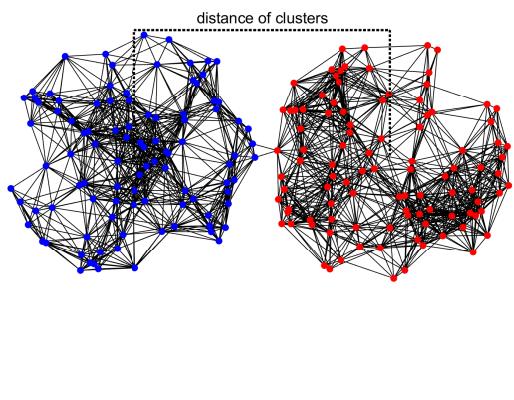
结果非常明显:

• 标准 SC 在簇重叠时完全失效 (ARI 降至 0) 。
• CC++ 保持了高准确度，因为图 \(H\) 中的“不能连接”约束告诉算法: “即使这些点在空间上很近，它们也属于不同的组。”

现实世界应用: 温度数据

作者将 CC++ 应用于法国布列塔尼的气象站数据。

• 图 G : 基于地理邻近性构建 (彼此靠近的站点相连) 。
• 图 H : 基于温度差异构建 (温度差异很大的站点在 \(H\) 中相连，代表“分离”约束) 。

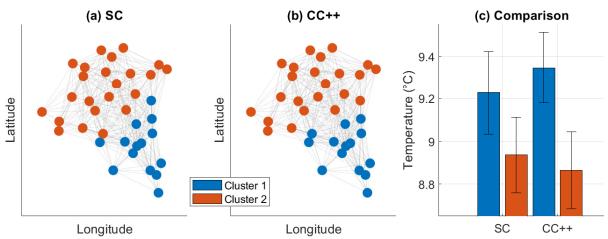
结果:

• 图 5a (SC): 仅仅基于地理位置将地图切成两半。
• 图 5b (CC++): 创建了一个更细致的聚类。它将地理上接近 且 具有相似温度特征的站点分在一组。
• 图 5c: 显示 CC++ 成功地将站点分成了不同的温度区域 (误差条没有重叠) ，而 SC 的聚类在温度上有显著重叠。

结论

这篇题为《Signed Laplacians for Constrained Graph Clustering》的研究为处理辅助信息的机器学习从业者迈出了坚实的一步。通过将约束形式化为第二个图并最小化割比，该方法既尊重数据结构又尊重用户知识。

真正的创新在于 符号拉普拉斯矩阵 。 通过巧妙地用负自环修改约束图，作者将一个计算困难且不稳定的问题转化为了一个可以像标准谱聚类一样高效求解的问题。

关键要点:

1. 约束很重要: 当数据嘈杂时，纯粹的结构聚类会失效。约束 (必须连接/不能连接) 提供了必要的护栏。
2. 比率很强大: 将问题形式化为最小化 \(G\) 中的割与 \(H\) 中的割之比，在数学上是合理的。
3. 符号拉普拉斯矩阵解决了奇异性: 引入负权重 (签名) 允许算子可逆，从而解锁了更快、更稳定的算法 (CC++)。

对于学生和从业者来说，这篇论文展示了线性代数 (特征值) 、图论 (割) 和实用算法设计之间美妙的相互作用。它提醒我们，有时一个小小的数学“技巧”——比如负环——可以带来显著的性能提升。