在机器学习的世界里，规模越大往往越好。训练庞大的模型需要海量的数据和算力，这导致了分布式学习 (Distributed Learning) 的广泛采用。我们将工作拆分给成百上千个工作节点 (如 GPU、移动设备等) ，然后由一个中央服务器聚合它们的结果来更新全局模型。

但这其中有个陷阱。在诸如联邦学习 (Federated Learning) 这样的场景中，中央服务器对工作节点的控制力很弱。有些工作节点可能会出现故障，崩溃并发送垃圾数据。更糟糕的是，有些可能是恶意的“拜占庭 (Byzantine) ”攻击者，蓄意发送在数学上精心构造的梯度来破坏模型的性能。

为了对抗这种情况，研究人员开发了拜占庭鲁棒分布式学习 (Byzantine-Robust Distributed Learning, BRDL) 。 核心思想很简单: 服务器不再信任每个工作节点，而是使用“鲁棒聚合器” (例如取中位数而不是平均值) 来过滤掉离群值。

这听起来像是一个完美的解决方案: 内置的防御系统可以保证模型的安全。但近期一篇题为*“On the Tension between Byzantine Robustness and No-Attack Accuracy in Distributed Learning”* (论分布式学习中拜占庭鲁棒性与无攻击准确性之间的张力) 的研究论文揭示了一个令人不安的真相。 这些防御措施不是免费的。

当没有攻击者存在时——这也是常态——使用这些鲁棒工具实际上会损害模型的准确性。在这篇文章中，我们将深入探讨这项研究，以理解在安全性与准确性之间存在的根本张力。

背景设定: 分布式学习与威胁

让我们从基础开始。在标准的参数服务器 (Parameter Server) 架构中，我们试图最小化全局损失函数 \(F(\mathbf{w})\)。这个函数通常是每个工作节点 \(i\) 在其本地数据上计算出的损失函数 \(F_i(\mathbf{w})\) 的平均值。

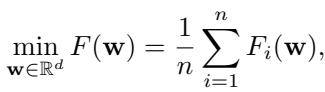
分布式学习的目标函数。

在受信任的环境中，我们使用梯度下降 (Gradient Descent, GD) 来解决这个问题。在每次迭代 \(t\) 中，服务器广播当前的模型参数。工作节点计算本地梯度 \(\mathbf{g}_i\)，服务器使用这些梯度的简单平均值来更新模型:

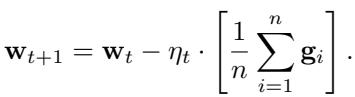
使用简单平均的标准梯度下降更新规则。

然而，简单平均极其脆弱。单个拜占庭工作节点可以发送一个任意大的梯度值 (例如无穷大) ，从而完全带偏平均值并破坏模型。

引入鲁棒聚合器

为了解决这个问题，BRDL 用鲁棒聚合器 (Robust Aggregator) (记为 \(\mathbf{Agg}\)) 替换了简单平均。

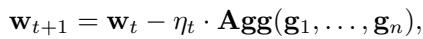
用 Agg 替换平均值的鲁棒更新规则。

这些聚合器的常见例子包括:

  • 坐标中位数 (Coordinate-wise Median) : 取每个参数的中位数值。
  • 截尾均值 (Trimmed Mean) : 在平均之前去除最大和最小的值。
  • Krum / 几何中位数 (Geometric Median) : 基于空间几何选择更新。

这些方法旨在容忍总共 \(n\) 个工作节点中最多 \(f\) 个恶意工作节点。在数学上，现有文献将一个聚合器定义为 \((f, \kappa)\)-鲁棒 , 如果它满足特定的不等式:

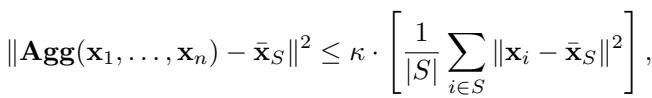
(f, kappa)-鲁棒性的定义。

本质上，这个定义确保了聚合结果接近诚实工作节点的“真实”均值 (\(\bar{\mathbf{x}}_S\)) ，且受常数 \(\kappa\) 的限制。

核心问题: 鲁棒性的代价

论文提出了一个关键问题: 如果我们开启了这些防御措施，但并没有人攻击我们，会发生什么?

在没有拜占庭工作节点的场景中，“真实”的更新应该是所有工作节点的平均值 (\(\bar{\mathbf{x}}\)) 。然而，鲁棒聚合器被设计用来忽略或降低离群值的权重。在分布式学习中，“离群值”并不总是坏的——它们可能只是拥有独特、多样化数据分布 (异构数据) 的诚实工作节点。

如果一个鲁棒聚合器仅仅因为某些有效梯度看起来“与众不同”就将其丢弃，这就会引入聚合误差 。

为了量化这一点，作者引入了一个新的指标，称为 \(\epsilon\)-准确性 (\(\epsilon\)-accuracy) 。 它衡量了当所有人都是诚实的时候，聚合器偏离真实均值的程度。

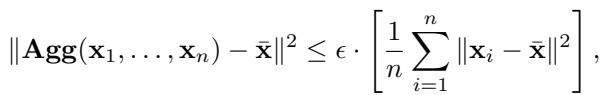
epsilon-准确性的定义。

在这里，\(\epsilon\) 代表了聚合器的“代价”。一个完美的聚合器 (如简单均值) 在没有攻击的情况下 \(\epsilon = 0\)。但正如我们将看到的，鲁棒聚合器通常 \(\epsilon > 0\)。

通用下界

作者证明了一个重要的理论结果: 没有高误差就无法获得高鲁棒性。

如果你希望聚合器能容忍 \(f\) 个拜占庭工作节点，它必须具有与该容忍度成正比的最坏情况误差。具体来说，论文证明对于任何鲁棒聚合器:

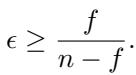
epsilon 的下界。

这是一个深刻的发现。分数 \(\frac{f}{n-f}\) 随着 \(f\) 的增加而增加。

  • 如果你假设有 0 个攻击者 (\(f=0\)) ，误差下界为 0。
  • 如果你想容忍接近一半的网络是恶意的 (\(f \approx n/2\)) ，误差的下界将飙升至接近 1 (这意味着误差与数据本身的方差一样大) 。

这个不等式在数学上形式化了标题中提到的“张力”。为了防备更多的敌人 (\(f\)) ，你不可避免地会降低没有敌人出现时的性能。

分析特定的聚合器

研究人员不仅止步于通用界限；他们分析了三种特定的、流行的聚合器，看看它们相对于这个理论的表现如何。

1. 坐标截尾均值 (\(TM_{f/n}\))

截尾均值的工作原理是去除每个坐标上最大的 \(f\) 个和最小的 \(f\) 个值，然后对其余的进行平均。

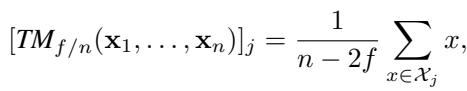
坐标截尾均值的定义。

直觉上，如果数据是偏斜的，忽略分布的尾部会引入误差。作者证明，对于截尾均值，准确性参数 \(\epsilon\) 恰好是:

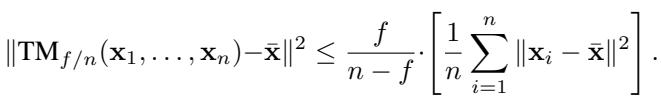
截尾均值的 epsilon 值。

注意，这完美契合了通用下界 。 这意味着截尾均值在某种意义上是鲁棒性最优的——但它仍然受制于由 \(f/(n-f)\) 定义的不可避免的误差基底。

2. 坐标中位数 (CM)

中位数是截尾均值的极端版本 (截去了几乎所有值) 。

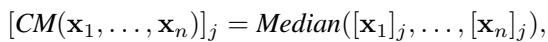
坐标中位数的定义。

分析表明，中位数具有高得多的 \(\epsilon\)。虽然鲁棒，但它丢弃了太多来自诚实工作节点的信息，以至于它在无攻击场景下的误差非常高。

3. 几何中位数 (GM)

几何中位数寻找一个向量，使其到所有输入向量的欧几里得距离之和最小。

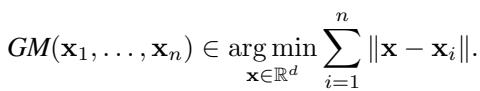
几何中位数的定义。

论文证明几何中位数是 1-准确的 (\(\epsilon = 1\)) 。与截尾均值 (当 \(f\) 较小时) 相比，这相当高，表明在良性设置下有巨大的信息损失。

误差界限总结

下表总结了这些发现。我们可以看到 \(\epsilon\) (无攻击误差) 与 \(\kappa\) (鲁棒性常数) 是截然不同的。

表 2 总结了不同聚合器的 epsilon 值。

误差何时最严重？

理论提供了一个“最坏情况”的界限。但最坏情况长什么样呢？

通过证明，作者确定了最大化聚合误差的条件。对于截尾均值，当数据分布高度偏斜时误差最大。具体来说，如果 \(f\) 个工作节点聚集在一个极端，而其余 \(n-f\) 个工作节点聚集在另一个极端:

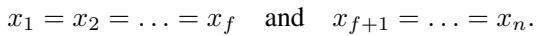
最坏情况下的数据分布条件。

这揭示了与数据异构性 (Data Heterogeneity) 的联系。在分布式学习中，如果所有工作节点拥有相同的数据 (独立同分布，IID) ，它们的梯度将是相同的，鲁棒聚合器将输出与均值相同的值。然而，在现实场景 (非独立同分布，Non-IID) 中，工作节点拥有不同的数据。这造成了梯度的偏斜。

关键结论: 当数据是异构的时，鲁棒性与准确性之间的张力被放大了。数据越多样化，存在的“诚实离群点”就越多，鲁棒聚合器错误地抑制它们的情况就越严重。

对收敛性的影响

我们知道鲁棒聚合器在单步更新中引入了误差。但这会破坏成千上万步的整个训练过程吗？

作者分析了拜占庭鲁棒梯度下降 (ByzGD) 的收敛性。他们依赖于该领域的标准假设:

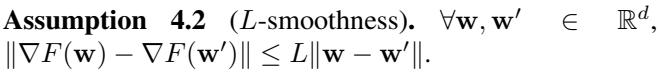
  1. L-平滑性 (L-Smoothness) : 损失函数的变化不会太剧烈。 L-平滑性假设。
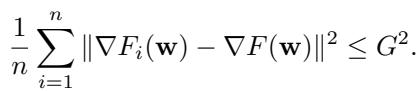
  2. 有界异构性 (Bounded Heterogeneity) : 工作节点间梯度的差异被限制在 \(G^2\) 以内。 有界异构性假设。

收敛下界

主要的收敛定理 (定理 4.5) 是悲观的。它指出，即使经过完美调整，梯度范数 (衡量我们离解有多近的指标) 也无法收敛到零。它会被卡在某个基底 \(C_1\) 之上:

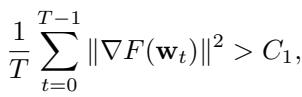
梯度范数收敛的下界。

同样，损失函数值将保持在最优值 \(F^*\) 之上:

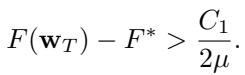
函数值收敛的下界。

关键在于，这个误差基底 \(C_1\) 与 \(\frac{f}{n-f} G^2\) 成正比。

这证实了早先的直觉:

  • 更高的 \(f\) (更高的鲁棒性) \(\rightarrow\) 更高的误差基底。
  • 更高的 \(G\) (更高的异构性) \(\rightarrow\) 更高的误差基底。

上界

为了确保这个下界不仅仅是一个宽松的理论估计，作者还为满足 PL-条件的凸函数证明了一个上界 (定理 4.6) 。

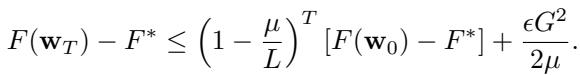
上界收敛率。

随着时间 \(T \to \infty\)，第一项消失，但第二项 \(\frac{\epsilon G^2}{2\mu}\) 依然存在。由于我们知道 \(\epsilon \geq \frac{f}{n-f}\)，上界和下界讲述了同一个故事: 如果在异构环境中使用鲁棒聚合器，你无法实现完美优化。

实验证据

为了支持数学推导，研究人员在 CIFAR-10 数据集上训练了一个 ResNet-20 模型。他们在没有任何攻击的情况下测试模型，以衡量鲁棒性的纯粹代价。

他们使用狄利克雷分布参数 \(\alpha\) 来控制数据异构性。

  • 低 \(\alpha\) (例如 0.1) : 高度异构 (Non-IID) 。
  • 高 \(\alpha\) (例如 10.0) : 较为均匀 (IID) 。

结果: 增加鲁棒性 (\(f\)) 会损害准确率

实验测试了 “Multi-Krum” 和 “坐标截尾均值”。

在 Multi-Krum 的结果中 (显示在论文的表 3 中，此处未展示但已描述) ，当 \(f=0\) (标准均值) 时，准确率约为 89%。当他们将容忍度 \(f\) 增加到 7 时，在异构情况下 (\(\alpha=0.1\)) ，准确率暴跌至约 40%。

截尾均值的结果 (论文中的表 4) 显示了类似的趋势。在高异构性 (\(\alpha=0.1\)) 下，将 \(f\) 从 0 增加到 7 导致准确率从大约 89% 降至 10%。

这验证了理论: 如果数据是多样化的，简单地开启“防御”旋钮 (\(f\)) 会破坏模型，即使没有任何攻击者存在。

混合 (Mixing) 有帮助吗？

最近邻混合 (Nearest Neighbor Mixing, NNM) 是一种常被提出来减少异构性的技术。它在聚合之前混合工作节点之间的梯度，使它们更加相似。

作者测试了这是否有帮助。

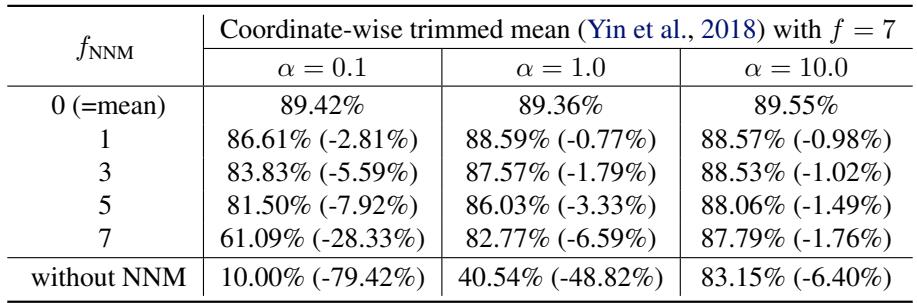
表 6: 带 NNM 的截尾均值。

在上表 (带 NNM 的坐标截尾均值) 中，查看 \(\alpha=0.1\) (高异构性) 这一列。

  • 不使用 NNM，准确率实际上崩溃了 (10.00%) 。
  • 使用 NNM，准确率显著恢复 (在 \(f_{NNM}=1\) 时高达约 86%) 。

然而，张力依然存在。使用较小的 \(f_{NNM}\) 虽然提高了准确率，但也降低了系统的有效鲁棒性。即使有了缓解策略，这种权衡仍然存在。

结论与启示

这项研究充当了拜占庭鲁棒分布式学习领域的现实检验。

  1. 天下没有免费的午餐: 你不能在最大化对攻击者的防御 (\(f\)) 的同时，不降低模型对诚实用户的性能 (\(\epsilon\)) 。
  2. 异构性是敌人: 当各工作节点数据相同时，这种权衡可以忽略不计，但在现实世界的 Non-IID 场景 (如联邦学习) 中，这种权衡变得非常严峻。
  3. 参数估计至关重要: 在实践中，工程师必须仔细估计实际可能存在的攻击者数量。为了“以防万一”而将 \(f\) 设置为理论最大值，很可能会使模型在良性环境中变得毫无用处。

随着分布式系统成为训练 AI 的标准，理解这种“偏执的代价”对于构建既安全又有效的系统至关重要。