引言

聚类是数据分析中最直观的任务之一。我们看着一堆数据点——无论是图像、文档还是生物样本——并试图将相似的项目归为一组，同时将不相似的项目分开。但是，当仅凭“相似性”还不够时会发生什么？

想象一下，你正在对新闻文章进行聚类。算法可能会因为两篇文章共享关键字而将它们归为一组。然而，作为人类专家，你知道其中一篇文章是关于 2024 年奥运会的，而另一篇是关于 2028 年奥运会的。你想强制执行一条硬性规则: 这两篇文章必须严格处于不同的簇中。反之，你可能有两篇不同语言的文章描述的是完全相同的事件；你想强制要求它们最终处于同一个簇中。

这就是受限相关聚类 (Constrained Correlation Clustering, CCC) 的领域。它采用了标准的聚类问题，并添加了“必须连接 (Must-Link)”和“不能连接 (Cannot-Link)”的约束。虽然这听起来像是一个微小的调整，但它使数学问题变得更加困难。多年来，针对该问题的最佳理论算法提供了一个“3-近似 (3-approximation)”——这意味着找到的解决方案的成本可能是完美、最优解决方案的三倍。

在标准 (无受限) 相关聚类中，研究人员早已打破了“2-近似”的壁垒，取得了更紧密的结果。但受限版本一直停留在 3。直到现在。

在论文 “Towards Better-than-2 Approximation for Constrained Correlation Clustering” 中，研究人员 Andreas Kalavas、Evangelos Kipouridis 和 Nithin Varma 提出了一种突破性的方法。通过将线性规划 (LP) 与巧妙的“局部搜索 (Local Search)”技术相结合，他们表明——以能够有效求解 LP 为条件——我们可以实现 1.92 的近似因子。

在这篇文章中，我们将剖析这篇复杂的论文。我们将探索他们如何使用分数解来指导离散搜索，如何“混合”不同的聚类以避免最坏情况，以及他们最终如何突破 2 的壁垒。

背景: 游戏规则

在深入研究新方法之前，让我们先建立相关聚类的基本规则，以及为什么约束会使事情变得复杂。

相关聚类 (Correlation Clustering)

在该问题的标准版本中，给定一个完全图，其中每对节点 (顶点) 都有一条标记为 \(+\) (加号/正) 或 \(-\) (减号/负) 的边。

  • 正边 (+): 这些节点希望在同一个簇中。
  • 负边 (-): 这些节点希望在不同的簇中。

目标是将节点划分为若干个簇，以最小化成本 (Cost) , 成本由以下两部分组成:

  1. 簇内的负边 (彼此讨厌但被迫在一起的项目) 。
  2. 簇间的正边 (彼此喜欢但被分开的项目) 。

相关聚类的一个关键特征是你不需要预先指定簇的数量 (\(k\))。算法会根据边标签自然地决定最优的 \(k\)。

添加约束

受限版本引入了两组硬性约束:

  • 友好对 (\(F\)): 一组必须在同一个簇中的节点对。
  • 敌对对 (\(H\)): 一组必须在不同簇中的节点对。

你可能会想，“我们不能直接将友好对合并成超节点，然后照常进行吗？”不幸的是，不能。合并节点会产生加权边和结构依赖性，标准算法在处理这些问题时会失去其近似保证。此外，一个有效的聚类必须满足 \(F\) 和 \(H\) 中的所有约束。如果你有一个友好对 \((u, v)\) 和一个敌对对 \((u, w)\)，那么 \((v, w)\) 隐式地也就变成了敌对关系。管理这些传递关系非常棘手。

度量标准: 近似因子

由于找到精确的最优聚类是 NP-难的 (对于大数据集在计算上是不可能的) ，我们寻找近似算法。如果一个算法满足以下条件，则称其为 \(\alpha\)-近似:

\[ \text{Cost(Our Algorithm)} \le \alpha \times \text{Cost(Optimal Solution)} \]

对于 CCC，之前最好的 \(\alpha\) 是 3。这篇论文的目标是 \(\alpha < 2\)。

核心方法

作者的方法是混合算法设计的典范。它不仅仅依赖于一种技术。相反，它结合了线性规划 (Linear Programming, LP) 来获得世界的“分数”视图，以及局部搜索 (Local Search) 将该分数转化为可靠的、离散的聚类。

这是他们算法的高级路线图:

  1. LP: 求解一个巨大的线性规划以获得“分数最优”解。
  2. 局部搜索 1: 使用 LP 指导搜索以获得一个好的聚类 (\(\mathcal{L}\))。
  3. 局部搜索 2: 如果 \(\mathcal{L}\) 不够好，运行第二次搜索 (\(\mathcal{L}'\))，该搜索会因与 \(\mathcal{L}\) 相似而受到惩罚。
  4. 枢轴 (混合): 如果两次搜索都未能打破壁垒，则将它们与 LP 解结合起来形成第三个聚类 (\(\mathcal{P}\))，该聚类被保证是优秀的。

让我们逐步分解这些步骤。

1. 受限聚类 LP (The Constrained Cluster LP)

这种方法的基础是线性规划 (LP)。用于聚类的标准 LP 通常分配一个介于 0 和 1 之间的变量 \(x_{uv}\)，表示两个节点之间的“距离” (0 = 同一簇，1 = 不同簇) 。

然而，作者使用了一种更强大的公式，称为聚类 LP (Cluster LP) 。 他们不仅仅关注点对，而是关注潜在的簇。

设 \(z_C\) 为一个变量，表示特定节点集合 \(C\) 形成一个簇的概率。 设 \(x_{uv}\) 为节点 \(u\) 和 \(v\) 之间的导出距离。

LP 试图最小化分歧的成本:

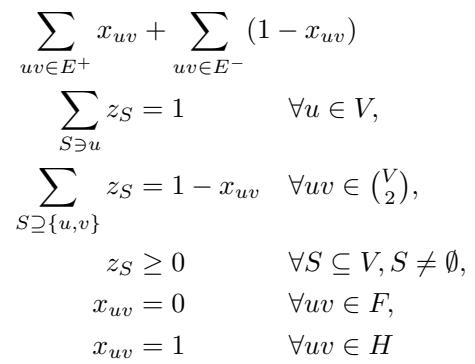
受限聚类 LP 公式，显示目标函数和约束条件。

让我们解读上面的图 1:

  • 目标: 最小化正边的距离 (\(x_{uv}\)) 和负边的相似度 (\(1-x_{uv}\)) 之和。这是聚类成本的分数模拟。
  • 约束 1 (\(\sum z_S = 1\)): 每个节点 \(u\) 必须恰好属于一个簇分布 (包含 \(u\) 的簇的概率之和为 1) 。
  • 约束 2 (\(1 - x_{uv}\)): \(u\) 和 \(v\) 在同一个簇中的概率等于包含两者的所有簇 \(S\) 的 \(z_S\) 之和。
  • 硬约束: 最后两行至关重要。如果一对节点在 \(F\) (友好) 中，它们的距离 \(x_{uv}\) 被强制为 0。如果在 \(H\) (敌对) 中，则被强制为 1。

假设: 作者假设我们可以有效地求解这个 LP。虽然潜在簇 \(C\) 的数量是指数级的，但对于无受限聚类，我们知道如何在多项式时间内求解。作者假设这也可能适用于受限版本，或者我们可以得到足够接近的解。论文的其余部分假设我们拥有这个解。

2. 局部搜索: 第一轮

现在我们有了一个分数解 (一系列权重 \(z_C > 0\) 的簇 \(C\)) ，我们需要一个实际的聚类。作者使用局部搜索策略。

局部搜索如何工作

  1. 从任何满足硬约束的有效聚类开始。
  2. 查看 LP 识别出的“好”簇 (那些 \(z_C > 0\) 的簇) 。
  3. 从 LP 解中选择一个簇 \(C\)。
  4. 移动: 检查将 \(C\) 强制放入当前聚类是否会改善总成本。如果你添加 \(C\)，你会从旧簇中移除 \(C\) 中的节点并将它们组合在一起。旧簇的剩余片段保持原样。
  5. 重复此过程，直到没有更多的单簇交换能改善成本为止。

让我们称得到的聚类为 \(\mathcal{L}\)。

作者证明了这个简单过程的一个强有力的界限。他们表明 \(\mathcal{L}\) 的成本与 LP 解的成本 (\(\text{LP}\)) 之间存在如下不等式关系:

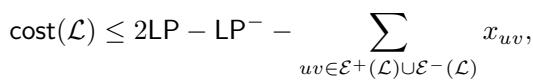
不等式显示 L 的成本小于或等于 2LP 减去 LP-minus 减去未满足边的 x_uv 之和。

让我们分析上面的图片。它指出我们的聚类 \(\mathcal{L}\) 的成本最多是 \(2 \times \text{LP}\) 。 这立即给了我们一个 2-近似！

但仔细看看负项。成本实际上比 \(2 \text{LP}\) 更优，优化的量为:

  1. \(\text{LP}^-\) (LP 针对负边的成本)。
  2. 我们的聚类 \(\mathcal{L}\) 未能满足的边的距离 \(x_{uv}\)。

这意味着 \(\mathcal{L}\) 严格优于 2-近似，除非这些减去的项非常小。如果 \(\mathcal{L}\) 是“坏的” (即接近因子 2) ，这意味着必须满足关于哪些边被满足的特定条件。

具体来说，如果 \(\mathcal{L}\) 不够好，这意味着 LP 为负边支付的成本不多，而且我们切断的正边在 LP 中的距离 \(x_{uv}\) 非常小。

3. 带惩罚的局部搜索

作者定义了一个小常数 \(\delta\) (delta)。他们的目标是证明可以实现 \((2-\delta)\)-近似。

从上一节可知，如果 \(\mathcal{L}\) 未能成为 \((2-\delta)\)-近似，我们知道“误差”是以特定方式集中的。为了对此进行反击，作者再次运行局部搜索以生成第二个聚类 \(\mathcal{L}'\)。

但我们不希望 \(\mathcal{L}'\) 犯与 \(\mathcal{L}\) 相同的错误。我们希望它是不同的。因此，他们修改了第二次搜索的成本函数。他们添加了一个惩罚 :

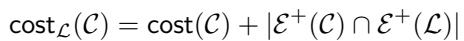
定义惩罚成本函数 cost_L(C) 的方程。

如上图所示，新的成本函数 \(\text{cost}_\mathcal{L}(\mathcal{C})\) 是正常成本加上在新聚类和旧聚类 \(\mathcal{L}\) 中都未被满足的正边数量。

直观地说，这迫使算法: “找到一个低成本的聚类，但要非常努力地满足第一个聚类未能满足的那些正边。”

如果第二个聚类 \(\mathcal{L}'\) 也不优于 2-近似，这意味着对 LP 解有更严格的条件。我们现在有两个“失败”的聚类，但它们的失败为我们提供了关于问题实例的结构信息。

4. 枢轴操作: 混合一切

这是论文中最具创新性的部分。我们有三种成分:

  1. \(\mathcal{L}\): 第一次局部搜索的结果。
  2. \(\mathcal{L}'\): 带惩罚的局部搜索的结果。
  3. \(\mathcal{I}\): 通过随机舍入 LP 解生成的聚类 (一个称为“采样”的过程) 。

如果 \(\mathcal{L}\) 和 \(\mathcal{L}'\) 都“坏” (接近 2-近似) ，作者通过混合这三个聚类来构造一个新的聚类 \(\mathcal{P}\)。

标签系统

为了构建 \(\mathcal{P}\)，他们为每个节点 \(u\) 分配一个由三个坐标 \((X, Y, Z)\) 组成的标签:

  • \(X\): 聚类 \(\mathcal{L}\) 中包含 \(u\) 的簇。
  • \(Y\): 聚类 \(\mathcal{L}'\) 中包含 \(u\) 的簇。
  • \(Z\): 聚类 \(\mathcal{I}\) 中包含 \(u\) 的簇。

然后算法根据这些标签对节点进行分组。

  • 具有完全相同标签 \((X, Y, Z)\) 的节点形成新簇的核心。
  • 仅在一个坐标上不同的节点被吸收到这些核心中。

为什么这行得通？作者定义了一个“枢轴过程 (Pivoting Procedure)” (论文中的算法 4) 。其逻辑依赖于假设 \(\mathcal{L}\) 和 \(\mathcal{L}'\) 是坏的。如果它们是坏的，它们肯定未能满足不同的边集 (因为有惩罚) 。通过将它们与 LP 舍入解 \(\mathcal{I}\) 相结合，新聚类 \(\mathcal{P}\) 捕获了其他聚类错过的边。

实验与结果: 理论证明

在理论计算机科学论文中，“结果”通常指的是数学证明，而不是数据集上的基准测试。作者通过反证法提供了严格的证明。

逻辑: 假设 \(\mathcal{L}\) 和 \(\mathcal{L}'\) 均未达到 \((2-\delta)\) 近似。

步骤 1: 分析“坏”的 \(\mathcal{L}\) 如果 \(\mathcal{L}\) 是坏的，LP 成本必须满足某些界限。具体来说，LP 中的“负”边成本必须很小，而被 \(\mathcal{L}\) 切断的“正”边必须具有较低的 LP 权重。

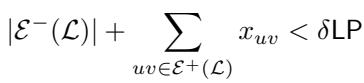
不等式表明如果 L 不是最优的，坏边的总和小于 delta 乘以 LP。

步骤 2: 分析“坏”的 \(\mathcal{L}'\) 如果 \(\mathcal{L}'\) 也是坏的，我们会得到一个类似的不等式，但它包含了与 \(\mathcal{L}\) 的误差交集。

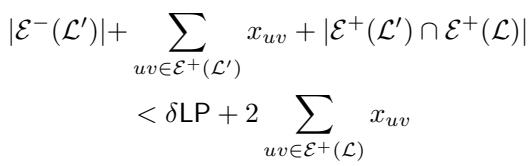
L-prime 的不等式显示了涉及与 L 交集的成本界限。

步骤 3: 组合界限 将这些条件加在一起告诉我们，导致问题的边的总权重相对于 LP 成本其实相当小。

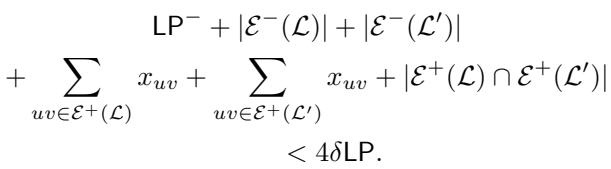
组合不等式显示误差总和小于 4 delta LP。

这张图本质上是在说: “如果两次局部搜索都失败了，所有解决方案中所有‘有问题’的边的总权重小于 \(4\delta \text{LP}\)。”

步骤 4: \(\mathcal{P}\) 的构造 作者验证了第三个聚类 \(\mathcal{P}\) 的成本。

  • 如果 \(\mathcal{P}\) 为一条负边付费，这意味着端点在标签坐标中最多有两个不同 (因此 \(\mathcal{L}\)、\(\mathcal{L}'\) 或 \(\mathcal{I}\) 已经为此付费了) 。
  • 如果 \(\mathcal{P}\) 为一条正边付费，则端点至少有两个坐标不同。

由于 \(\mathcal{L}\)、\(\mathcal{L}'\) 和 \(\mathcal{I}\) 的总“糟糕程度”是有界的 (如步骤 3 所示) ，\(\mathcal{P}\) 的成本也必须很低。

结论: 数学推导表明，如果我们设定 \(\delta \approx 0.08\)，那么在 \(\mathcal{L}\) 和 \(\mathcal{L}'\) 失败的最坏情况下，\(\mathcal{P}\) 会成功。

具体来说，作者证明了该算法总是返回一个成本最多为 \((1.92 + \varepsilon) \text{LP}\) 的解。

结论与意义

近二十年来，受限相关聚类一直停留在 3-近似。这篇论文代表了一次重大飞跃，将近似因子降低到了 1.92 。

关键要点:

  1. 约束改变了游戏规则: 你不能简单地“合并并运行”标准算法。约束需要处理几何依赖关系。
  2. LP 是强有力的向导: 即使我们不能直接使用分数 LP 解，它也可以作为地图。它告诉我们哪些簇是“自然”的候选者。
  3. 冗余有帮助: 运行算法两次——一次正常运行，一次带有强制多样性的惩罚——暴露了问题实例的结构弱点。
  4. 混合解决方案: 基于节点标签进行“枢轴”操作或混合多个聚类的想法是利用不完美方案构建高质量解的强大技术。

潜在问题: 该结果依赖于受限聚类 LP 可以被有效地求解 (或近似) 这一假设。虽然这对于无受限版本是成立的，并且作者提供了强有力的论据说明为什么这里也应该成立，但这仍然是实现完全多项式时间实现的最后障碍。

尽管如此，这项工作为打破 2 的壁垒提供了理论蓝图。它弥合了受限数据的混乱现实与近似算法的优雅世界之间的鸿沟。对于机器学习的学生和研究人员来说，它强调了有时为了解决一个离散问题，你必须从分数的角度看它，然后局部地看，最后将所有内容混合在一起。