在机器学习中，优化就是一切。无论你是在训练语言模型、为自动驾驶汽车微调视觉网络，还是拟合一个简单的逻辑回归，你总是在使用优化器——一个推动模型参数迈向更好性能的数学引擎。

几十年来，这一领域一直依赖精心手工设计的优化器，如 SGD、ADAM 和 RMSProp 。 这些“老黄牛”通过高效地训练大型网络，彻底改变了深度学习的发展。

但如果优化过程本身也能被学习呢？我们能否不再手动设计更新规则，而是训练一个神经网络去成为优化器——让它自己发现探索损失函数景观的策略？这个理念通常被称为 学习如何学习 (learning to learn) 或 元学习 (meta-learning) , 是当代人工智能研究中最激动人心的方向之一。

早期的尝试虽有潜力，但存在明显的限制。学习型优化器在其训练的特定问题上表现良好，但无法泛化。它们十分脆弱，难以应对新的模型架构或未见过的数据分布。更糟糕的是，它们无法扩展: 为每个参数运行一个独立神经网络的计算成本很快就变得极其高昂。

在来自 Google Brain 和 DeepMind 的开创性论文 《Learned Optimizers that Scale and Generalize》 中，研究员 Olga Wichrowska 及其同事正面解决了这些挑战。他们提出了一种学习型优化器，不仅能泛化到全新的任务，还能扩展到训练真实世界的模型，例如在 ImageNet 上的 InceptionV3 和 ResNetV2——这些模型规模比训练阶段见过的任何模型都大多个数量级。

这篇博文将拆解他们是如何实现这一突破的——从架构创新到巧妙的训练策略，这些都赋予了优化器前所未有的灵活性和鲁棒性。

早期学习型优化器的局限

Andrychowicz 等人 (2016) 的早期工作提出了基于 RNN 的学习型优化器，它直接学习如何执行梯度下降。在每一步迭代中，RNN 接收参数的梯度并产生更新。

虽然这一思路很优雅，但它有两个致命缺陷:

  1. 泛化能力差: 在一类狭窄问题上训练的优化器——例如使用 sigmoid 激活函数的小型网络——在面对稍有不同的结构 (如 ReLU 网络) 时往往完全失效。
  2. 计算开销巨大: 为每个参数运行一个 RNN 会产生极高的计算和内存成本，大型模型几乎无法这样进行优化。

Wichrowska 等人的工作用一种新的分层设计解决了以上两大问题，该设计能自然地扩展，并学到可以在不同问题类型间迁移的行为。

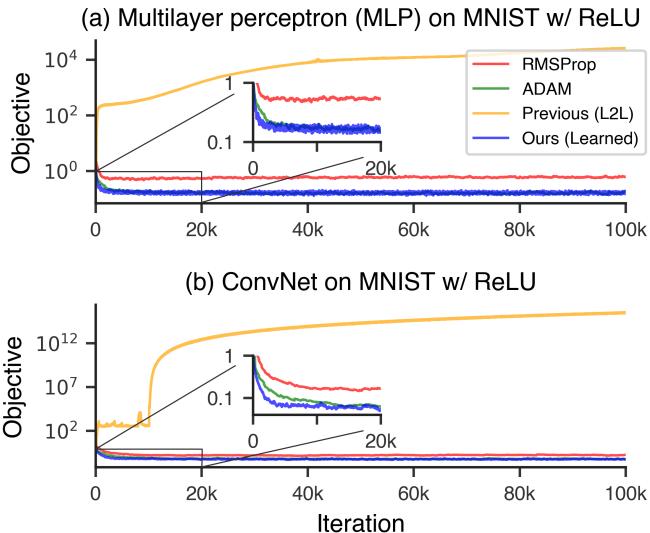
先前学习型优化器 (L2L) 与新优化器 (Ours) 的训练损失对比。前者在 ReLU 激活的网络上发散，而新优化器保持稳定，并与 ADAM 和 RMSProp 具有竞争力。

图 2. 先前的学习型优化器在未见过的架构上失效，而本文提出的分层优化器保持稳定且高效。

更智能的神经架构

该论文的核心是一个分层循环架构 (hierarchical recurrent architecture) ——一个三层 RNN，反映了神经网络参数的自然层次结构。

分层设计

与将每个参数视为独立实体的做法不同，该优化器围绕张量 (如权重矩阵和偏置向量) 及网络层组织自身。这极大地减少了开销，同时保留了对相关参数进行联合推理的能力。

整个结构包含三个层次:

  1. 参数 RNN (底层) : 每个标量参数运行一个微型 RNN，仅含 5–10 个隐藏单元，用于局部更新。
  2. 张量 RNN (中层) : 每个参数张量 (例如一层的所有权重) 都有自己的 RNN。它聚合其子参数 RNN 的隐藏状态，并向它们发送偏置信号以协调更新。
  3. 全局 RNN (顶层) : 单个全局 RNN 处理来自所有张量级单元的信号，统一整个网络的信息，使层间通信成为可能，并捕捉全局趋势。

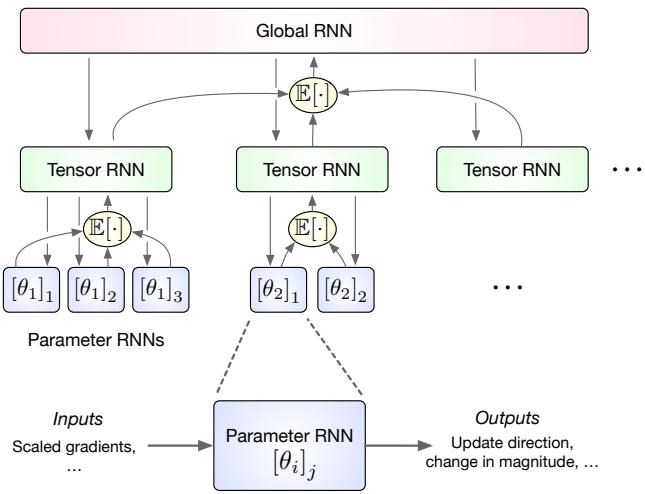
分层 RNN 架构由一个全局 RNN、多个张量 RNN (每个参数组一个) 和许多小型参数 RNN (每个标量参数一个) 组成。

图 1. 分层架构能以最小开销实现跨参数的协调。

这种层次结构使优化器极具可扩展性。尽管每个参数只有一个微小的局部 RNN，但整个优化器能够在张量与层级之间传递结构感知的更新，捕获类似二阶优化行为的相互作用——而不会导致模型规模爆炸。

内建优化智慧

作者没有让网络从头自行摸索几十年的优化经验，而是将经典优化方法中的有效归纳偏置融入架构中。下面四个功能尤为突出:

1. 前瞻计算: 注意力与动量结合

受 Nesterov 动量 和 注意力机制 启发，优化器有时不在当前参数值处计算梯度，而是在一个前瞻位置:

\[ \phi_t^{n+1} = \theta_t^n + \Delta \phi_t^n \]

这种偏移使网络能“预览”损失景观的前方，帮助预测曲率，进而更稳健地朝最小值方向移动。

2. 多时间尺度的动量

传统动量只使用单一指数移动平均来平滑梯度。而该学习型优化器在多个时间尺度上跟踪移动平均——从快速的短期估计到缓慢的长期趋势。

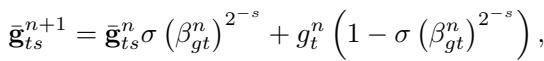
在不同时间尺度上更新梯度移动平均的公式。

比较多个窗口内的梯度平均值，为优化器提供关于曲率和噪声的信息，从而提高稳定性和适应性。

通过比较这些不同时间尺度的平均值，RNN 能估计梯度的噪声水平和损失表面的变化趋势——这些都是动态调整步长的关键依据。

3. 动态输入缩放

借鉴 RMSProp 和 ADAM 的思想，该优化器在将梯度输入 RNN 之前先进行缩放。这确保了无论参数尺度如何，都能保持稳定的行为。

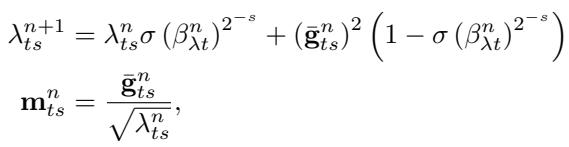
计算梯度平方的移动平均 (λ) 和缩放后的梯度 (m) 的公式，它们作为 RNN 的输入。

动态输入缩放可保持梯度的良好数值条件，提高训练稳定性。

此外，它还计算参数间的相对梯度大小，帮助网络理解模型不同部分的演化方式。

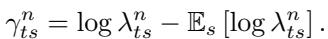
相对对数梯度大小的公式，它帮助优化器比较不同时间尺度上的梯度尺度。

相对缩放使优化器能够比较梯度在不同层和时间尺度上的变化。

4. 分离步长与方向

经典自适应优化器会将前进方向与步长大小分离。该学习型优化器采用了相同的思想:

\[ \Delta \theta_t^n = \exp(\eta_{\theta t}^n) \frac{\mathbf{d}_{\theta t}^n}{||\mathbf{d}_{\theta t}^n|| / N_t} \]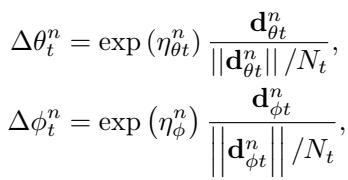

参数更新被分解为步长 (exp(η)) 与归一化方向向量。

优化器将方向与步幅大小解耦，提高了对参数缩放的鲁棒性。

关键在于，RNN 不直接输出学习率的绝对值，而是预测学习率的变化量 。 这迫使它在不同任务和时间尺度上动态适应。

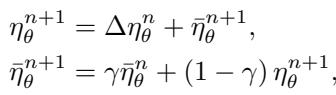
对数学习率 (η) 相对于其指数移动平均更新；RNN 输出变化量而非绝对值。

学习率随时间变化，使优化器能在多样任务中实现有效泛化。

元训练: 教优化器学会学习

一个优秀的架构同样需要精心设计的训练过程。研究人员没有用大规模神经网络作为训练对象，而是构建了一组紧凑但多样的合成优化问题，以捕捉真实世界挑战的核心特征。

多样化的训练集

元训练集包括:

  • 经典病态函数 : 如 Rosenbrock、Ackley 和 Beale——这些函数具有陡峭峡谷与迷惑性最小值。
  • 凸优化问题 : 如二次碗型函数和逻辑回归任务。
  • 带噪声的梯度问题 : 包括小批量损失与随机噪声注入。
  • 慢收敛任务 : 梯度稀疏或振荡的情况。
  • 变换后的问题 : 包含变量缩放、幂律扭曲或多任务混合等。

训练中未涉及任何神经网络。这种多样性迫使优化器学习损失表面的普遍特征，而非记忆某类网络的特殊模式。

元目标: 聚焦精确收敛

作者没有最小化平均损失，而是最小化每一步损失的对数值 。

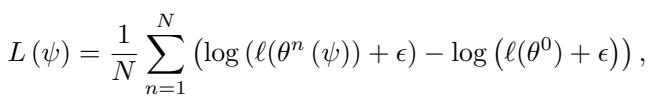
元目标是训练轨迹上对数损失的平均值。

对数损失目标奖励那些能将函数值精确逼近零的优化器，从而促进高精度收敛。

这一微妙的设计让优化器倾向于递推至真正的最小点，而非在附近停滞，教会了它细致的收敛控制。

长周期训练

先前学习型优化器的一大问题是短期偏向: 它们通常只在几十步内训练。为克服这一点，作者将训练步数从一个重尾分布中抽样，使优化器能够同时处理短期与长期训练过程的稳定性。

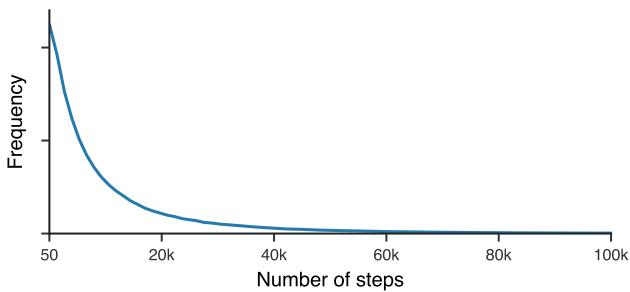
元训练期间每个任务的训练步数分布直方图。重尾分布确保优化器能适应长周期训练。

长时间展开训练让优化器在数千次迭代中保持稳定。

实验: 检验成果

经过元训练后，学习型优化器在实际任务中的表现如何？

主场任务: 元训练集

在用于训练的合成问题上，它始终匹敌或超越 ADAM 和 RMSProp。

学习型优化器在元训练样本问题上表现优于 ADAM 和 RMSProp。

图 3. 学习型优化器在训练任务上性能超过传统方法。

跨架构泛化

真正的突破发生在将优化器应用于未见过的任务时——例如在 MNIST 数据集上训练神经网络。尽管它在元训练中从未见过神经网络，仍能与经过精心调优的标准方法相媲美。

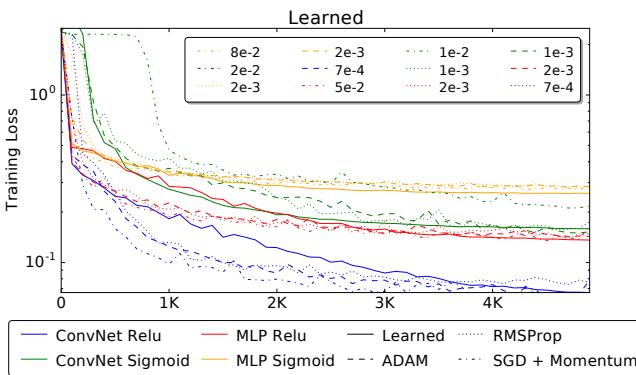
学习型优化器在未见过的神经网络架构上，与调优后的 ADAM、RMSProp 和 SGD 表现相当。

图 4a. 学习型优化器成功地在 MNIST 上训练了卷积网络和全连接网络。

扩展到 ImageNet

令人惊讶的是，该学习型优化器还能训练真正的大规模模型，如在 ImageNet 上的 InceptionV3 和 ResNetV2 。 在前 10,000–20,000 次迭代中，它的表现与专门调优的优化器相当。

学习型优化器能在 ImageNet 上训练大型模型，如 Inception V3 和 ResNet V2，其早期性能与调优优化器相当。

图 4b. 在 ImageNet 上的早期优化性能媲美最先进的手动优化器。

尽管训练后期性能趋于平稳，但一个在玩具问题上训练出来的学习型优化器能稳定地训练 ImageNet 级模型上千步，这是前所未有的成果。

学习率初始化的鲁棒性

选取合适的学习率常常令人头疼。然而，该学习型优化器在广泛的初始学习率下表现更稳定。

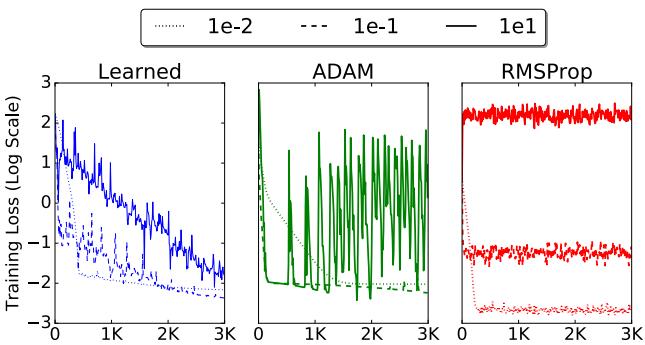
学习型优化器 (左) 在各种初始学习率下保持稳定，而 ADAM 和 RMSProp 敏感得多。

图 5. 学习型优化器在学习率设置上的泛化能力优于 ADAM 和 RMSProp。

消融实验: 每个特性都重要

移除任何关键组件 (如注意力机制、多时间尺度动量或对数元目标) 都会显著降低性能。每个部分都对稳定性与收敛性起到重要作用。

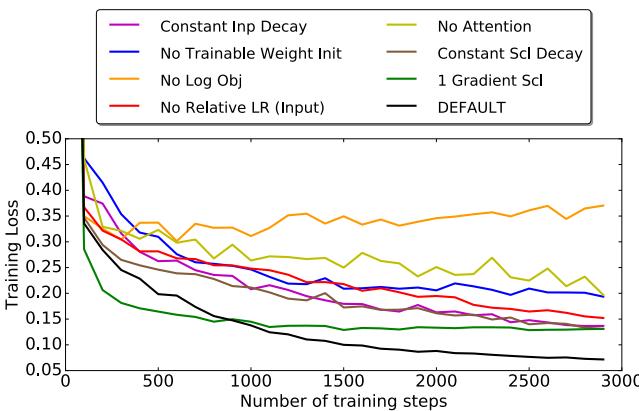
消融实验显示，移除关键特征 (彩色线) 会显著降低性能，完整模型 (黑色) 表现最佳。

图 6. 每个设计选择都增强了优化器的泛化与性能。

实际运行时间比较

虽然学习型优化器在小批量下开销较大，但随着批量规模增大，这一差距逐渐缩小。最终，其运行时间接近标准优化器。

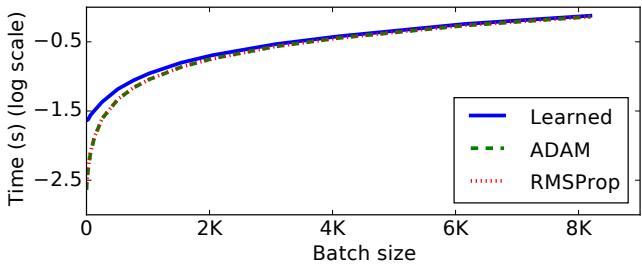
随着批量大小增加，每步优化的实际运行时间逐渐接近 ADAM。

图 7. 批量增大后运行时可扩展性显著提升，使学习型优化器在大型模型中具备实用性。

结论: 大规模学习如何学习

Wichrowska 及其团队实现了曾被认为不可能的目标: 开发出一种能够在全新任务间泛化、并可扩展至超大模型的学习型优化器。

其关键要素——分层 RNN 协调结构、融合优化经验的设计特征以及多样且长周期的元训练方案——共同赋予了优化器强大的通用学习能力。

尽管仍有挑战 (如在训练后期持续提升性能) ，这项研究已将学习型优化器从理论概念变为手工调优方法的有力继任者。

更深层的意义在于: 若我们能教人工智能优化任何事物——甚至优化它自身的学习过程——那么我们就更接近真正能学习如何学习的系统。

下一代优化器或许不再由人类直觉打造，而是由机器智能自主发现。