引言: 对数据的渴求

现代深度学习是一个奇迹——但它同时也是一个数据“吞噬者”。像大规模视觉和语言模型这样的系统依赖庞大的数据集，有时需要耗费数周的计算才能完成训练。当数据充足时，这种方法行之有效，但若数据稀缺，又该怎么办？例如，我们如何训练一个系统，仅凭几张照片就能识别稀有动物物种？又如何让机器人在只看过一次新物体后就能学会操作它？

这正是小样本学习 (few-shot learning) 的挑战所在: 让模型能够在极少的数据下实现泛化。人类在此方面天生擅长——给孩子看一张斑马的图片，他们即使只看过一次，也能再次认出斑马。而机器学习模型通常需要成千上万个样本。如何弥合这一差距，是人工智能最令人着迷的前沿之一。

关键思想在于从“学习”转向“学习如何学习”，也就是元学习 (meta-learning) 。 与其在单一的大数据集上训练模型，不如让一个“元学习器”在多个小而相关的任务上学习。这样，元学习器就能发现快速适应的基本原理——如何仅依靠少量样本高效地学习新任务。

本文深入探讨该领域的一项里程碑式工作: “Meta-SGD: Learning to Learn Quickly for Few-Shot Learning” 。 作者提出的方法不仅能学习一个优秀的模型起点，还能学习模型的更新方式。Meta-SGD 学习了一种属于自己的随机梯度下降 (SGD) 版本——专为快速适应而设计。令人惊讶的是，它仅需一次更新就能达到当前的最佳性能。

背景: 元学习的兴起

元学习通过两层互相关联的循环工作，分别运行在不同的时间尺度上:

  1. 内循环 (快速学习) : “学习器”模型在一个小且具体的任务上进行训练——例如，只用每类一张图片来分类五种新花卉。这个过程很快，通常只需一次或几次更新。
  2. 外循环 (慢学习) : “元学习器”观察这些学习器的适应过程，并评估其泛化能力。然后它调整自身参数，优化这一过程。在多个任务上不断重复后，元学习器逐渐掌握“学习”的普遍规律。

可以把内循环比作学生为一次突击测验快速掌握知识；外循环则是老师通过大量测验不断改进教学策略。

在 Meta-SGD 出现之前，研究者主要探索了三种类型的元学习方法:

  • 基于度量的方法 (如 Matching Networks、Siamese Networks) : 通过学习一个嵌入空间，使距离度量帮助模型用极少的标签对新样本进行分类。
  • 基于记忆的方法 (如 Memory-Augmented Neural Networks，简称 MANNs) : 使用像 LSTM 这样的循环结构来存储经验，实现快速回忆和利用。
  • 基于优化的方法: 直接学习如何训练模型——这正是 Meta-SGD 的核心。著名的 MAML (Model-Agnostic Meta-Learning) 学习一组权重初始化 \( \theta \)，使模型能在新任务上用标准 SGD 快速适应。

然而，MAML 仅学习了初始化 \( \theta \)。学习率以及更新方式仍需人工设定。Meta-SGD 的作者提出: 是否可以直接学习整个优化过程？

核心方法: 为梯度下降赋能

经典的随机梯度下降 (SGD) 通过以下公式更新参数 \( \boldsymbol{\theta} \):

\[ \boldsymbol{\theta}^{t} = \boldsymbol{\theta}^{t-1} - \alpha \nabla \mathcal{L}_{\mathcal{T}}\left(\boldsymbol{\theta}^{t-1}\right) \]

这一过程包含三个关键部分，传统上由人工设计:

  1. 初始化 (\( \boldsymbol{\theta}^{0} \)) —— 通常是随机的。
  2. 更新方向 (\( \nabla \mathcal{L_{\mathcal{T}}} \)) —— 即负梯度，表示最陡下降方向。
  3. 学习率 (\( \alpha \)) —— 决定步长大小的标量。

MAML 仅元学习了初始化 \( \boldsymbol{\theta} \)，而 Meta-SGD 更进一步: 它同时学习初始化、更新方向和学习率这三个要素 。

Meta-SGD 的更新方程，展示了 θ′ = θ − α 逐元素乘以损失函数的梯度。

Meta-SGD 的核心更新法则: 每个参数都有自己学习到的学习率和方向调节器。

直觉如下:

  • \( \boldsymbol{\theta} \): 元学习得到的初始化——为新任务提供强大起点。
  • \( \nabla \mathcal{L}_{\mathcal{T}}(\boldsymbol{\theta}) \): 针对特定任务训练样本的梯度。
  • \( \boldsymbol{\alpha} \): 一个与 \( \boldsymbol{\theta} \) 同维度的向量，在元训练期间学习，编码每个参数的学习率和符号。
  • \( \circ \): 表示逐元素乘法。

通过将学习率扩展为向量，Meta-SGD 产生了两个重要效果:

  1. 逐参数学习率: 每个权重都能学习自身最优步长。
  2. 可学习的更新方向: \( \boldsymbol{\alpha} \) 的各元素可以为负，从而调整标准梯度下降的方向。

这意味着 Meta-SGD 能引导优化过程朝向更好的泛化，而不是仅仅追求损失最小化。它本质上重新定义了“学习”这一过程——成为一个能学习如何优化的优化器。

一张图解 Meta-SGD 两层学习过程的示意图。渐进的 (θ, α) 元学习跨任务进行，而 θ 的快速适应在任务内完成。

元学习在跨任务间缓慢进行 (黑线) ，而快速适应在任务内部完成 (红箭头) 。Meta-SGD 同时学习初始化和更新策略。

元训练循环

在元训练阶段，模型通过最小化内循环更新后的期望测试损失，同时学习初始化 \( \boldsymbol{\theta} \) 和适应参数 \( \boldsymbol{\alpha} \)。

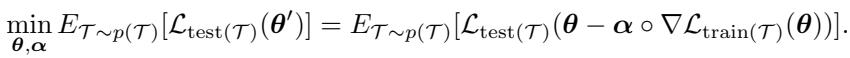
Meta-SGD 的元优化目标函数。

目标是最小化经过任务特定适应后在测试集上的期望损失。

具体过程如下:

  1. 采样一批任务 \( \mathcal{T}_i \sim p(\mathcal{T}) \)，每个任务拥有训练集和测试集。
  2. 内循环: 对每个任务，计算梯度 \( \nabla \mathcal{L}_{\text{train}(\mathcal{T}_i)}(\boldsymbol{\theta}) \)，并进行如下适应: \[ \boldsymbol{\theta}_i' = \boldsymbol{\theta} - \boldsymbol{\alpha} \circ \nabla \mathcal{L}_{\text{train}(\mathcal{T}_i)}(\boldsymbol{\theta}) \]
  3. 测试集评估: 计算 \( \mathcal{L}_{\text{test}(\mathcal{T}_i)}(\boldsymbol{\theta}_i') \)，衡量泛化效果。
  4. 外循环: 对累积的测试损失进行梯度下降，更新 \( (\boldsymbol{\theta}, \boldsymbol{\alpha}) \)。

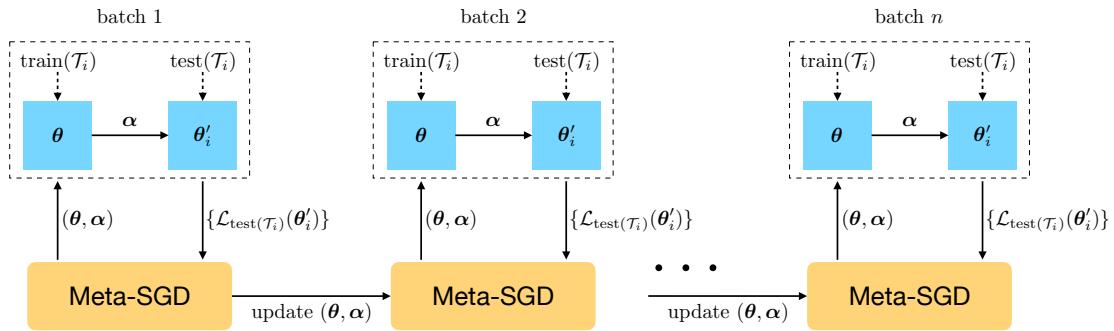
Meta-SGD 元训练过程示意图，展示了使用任务批次更新元参数 (θ, α)。

训练过程中，任务批次教会元学习器如何实现最优初始化与适应。

在监督学习场景下的 Meta-SGD 算法。

算法 1 概述了监督学习任务中的整体流程。

同样的原理也适用于强化学习——其中每个任务对应一个完整的马尔可夫决策过程 (MDP) ，损失为负的期望回报。Meta-SGD 学习初始策略及其在新环境中的适应规则。

在强化学习背景下的 Meta-SGD 算法。

算法 2 展示了 Meta-SGD 在强化学习中的应用，基于策略梯度进行更新。

实验与结果: 检验 Meta-SGD

作者在三个方向——回归、分类与强化学习——上测试了 Meta-SGD，并与 MAML 等强基线方法进行对比。

小样本回归

第一个实验是K-shot 回归: 仅根据 K 个数据点拟合一个正弦波。

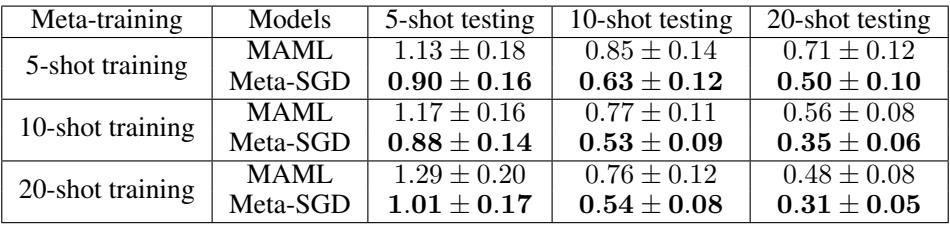
比较 Meta-SGD 和 MAML 在小样本回归任务上的表格。Meta-SGD 始终获得更低的均方误差。

表 1: Meta-SGD 相比 MAML 始终获得更低的均方误差 (Mean Squared Error) ，表明其适应能力更强。

Meta-SGD 的优势非常明显——在所有配置中均优于 MAML。通过同时元学习初始化与更新策略，它学得了一条能更好捕捉底层结构的优化路径。

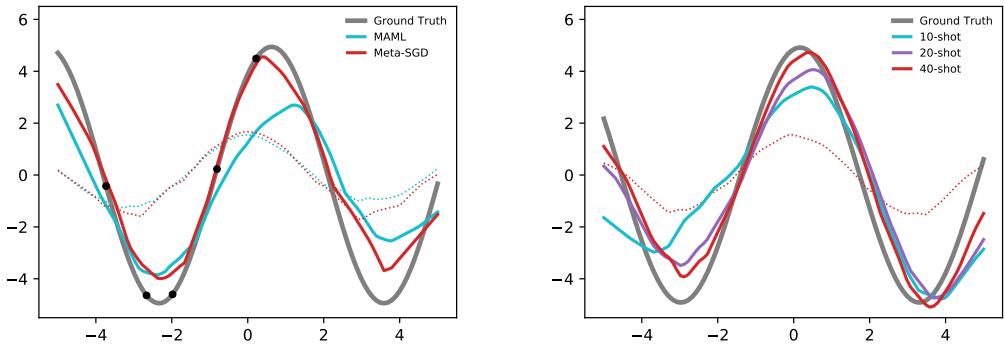
显示 Meta-SGD 与 MAML 在 5-shot 回归任务中的表现。Meta-SGD 的拟合曲线 (红色实线) 与真实波形高度一致。

图 3: 在数据有限的情况下，Meta-SGD 的适应效果更佳。仅一次更新后，红色曲线几乎与真实正弦波完全吻合。

在 5-shot 示例中 (左图) ，所有样本位于曲线一侧，MAML 难以泛化，而 Meta-SGD 则轻松学习到完整的正弦形状。这个自学习的优化器显然能在更具泛化性的方向上进行调整。

小样本分类

Meta-SGD 在两个重要的基准上进行了评估——Omniglot 和 MiniImagenet 。

Omniglot 是一个手写字符数据库，用于测试单样本与少样本识别:

Omniglot 数据集分类准确率表。Meta-SGD 略优于 MAML 与其他方法。

Meta-SGD 在 Omniglot 少样本分类上表现接近完美，略高于其他模型。

MiniImagenet 则将挑战扩展至真实世界图像:

MiniImagenet 数据集分类准确率表。Meta-SGD 显示出比其他方法更显著的性能提升。

Meta-SGD 在 MiniImagenet 上取得明显提升，大幅超越其他方法。

在两个数据集上，Meta-SGD 都能达到或超越当前的最佳准确率——并且只需一步适应即可完成。这使得它在应对新任务时异常高效，同时不损失性能。

小样本强化学习

在强化学习中，Meta-SGD 被用于 2D 导航任务: 智能体需要从起点移动至目标位置。

MAML 与 Meta-SGD 在 2D 导航任务上的平均回报表。Meta-SGD 获得更高 (负值更小) 的回报。

表 4: Meta-SGD 在 2D 导航任务中取得更高的平均回报，相比 MAML 表现更优。

使用 Meta-SGD 训练的智能体适应更快，获得更高的奖励。查看其轨迹可以解释这一差异:

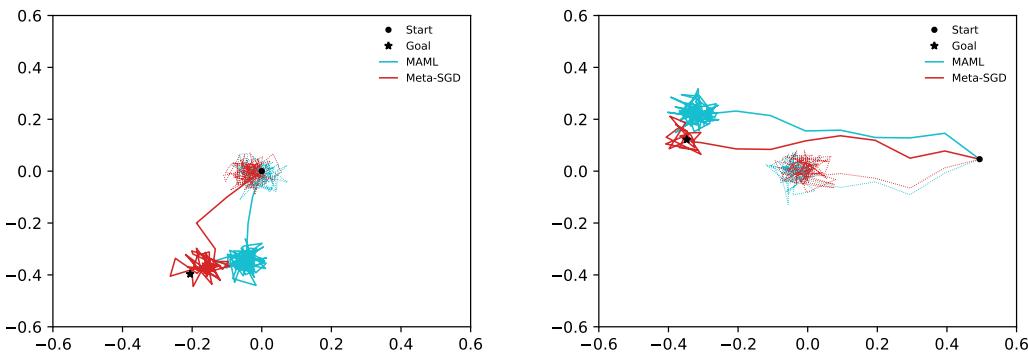
MAML (蓝色) 与 Meta-SGD (红色) 智能体轨迹可视化。Meta-SGD 的路径更直接、更高效地到达目标。

图 4: Meta-SGD 产生了更平滑、更直接的路径，策略更新更高效、更坚定。

这些结果显示，Meta-SGD 学习到的更新规则优于传统的梯度式适应，即使在动态环境中也能表现出色。

结论与启示

Meta-SGD 的研究提出了一种新的范式: 优化器不再需要人工设计，而可以通过学习而得。通过元学习初始化、方向以及逐参数学习率，Meta-SGD 构建出一个定制化优化过程，能够在不同任务间快速且有效地适应。

核心要点:

  • 更高能力: Meta-SGD 学习了优化过程的全部组成部分，超越了仅学习初始权重的 MAML。
  • 快速适应: 仅需一步更新就能实现顶级性能，具备即时学习能力。
  • 强通用性: 在回归、分类、强化学习等多领域均表现卓越。

Meta-SGD 为实现更自主的学习系统铺平了道路——让优化器能通过经验演化，而非依靠人工调整。未来的研究可探索如何将 Meta-SGD 扩展到更大规模模型和跨领域任务，使模型真正实现如人类认知般的“学会学习”。