人类拥有一种卓越的能力，仅凭一两个例子就能学会新概念。只要看过一张鸭嘴兽的照片，你很可能就能认出另一张——即便角度不同。现代人工智能，尤其是深度学习，在这方面却举步维艰。尽管这些模型在图像识别等任务上能取得超人般的表现，但它们通常需要海量数据集，每个类别都要包含成千上万个标注样本。人类和机器在学习能力上的差距，是我们构建灵活、可适应的人工智能系统时面临的主要障碍。

小样本学习 (few-shot learning) 领域旨在通过设计能从少量标注样本中泛化的模型来缩小这一差距。一种流行的思路是 元学习 (meta-learning) , 即 学习如何学习，让模型在大量小型学习任务上进行训练以掌握通用的适应策略。然而，大多数小样本学习的研究都假设所有数据都有标签。那么，如果我们除了少量标注样本外，还有大量的 无标签 数据呢？这种场景不仅更贴近现实——也更接近人类在复杂、无标签的环境中学习的方式。

来自多伦多大学、谷歌大脑和麻省理工学院的研究者在2018年发表了一篇论文探讨这个问题。在《元学习在半监督小样本分类中的应用》一文中，作者们将小样本学习范式扩展到一个更实际的半监督场景，展示了模型如何利用无标签数据——包括不相关的“干扰”图像——显著提升预测性能。这项研究标志着朝着构建能像人类一样以最少监督进行学习的人工智能迈出了重要一步。

图1: 半监督小样本学习问题的直观表示。给定一个小的有标签支持集 (如金鱼和鲨鱼) ，目标是利用一个大的无标签图像集来帮助分类新的、未见样本。无标签集中既包含相关样本 (红色边框) ，也包含其他类别的无关干扰项。

图1: 半监督小样本设置。学习器拥有两种鱼类的标注样本，以及一个包含大量无标签海洋生物 (包括无关干扰项) 的数据池。

背景: 用原型网络学习如何学习

要理解这项研究的创新，我们首先需要回顾小样本学习的基础及其最具影响力的模型之一——原型网络 (Prototypical Networks) 。

分集式训练范式

现代小样本学习通常采用 分集式训练 (episodic training) , 即在元训练过程中反复模拟小样本场景。模型不是一次性在整个数据集上训练，而是进行许多小的 *分集 (episodes) *，每个分集都是一个独立的小型分类任务。

每个分集包含:

  1. 支持集 (S): 一个小型有标签训练集，包含 N 个类别，每个类别有 K 个样本。
  2. 查询集 (Q): 一组来自 相同 N 个类别的无标签样本，用于在该分集内评估。

模型通过支持集的标注样本学习去分类查询样本。损失函数根据查询集上的预测结果计算，并通过梯度更新参数。大量随机化的分集训练过程让系统学会如何构建有效的小样本分类器——本质上，就是 学习如何学习。

原型网络 (ProtoNets)

由 Snell 等人 (2017) 提出的 原型网络 为小样本分类提供了简洁而有效的解决方案。其核心思想是将输入嵌入到特征空间中，使得同类样本彼此接近。

  1. 嵌入 (Embedding): 神经网络将每个输入图像 \(x\) 映射到嵌入空间中的向量 \(h(x)\)，使相似类别自然聚集。

  2. 原型计算 (Prototype Calculation): 对于支持集中的每个类别 \(c\)，模型计算一个 原型向量——即该类别所有样本嵌入的均值。

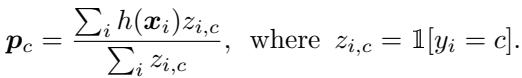
公式1: 类别 c 的原型是其支持样本嵌入的平均值。指示函数 \\(z_{i,c}\\) 在样本 \\(i\\) 属于类别 \\(c\\) 时取值为 1。

公式1: 基于类别嵌入均值的原型计算。

  1. 分类 (Classification): 为了分类新的查询样本 \(x^*\)，模型将其嵌入为 \(h(x^*)\)，并计算它到每个类别原型的距离。样本属于类别 \(c\) 的概率通过对负距离的 softmax 得出——距离最近的原型通常获胜。

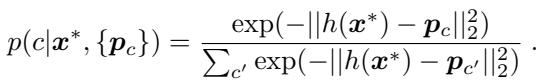
公式2: 查询样本属于类别 c 的概率由其与所有原型间的平方欧氏距离的 softmax 计算得到。

公式2: 基于原型距离的查询样本分类。

整个分集的损失是所有查询样本上正确预测的负对数概率的均值:

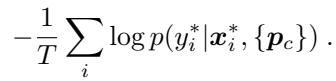
公式3: 分集损失是查询样本预测类别与真实类别之间的交叉熵。

公式3: 训练原型网络的优化目标。

原型网络的简洁之美在于: 它学习了一个良好的度量空间，使类别簇易于形成与比较。

半监督小样本学习

作者们通过在每个分集中引入第三个部分来扩展该框架: 一个 无标签集 \(\mathcal{R}\)，其中包含没有标签的样本。

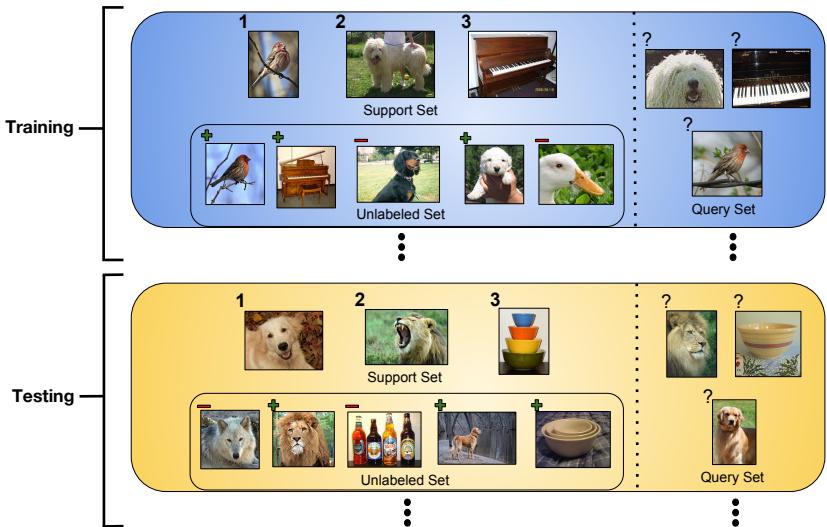
图2: 半监督小样本设置示意图。每个分集包含一个有标签支持集、一个无标签集和一个查询集。无标签集中可能有相关样本 (绿色加号) 和无关样本 (红色减号) ；模型并不知道哪些是相关的。

图2: 半监督训练和测试分集均包含来自相关类别和干扰类别的无标签样本。

关键在于如何利用这些无标签样本——其中一些属于支持集的同类，另一些则是干扰项。作者提出的解决方案是: 利用无标签数据来 优化原型 , 即在最初计算的有标签原型基础上进行细化。这些改进后的原型在查询阶段能获得更好的泛化能力。

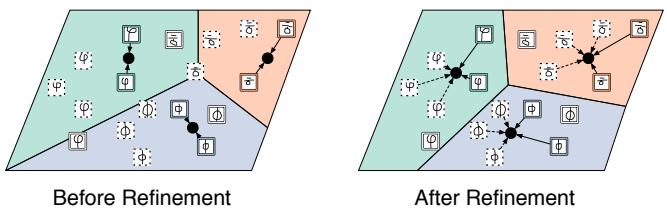
图3: 原型优化示意图。左: 仅基于有标签数据的初始原型。右: 优化后的原型融合了无标签样本，使决策边界更准确。

图3: 使用无标签样本进行原型优化。

论文提出了三种逐步增强的优化策略。

1. 使用软 k-均值优化原型

最简单的方法借鉴了 软 k-均值聚类 (soft k-means clustering) 。 原型被视为聚类中心，无标签点则被以概率形式分配到这些聚类中。原型随后更新，以更好地代表所有相关样本——包括有标签和无标签的。

流程概述:

  1. 初始化原型: 使用有标签样本计算初始原型。
  2. 计算软分配: 基于与原型的距离，为每个无标签样本分配其属于各类别的概率。
  3. 优化: 将有标签 (硬分配) 和无标签 (软分配) 样本的加权平均用于更新原型。

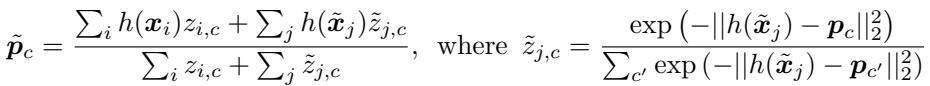
公式4: 优化后的原型通过有标签和无标签样本的加权平均计算，其中软分配权重反映每个无标签样本的预测类别概率。

公式4: 通过软 k-均值进行原型优化。

实验发现，只需一次优化步骤即可显著提升性能。

2. 通过额外簇处理干扰项

软 k-均值假设所有无标签样本都属于已知的 \(N\) 个类别之一。但在现实中，许多无标签样本可能是干扰项，会干扰原型，使其偏向无关区域。

为防止这种情况，作者引入一个 额外的干扰簇 。 这个第 \((N+1)\) 个簇专门用于捕获不属于任务类别的无标签样本，吸收离群点，防止其影响真实类别原型。

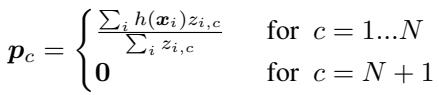
公式5: N+1 个簇的初始原型。前 N 个来自有标签样本，干扰簇原型位于原点。

公式5: 新增干扰簇以处理不相关样本。

每个簇的 长度尺度 (length-scale) (\(r_c\)) 可单独调整，使干扰簇能更宽泛地分布，容纳各种离群点而不破坏主要结构。

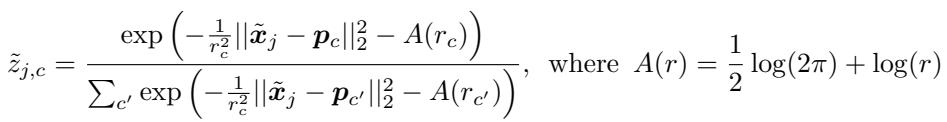
公式6: 更新后的软分配公式，加入了干扰簇及可调的长度尺度 \\(r_c\\)。

公式6: 为增强对干扰项的鲁棒性而修改的软分配方法。

3. 更复杂的方法: 掩码软 k-均值

最后也是最先进的扩展是 掩码软 k-均值 (Masked Soft k-Means) , 它学会 选择性地忽略 干扰项。与将所有离群点归入一个簇不同，网络学习一个 掩码 来决定每个无标签样本对原型的影响程度。

步骤如下:

  1. 归一化距离: 对每个无标签样本–原型对，计算归一化距离 \( \tilde{d}_{j,c} \)。

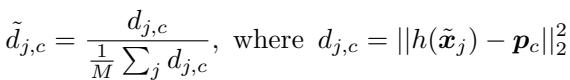
公式7: 无标签样本与原型间距离的归一化。

公式7: 用于自适应掩码的归一化距离。

  1. 预测掩码参数: 一个小型 MLP 通过分析距离的统计特征 (例如最小值、最大值、方差、偏度、峰度) ，为每个类别预测阈值 \(\beta_c\) 和斜率 \(\gamma_c\)。

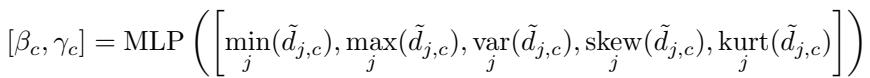
公式8: MLP 根据距离分布的统计特征输出自适应阈值和斜率参数，用于掩码计算。

公式8: 学习自适应掩码参数。

  1. 计算掩码并优化: 每个无标签样本通过 sigmoid 函数得到一个掩码值 \(m_{j,c}\)。若它接近该原型 (距离低于阈值) ，掩码值接近 1；否则接近 0。在计算新原型时，这些掩码值作为权重影响样本贡献。

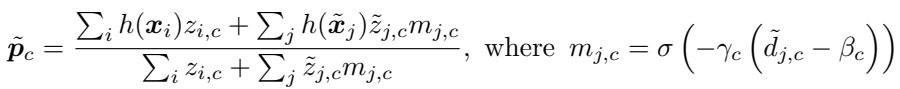
公式9: 最终的优化公式，同时使用软分配和学习到的掩码值加权无标签样本的贡献。

公式9: 使用学习到的掩码进行原型优化以排除干扰项。

由于整个过程均可微分，MLP 与优化过程可以联合训练。于是，模型不仅学习了嵌入空间，还学习了过滤不相关无标签数据的原则性方法。

实验与结果

作者在三个数据集上验证了该框架:

  • Omniglot: 来自 50 种字母的手写字符。
  • miniImageNet: ImageNet 的简化版，常用于小样本学习基准测试。
  • tieredImageNet: 本文提出的更大且层次化组织的数据集，确保训练与测试类别相互独立。

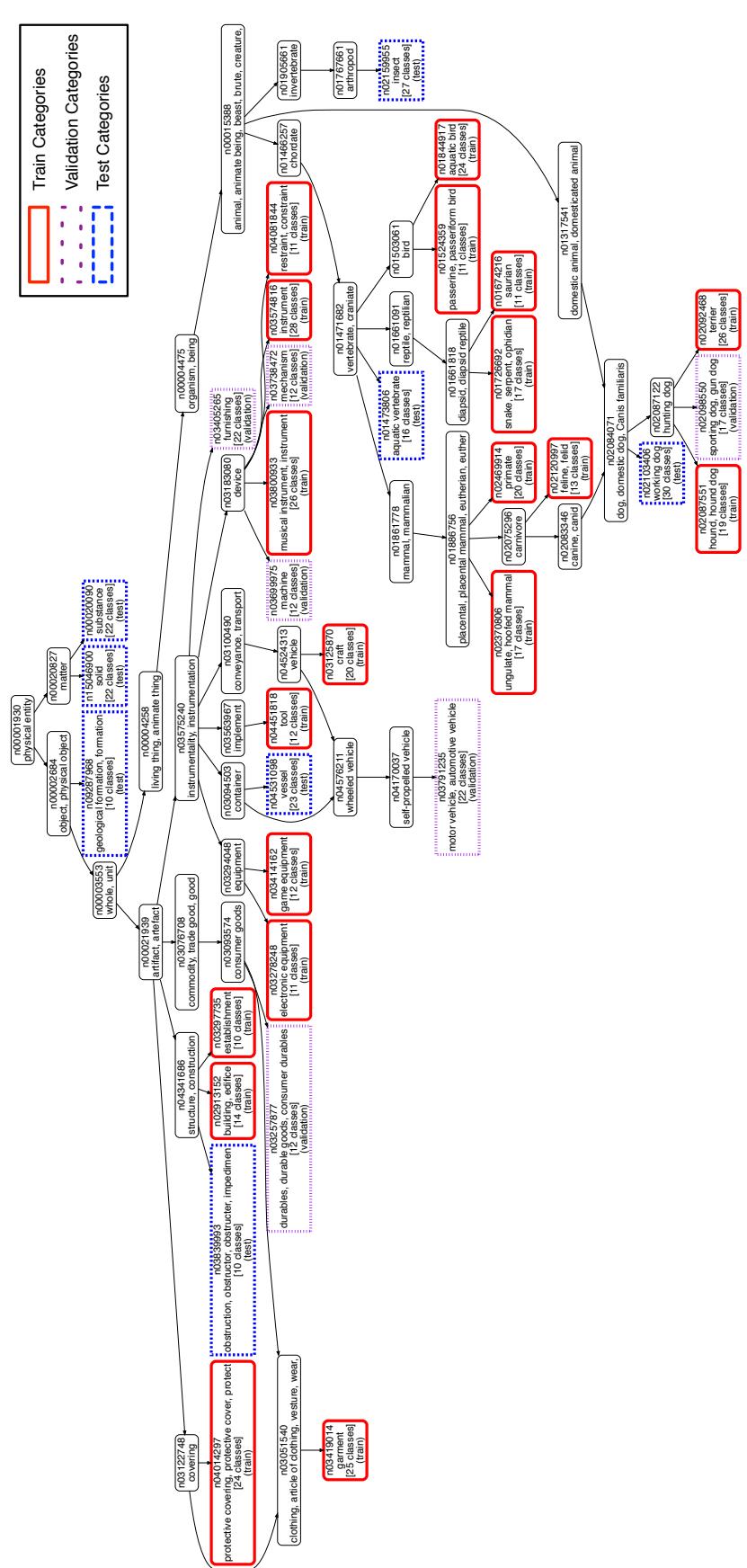
图5: tieredImageNet 的层次结构。训练类别 (红色) 和测试/验证类别 (蓝色) 在高层级上分离，避免出现过于相似的训练–测试配对 (如两种狗) 。

图5: tieredImageNet 的层级化类别划分，确保训练和测试类别之间的有效差异。

基线对比:

  1. 监督学习 (Supervised) : 标准原型网络，忽略无标签数据。
  2. 半监督推理 (Semi-Supervised Inference) : 一个监督训练的原型网络，在测试阶段通过一次 k-均值步骤进行优化。

在所有数据集上，半监督变体的性能都有显著提升。

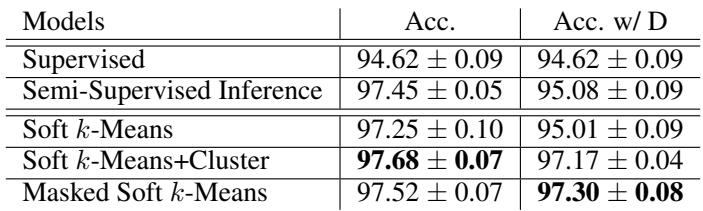
表1: Omniglot 的 1-shot 分类准确率。“w/ D” 表示无标签集中包含干扰项。

表1: Omniglot 的结果显示，半监督优化显著提升了性能。

表2: miniImageNet 的 1-shot 与 5-shot 分类准确率。

表2: 在 miniImageNet 上，半监督方法的表现明显优于基线模型。

表3: tieredImageNet 的 1-shot 与 5-shot 分类准确率。

表3: tieredImageNet 的结果验证了即使存在干扰项，使用无标签数据仍然有明显优势。

主要发现:

  1. 无标签数据有帮助: 所有半监督模型的表现均优于监督基线，充分证明无标签样本能增强小样本学习。
  2. 元训练的重要性: 端到端地学习优化原型的方法比仅在推理阶段优化的模型更优，表明“学习如何优化原型”本身是有益的。
  3. 掩码 k-均值在干扰条件下表现出色: 掩码模型能稳健地处理未见类别，在有噪声数据下的表现几乎与干净数据条件持平。

随着测试时可用无标签样本数量的增加，模型性能持续提升——甚至超出训练条件——显示出强泛化能力。

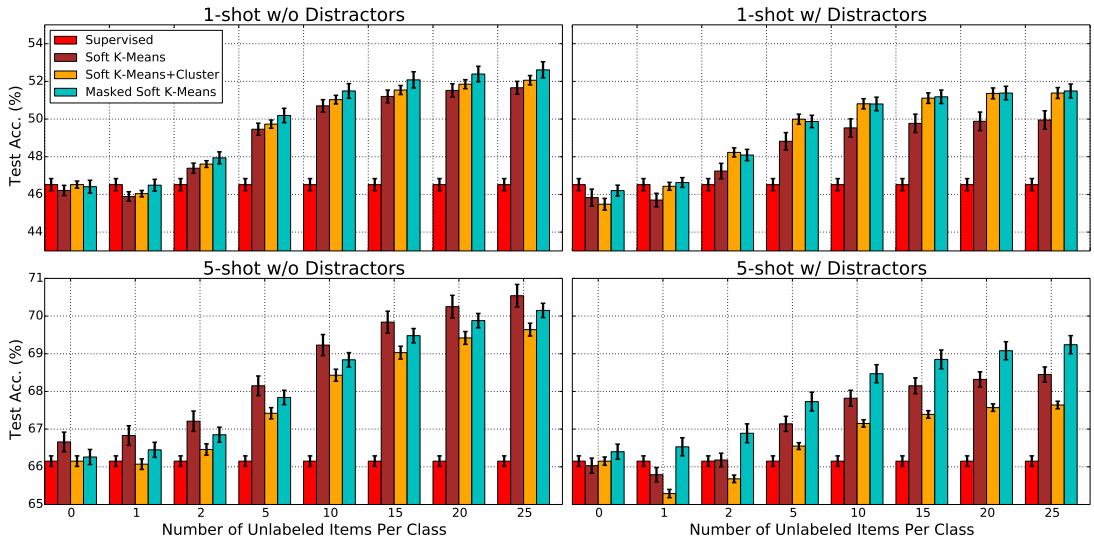
图4: 在 tieredImageNet 上，随着每类无标签样本数量增加，准确率持续提高，所有半监督方法均能有效利用额外数据。

图4: 随着每类无标签样本增多，准确率稳定提升。

进一步分析学习到的掩码分布发现其呈现 双峰特征 : 掩码值集中在 0 或 1 附近，表明模型能自信地区分有效样本与干扰项。

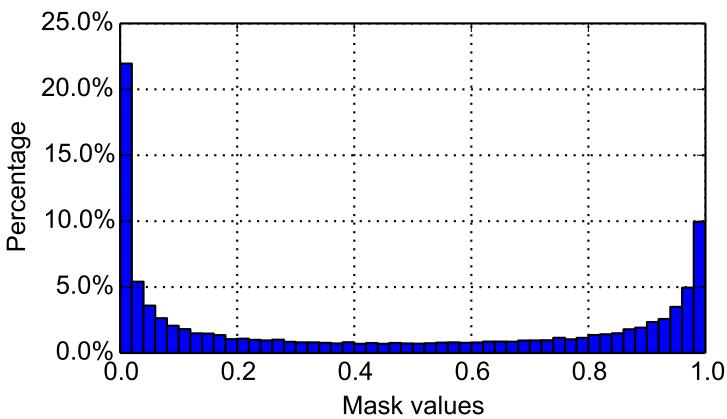
图7: 在 Omniglot 上，掩码软 k-均值模型预测的掩码值分布图。多数值接近 0 或 1，显示对相关与干扰样本的明确区分。

图7: 在 Omniglot 上学到的掩码分布，显示出清晰的包含–排除行为。

结论与启示

这项研究将小样本学习拓展到更贴近现实的半监督领域，连接了 元学习、半监督学习 和 聚类 。 结果表明，无标签数据——即使带有噪声或不完美——只要合理整合，都能显著提高模型的准确率。

关键启示:

  • 新的学习框架: 首次给出了半监督小样本学习的正式定义和基准适配。
  • 优化模型: 三种原型网络扩展，能高效利用无标签数据，其中掩码软 k-均值最具鲁棒性。
  • 更强的基准: tieredImageNet 引入结构化划分，更能反映真实世界场景。

通过学习在每个任务中从无标签样本中获益，这些模型展现了人类般的适应能力。在一个数据泛滥而标注稀缺的世界中，此类方法为更智能、更高效的人工智能铺平道路——即使在监督极少时也能茁壮成长。