你是否曾看过一张陌生动物 (比如水豚) 的图片，之后就能在不同的照片中认出它？人类拥有一种惊人的能力，仅凭一个或少数几个例子就能学会新概念。这正是小样本学习的精髓，而这一能力长期以来一直是人工智能领域的重大挑战。

现代深度学习模型在训练海量数据集 (例如数百万张猫的图片) 时表现卓越，但当给它们的样本量很小时，它们却很难胜任。一个仅用五张新犬种图片训练的深度神经网络很可能出现过拟合，它会记住这些特定图片，而不是学习该犬种的通用特征。

为了解决这个问题，研究者提出了一种名为元学习 (meta-learning) 或“学会学习”的范式。其核心思想是在不同的学习任务上训练模型，让它能快速适应以前从未见过的新任务。不过，许多元学习方法 (如广受影响的 MAML——模型无关元学习) 往往必须使用较浅的网络结构来避免过拟合，因而未能充分挖掘深度架构的潜力。

这时，论文 Meta-Transfer Learning for Few-Shot Learning 问世了。作者提出了一种巧妙的新方法，将两种思路的优势结合在一起。它利用了在大型数据集上预训练的深度网络的强大能力( 迁移学习 )，并结合了元学习的快速适应性。所提出的元迁移学习 (MTL) 方法能够学习如何细微地调整一个预训练的深度网络，使其能仅靠少量样本就掌握全新任务。

在本文中，我们将深入剖析这项研究，探讨:

  • 元学习和迁移学习的核心概念；
  • MTL 的两项关键创新: 缩放与移位 (SS) 操作，以及 困难任务 (HT) 元批次训练策略；
  • 这些思想如何帮助深度网络在具有挑战性的小样本基准上取得最先进的结果。

泡杯咖啡，让我们一起探索如何让我们的模型像人类一样高效地学习。

奠定基础: 从迁移学习到元学习

在深入了解 MTL 之前，让我们先弄清它所建立的理论背景。论文给出了一个非常有帮助的概念性比较框架。

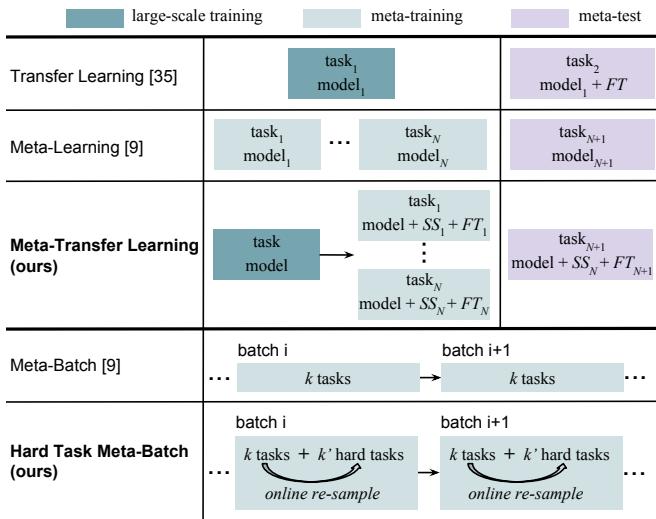
迁移学习、元学习和元迁移学习 (MTL) 及困难任务 (HT) 元批次策略的概念性比较。

图 1: MTL 通过学习用于适应预训练深度网络的轻量级缩放与移位参数，将迁移学习与元学习元素相融合。

迁移学习: 这种经典方法从一个在 ImageNet 等海量数据集上预训练的模型开始。通常替换最后一层，然后在较小的目标数据集上进行微调 。 之所以有效，是因为早期层通常学习到通用特征，如边缘或纹理。然而，当目标数据集很小时，全面微调仍可能导致过拟合。

元学习: 与其在样本上训练，元学习是在任务层面上进行的。每个任务 (也称为一个 episode) 都有一个小的训练集 (支持集) 和一个测试集 (查询集) 。一个“5-way, 1-shot”任务表示:

  • 模型会看到 5 个新类别；
  • 每个类别仅提供 1 个样本进行学习；
  • 模型必须对来自这 5 个类别的新样本进行分类。

通过在数千个这样的任务上训练，模型学会了可迁移到未见任务的通用学习机制。MAML 就是这方面的典型例子，它旨在学习能够快速适应新任务的良好初始化参数。

MTL 的作者意识到，可以通过设计一种对深度网络参数进行调制而非微调的方式，将迁移学习的高效性与元学习的适应性结合起来。

MTL 流程: 三阶段方法

元迁移学习遵循一个清晰的三阶段流程: 从大规模预训练，到元学习阶段，再到最终测试。

元迁移学习的三阶段流程: (a) 大规模 DNN 训练，(b) 元迁移学习，(c) 元测试。

图 2: 所提出的 MTL 方法的整体流程。

阶段 1: 构建坚实基础 (大规模训练)

这一阶段从标准的监督训练开始。作者使用深度卷积网络 (例如 ResNet-12) ，在一个大规模分类任务上进行训练——例如使用 miniImageNet 的 64 个类别，每个类别包含 600 张图片。

记 Θ 为特征提取器 (卷积层) ，θ 为分类器 (最后一层全连接层) 。它们通过梯度下降更新:

\[ [\Theta;\theta] := [\Theta;\theta] - \alpha \nabla \mathcal{L}_{\mathcal{D}}([\Theta;\theta]) \]

损失函数基于数据集样本 \((x,y)\) 计算:

\[ \mathcal{L}_{\mathcal{D}}([\Theta;\theta]) = \frac{1}{|\mathcal{D}|} \sum_{(x,y)\in\mathcal{D}} l(f_{[\Theta;\theta]}(x),y) \]

训练完成后，特征提取器 Θ 成为一个稳固的基础，能够表示通用视觉模式。重要的是，这些权重将被冻结，在后续元学习过程中不再改变。而初始分类器 θ 会被舍弃，因为每个小样本任务涉及不同类别。

阶段 2: 核心创新——元迁移学习

现在进入最关键的部分。问题是: 如何在不改变已冻结的特征提取器 Θ 权重的情况下，让它适应新的小样本任务？

答案是: 缩放与移位 (SS) 。

在 MTL 中，不再微调卷积权重 W 或偏置 b，而是为每个卷积层学习两个小的、任务专属的参数:

  1. 缩放参数 \( \Phi_{S_1} \)，用于对权重进行倍乘；
  2. 移位参数 \( \Phi_{S_2} \)，用于调整激活输出。

卷积操作从 \(WX + b\) 转变为:

\[ SS(X; W, b; \Phi_{S_{\{1,2\}}}) = (W \odot \Phi_{S_1})X + (b + \Phi_{S_2}) \]

其中 \(\odot\) 表示逐元素乘法。换句话说，网络学会了如何在不修改原始权重的前提下，细微地增强或抑制特征。

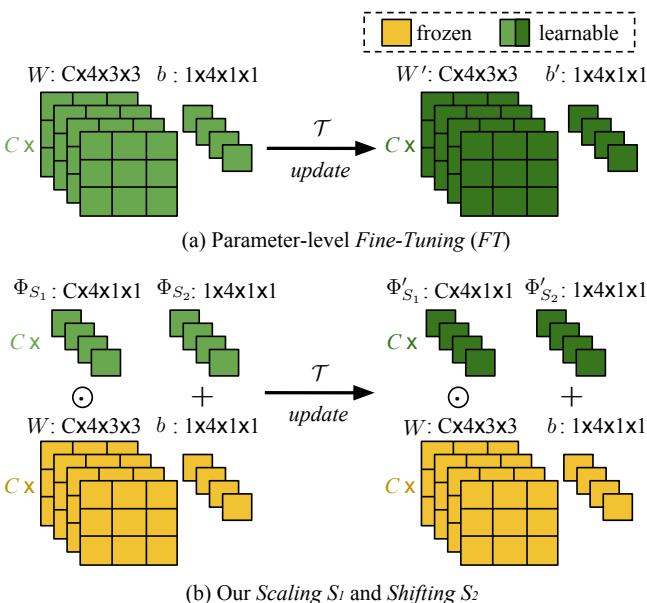
传统参数级微调 (FT) 与所提出的神经元级缩放与移位 (SS) 操作的比较。

图 3: 微调会影响所有滤波器参数，而 SS 仅为每个滤波器学习一个缩放与移位参数，极大降低了过拟合风险。

微调 (FT) 与 缩放与移位 (SS) 的区别相当显著:

  • FT 调整滤波器中的每个权重和偏置 (例如，3×3 滤波器有 9 个参数) ；
  • SS 每个滤波器仅学习两个轻量参数 。

这带来了三大优势:

  1. 高效性: 可学习参数非常少，适合小样本学习；
  2. 稳定性: 冻结的预训练权重能避免灾难性遗忘；
  3. 快速性: 从良好的初始化出发，加速了学习过程。

元训练循环内部

在元训练期间，MTL 同时优化分类器 θ 和 SS 参数。对每个任务 \(\mathcal{T}\):

  1. 基础学习器更新 (内循环) :
\[ \theta' \leftarrow \theta - \beta \nabla_{\theta} \mathcal{L}_{\mathcal{T}^{(tr)}}([\Theta;\theta], \Phi_{S_{\{1,2\}}}) \]

该步骤在不修改冻结的 Θ 的情况下，用任务的训练集调整分类器。

  1. 元学习器更新 (外循环) :

将更新后的分类器 θ' 在测试集上进行评估，并利用损失梯度更新元参数:

\[ \Phi_{S_i} := \Phi_{S_i} - \gamma \nabla_{\Phi_{S_i}} \mathcal{L}_{\mathcal{T}^{(te)}}([\Theta; \theta'], \Phi_{S_{1,2}}) \]\[ \theta := \theta - \gamma \nabla_{\theta} \mathcal{L}_{\mathcal{T}^{(te)}}([\Theta; \theta'], \Phi_{S_{\{1,2\}}}) \]

这种循环在数千个任务上不断重复，使 SS 层学会在不同的小样本场景中泛化。

历经磨砺更强大: HT 元批次

随机采样任务可以训练模型，但 MTL 引入了一个聪明的变体——受课程学习与困难样本挖掘启发的困难任务 (HT) 元批次策略。

HT 元批次让模型在最困难的任务上进行再训练:

  1. 先运行若干常规元批次；
  2. 从每个任务中找出准确率最低的“失败类别”；
  3. 重新抽样，聚焦这些更难的类别形成新任务；
  4. 在这个“困难批次”上再次训练。

该方法主动让模型面对困难任务，“在挑战中成长”。如图 1 所示，HT 元批次构建了一个有结构的训练序列，将学习动力集中在最需要的地方。

阶段 3: 元测试

元训练结束后，SS 参数保持固定。模型只在新的未见任务中调整小分类器，并在其查询集上评估性能。最终在数百个任务上的平均准确率即为最终指标。

结果: MTL 的表现如何？

在 miniImageNet 和 Fewshot-CIFAR100 (FC100) 数据集上的实验表明，MTL 不仅提高了准确率，还显著加快了训练收敛。

元学习优于简单微调

消融实验揭示了 MTL 元学习方法的重要性。如下图所示，带有 SS 的 MTL 明显优于仅用简单微调或传统训练的基线模型。

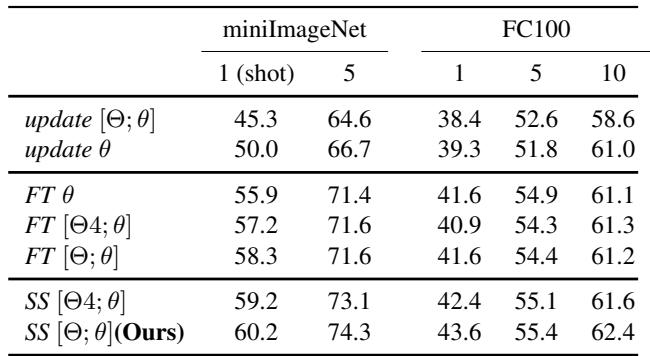
在 miniImageNet 和 FC100 上的消融实验结果，展示了 MTL 各组件的有效性。

表 1: MTL (底部几行) 始终优于更简单的基线模型。

在 miniImageNet 的 1-shot 任务中，MTL 取得了 60.2% 的准确率，而一个非元学习的基线模型 (update θ) 仅为 50.0% 。

在 miniImageNet 上的最新表现

结合 HT 元批次策略的 MTL 达到了顶级性能，超越了 MAML 和其他方法。

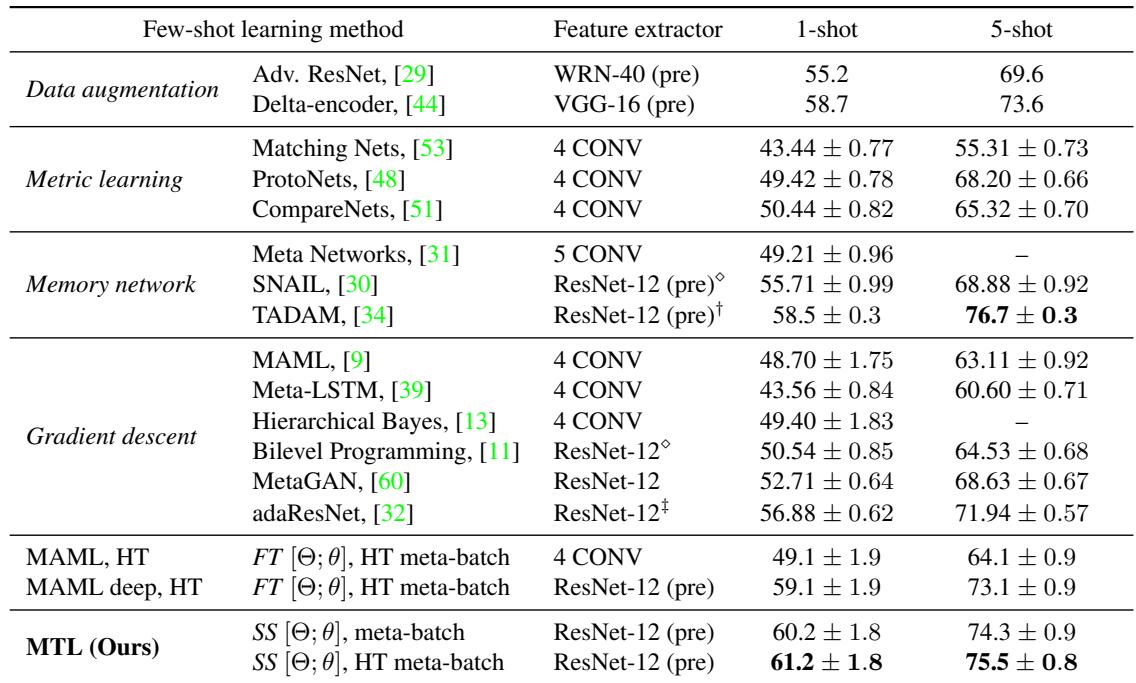
miniImageNet 数据集上 5-way 分类准确率的比较。

表 2: miniImageNet 上的性能表现。MTL 在具有挑战性的 1-shot 任务中取得了最高准确率。

  • MTL (ResNet-12 + HT 元批次): 61.2% (1-shot), 75.5% (5-shot)
  • MAML (ResNet-12): 59.1% (1-shot), 73.1% (5-shot)
  • 此前 SOTA (TADAM): 58.5% (1-shot), 76.7% (5-shot)

提升在最困难的 1-shot 情境中尤为明显。

FC100 上的稳健表现

FC100 按“超类” (如哺乳动物 vs. 昆虫) 划分类别，这对泛化能力提出了更大挑战。MTL 仍然表现优异。

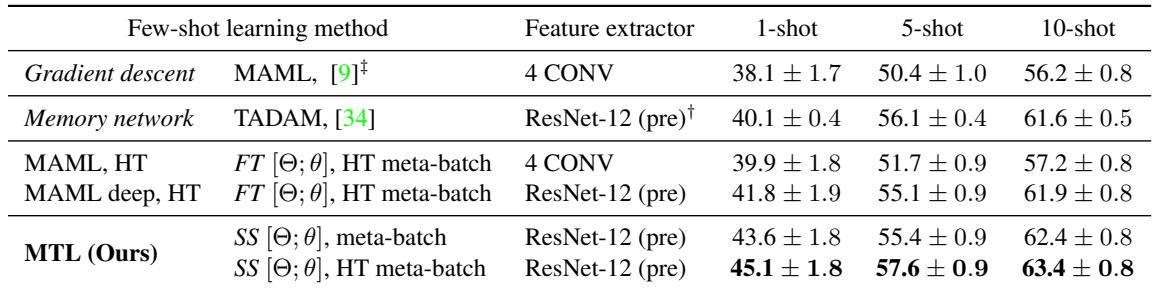
Fewshot-CIFAR100 (FC100) 数据集上的 5-way 分类准确率比较。

表 3: 在 FC100 上的结果。MTL 在所有小样本设置中都保持显著优势。

在各类任务中，MTL 相比 MAML 提升约 7% , 并在 1-shot 任务中比 TADAM 高出 5% 。

HT 元批次带来的加速学习

HT 元批次不仅提升表现，还加快收敛速度。下图展示了准确率随训练迭代次数的变化。

使用与不使用 HT 元批次的 MTL 准确率随训练迭代次数变化情况。

图 4: HT 元批次 (橙色曲线) 在不同数据集上都带来了更高准确率与更快收敛速度。

MTL 仅用 8,000 个任务就达到了高性能，而 MAML 需要 240,000 个任务——训练量减少了 30 倍。

结论: 更智能的适应之道

论文 Meta-Transfer Learning for Few-Shot Learning 展示了迁移学习与元学习的结合如何通过学习轻量级的适应规则，而非重新训练沉重的网络结构，从而让深度模型在小样本任务上焕发强大能力。

关键要点:

  1. 调制，而非重训练: 缩放与移位操作提供一种稳健、参数高效的适应方式，过拟合风险极小。
  2. 从强大基础出发: 利用预训练的深度网络为后续任务提供坚实起点，加速学习并提升泛化能力。
  3. 从失败中成长: 困难任务元批次让模型直面弱点，从而实现更快、更强的学习。

通过融合迁移学习与元学习，MTL 展现了人工智能如何能以人类般的效率学习新概念——更快、更聪明，并且需要更少的样本。