人类拥有一种非凡的能力，可以仅通过少量样本就学会新概念。给孩子看一次斑马的图片，他们很可能就能在野外、动画片或其他照片中认出斑马。这就是少样本学习的精髓——一种我们与生俱来但对机器而言历来是巨大挑战的能力。

传统的深度学习模型是出了名的“数据饥渴”。它们往往需要成千上万甚至数百万的样本才能掌握一项任务。当面临新问题且数据有限时，它们常常力不从心，无法从仅有的少量样本中实现泛化。这时, 元学习 (或称“学会学习”) 便派上用场。元学习模型不是从零开始学习单个任务，而是从各种任务中学习，从而形成一种学习的策略，帮助它能够快速适应新的、未知的任务。

该领域最受欢迎的方法之一是模型无关元学习 (MAML) 。 MAML 的核心思想是找到一组好的初始模型权重——一个强大的起点。从这样的初始化出发，模型只需在新任务上进行几步梯度下降，就能快速实现适应。这就好比在山上找到了一个完美的营地，从那里可以轻松攀登各种山峰。

但如果我们不仅能学到营地的位置呢？如果我们还能学到最佳的登山路径——即通往任何山峰的最优路线呢？这正是论文《元学习跨任务共享的学习趋势》所探讨的核心问题。研究者提出了一种名为路径感知元学习 (PAMELA) 的新方法，它不仅学习一个好的起点，还学习在适应过程中“如何行进”。它能捕捉更新方向、学习率及其随时间的演化——从而学习整个学习轨迹。

本文将深入探索 PAMELA: 我们将分析以往方法的局限性，剖析 PAMELA 的工作原理，并了解这种创新方法如何在少样本学习领域树立新标杆。

基于梯度的元学习格局

要理解 PAMELA 的创新，我们需先了解它的前辈——尤其是 MAML 及其扩展。这些方法属于基于梯度的元学习范畴，通常包含两个嵌套循环: 一个用于任务特定适应的内循环 , 一个用于总体元学习的外循环 。

想象你正在训练一个图像分类模型。不是用一个包含猫和狗的大型数据集，而是构建数百个小任务。每个任务可能是 5-way, 1-shot 类型: “这里有一张猫、一张狗、一张鸟、一辆车和一架飞机的图片，现在请识别属于这些类别的新图片。”

  • 内循环: 对于每个小任务，从当前的元学习权重 \( \theta \) 出发，在该任务的小训练集上执行几步梯度下降，使通用模型适应此任务的特定特征，从而生成任务特定权重 \( \theta' \)。
  • 外循环: 然后在任务的独立验证集上评估 \( \theta' \)，根据验证误差更新原始权重 \( \theta \)，使模型在未来任务中的适应更有效。

由此，目标是找到一个高度可适应的初始化 \( \theta \)——一组权重，使得模型能自然地实现快速学习。

MAML 与 Meta-SGD: 从好起点到更聪明的步伐

MAML 专注于学习初始化，在适应过程中使用固定学习率的简单梯度下降。其“元”智能仅体现在初始权重上。

Meta-SGD 则进一步扩展了这一思路，为每个参数学习独立的学习率，相当于进行梯度预处理——在参数空间中更高效地移动。

然而，两者都存在局限: MAML 的内循环是静态的，而 Meta-SGD 为所有步骤共享一个固定的预处理矩阵。事实上，学习过程应当随时间变化: 早期应有大的探索性更新，后期应逐步微调。MAML 与 Meta-SGD 均未能捕捉这种动态趋势。

PAMELA 简介: 学习整个路径

PAMELA 通过让学习过程本身变得动态且可学习，克服了上述局限。它不再使用固定的优化规则，而是学习在内循环的各个步骤中，学习的轨迹应如何演变。

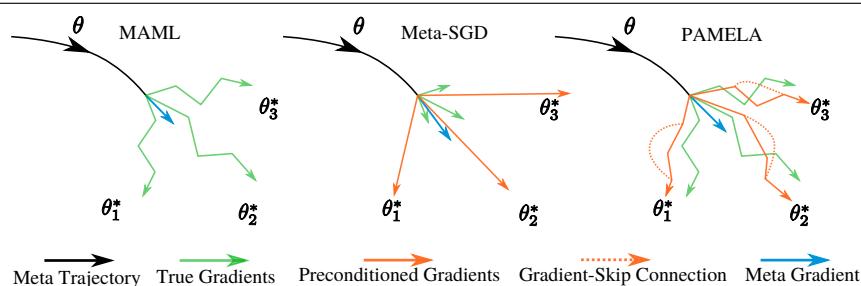
MAML、Meta-SGD 和 PAMELA 的内循环优化路径对比。MAML 遵循真实梯度，Meta-SGD 使用单个预处理步骤，而 PAMELA 采用多个具有跳跃连接的独特预处理步骤。

图 1: 内循环优化策略。MAML (左) 沿标准梯度方向进行多步更新；Meta-SGD (中) 在元学习得到的方向上进行单步更新；PAMELA (右) 执行多步更新，每步都有独特的元学习方向，并通过“梯度跳跃”连接共享过往更新信息。

在 PAMELA 中，内循环的每一步都有自身的学习行为。它不再依赖静态的更新规则，而是动态地学习如何学习。

形式上，PAMELA 最小化适应后的验证损失:

\[ \underbrace{\min_{\boldsymbol{\theta}, \boldsymbol{\Phi}} \mathbb{E}_{\mathcal{T} \sim P(\mathcal{T})} \left[ \mathcal{L}_{\mathcal{D}_{val}}\left( f_{\underbrace{\mathbf{F}_{\boldsymbol{\Phi}}(\boldsymbol{\theta})}_{inner-loop}} \right) \right]}_{outer-loop} \]

函数 \( \mathbf{F}_{\Phi} \) 表示 PAMELA 的内循环优化器，由元参数 \( \Phi = \{Q, P^w\} \) 参数化。这些参数使得学习过程更加灵活并具备上下文感知性。

1. 逐步学习方向: \( Q \)

第一个创新是为内循环的每一步 \( j \) 学习独立的预处理矩阵 \( Q_j \)。与 Meta-SGD 的单一全局预处理矩阵不同，PAMELA 为不同步学习 \( Q_0, Q_1, Q_2, \dots \)。

这使元学习器能够随时间调整更新的幅度与方向。早期步骤可能在 \( Q_0 \) 的引导下进行较大的探索性移动，而后期步骤则在 \( Q_4 \) 的引导下进行更小、更精细的调整。通过这种方式，PAMELA 捕捉了学习速率在任务适应过程中的动态变化。

2. 梯度跳跃连接: \( P^w \)

第二项创新引入了来自过去的上下文信息。PAMELA 使用梯度跳跃连接 , 将当前更新与若干步之前的参数状态混合。

不同于 ResNet 的跳跃连接 (连接的是激活层) ，PAMELA 的跳跃存在于参数空间中。它通过融合当前更新与过往参数信息，帮助模型保持稳定并避免过拟合。

更新规则结合两种机制:

\[ \boldsymbol{\theta}_{j+1} = \begin{cases} \boldsymbol{\theta}_j - \boldsymbol{Q}_j \circ \nabla_{\boldsymbol{\theta}_j} \mathcal{L}_{\mathcal{D}_{tr}}(f_{\boldsymbol{\theta}_j}) & \text{if } (j \text{ mod } w) \neq 0, \\ (1 - P_j^w) \circ \{\boldsymbol{\theta}_j - \boldsymbol{Q}_j \circ \nabla_{\boldsymbol{\theta}_j} \mathcal{L}_{\mathcal{D}_{tr}}(f_{\boldsymbol{\theta}_j})\} + P_j^w \circ \boldsymbol{\theta}_{j-w} & \text{else.} \end{cases} \]

其中 \( \circ \) 表示逐元素乘法。当条件 \((j \text{ mod } w) \neq 0\) 不成立时，PAMELA 使用可学习系数 \( P_j^w \) 在当前与前序梯度之间交织信息，使模型能够记住此前适应的上下文。

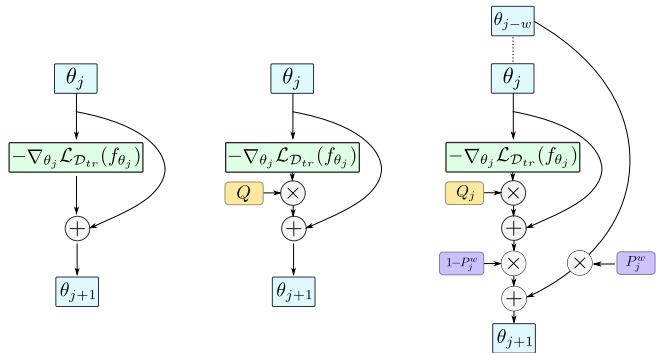
MAML、Meta-SGD 和 PAMELA 内循环更新规则的示意图。

图 2: 内循环更新对比。MAML (左) 应用直接梯度更新；Meta-SGD (中) 引入单一预处理矩阵 \( Q \)；PAMELA (右) 在每步学习独特的 \( Q_j \)，并通过 \( P_j^w \) 混合参数，以实现更加丰富的自适应动态。

外循环: 学习路径发现者

完成内循环更新后，PAMELA 在验证集上评估适应后的模型 \( \theta_n \)。其产生的验证损失通过所有内循环步骤反向传播，不仅更新初始化参数 \( \theta \)，还更新各个 \( Q_j \) 和 \( P_j^w \):

[ {\boldsymbol{\theta}^{new}, \boldsymbol{\Phi}^{new}} = {\boldsymbol{\theta}, \boldsymbol{\Phi}}

  • \boldsymbol{\beta} \nabla_{{\boldsymbol{\theta}, \boldsymbol{\Phi}}} \sum_{k=1}^{K} \mathcal{L}{\mathcal{D}{val}^k}(f_{\boldsymbol{\theta}_n^k}) ]

该外循环确保 PAMELA 不仅学会从哪里开始，还学会如何在路径上最优地学习。

PAMELA 的实证检验

理论之外——PAMELA 的复杂设计是否真的带来性能提升？答案是肯定的。研究团队在多个标准少样本学习基准上进行了广泛实验。

少样本图像分类

研究团队在三个常用数据集上评估了 PAMELA: miniImageNet、CIFAR-FS 和 tieredImageNet 。

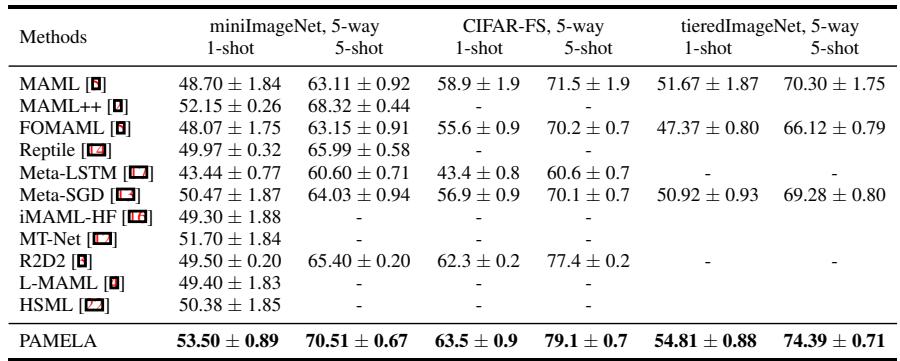
在 miniImageNet、CIFAR-FS 和 tieredImageNet 上的少样本分类结果表。PAMELA 在 1-shot 和 5-shot 设置下均持续优于其他方法。

图 3: 少样本分类任务准确率。PAMELA 在多个基准中均取得一致、领先的结果。

在所有数据集上，PAMELA 的表现均超越了 MAML、MAML++ 和 Meta-SGD 等方法。在 miniImageNet 5-way 5-shot 任务中，PAMELA 达到 70.51% 的准确率，远高于 MAML 的基线 \(63.11\%\)。在 1-shot 以及 CIFAR-FS 和 tieredImageNet 任务上也呈现相同趋势。学习适应路径显然带来了更强的泛化能力。

少样本回归

为了检验分类之外的适应能力，作者将 PAMELA 用于拟合不同振幅、频率和相位的正弦波。每个任务仅提供少量数据点。

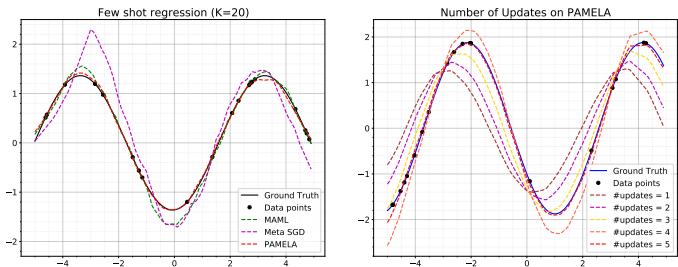
正弦波回归任务结果。左: PAMELA 比 MAML 和 Meta-SGD 拟合真实曲线更好；中: 曲线随更新次数改善；右: PAMELA 获得最低均方误差。

图 4: 正弦波回归结果。PAMELA 生成的拟合曲线更加平滑、精确，并持续获得最低的均方误差。

结果令人印象深刻。PAMELA 的曲线几乎完美契合真实曲线，并在连续更新中纠正过冲，展现出其学习轨迹能够实现自我修正的优化行为。

PAMELA 为何有效？来自消融实验的洞察

为理解每一组件的作用，研究者进行了消融实验，对 \( Q \) 与 \( P^w \) 分别进行剖析。

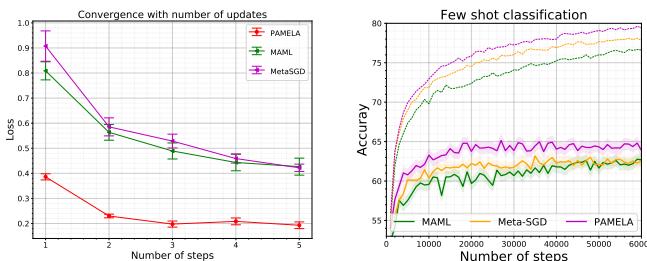
PAMELA 性能及组件贡献对比分析。左: 内循环损失方差更低；中: 测试准确率提升更快；右: 消融实验表格分解了 Q 与 P^w 的贡献。

图 5: PAMELA 的训练动态与消融研究。步级预处理 (\(Q\)) 与跳跃连接 (\(P^w\)) 同样关键。完整模型在极小复杂度增加下实现了最高准确率。

关键发现如下:

  1. MAML 基础版: 准确率约为 63.11%。
  2. MAML + 单一 \( Q \): 扩展到多步后性能下降至 62.71%。
  3. MAML + 多步 \( Q_j \): 动态逐步 \( Q \) 提升至 66.18%。
  4. MAML + \( P^w \): 仅启用梯度跳跃连接即可使准确率提升至 69.71%。
  5. 完整 PAMELA (Q + P^w): 二者结合取得最佳结果——70.51%。

这些结果证明 PAMELA 的创新存在协同效应: 步级动态与历史上下文融合共同构建了更稳健、更具泛化能力的元学习器。

模型复杂度也保持合理:

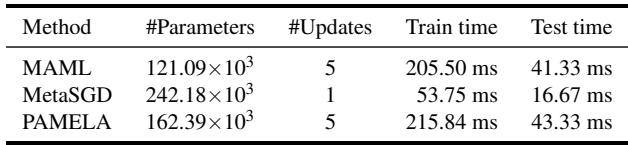
MAML、Meta-SGD 和 PAMELA 的参数量与计算时间对比。

表 1: 复杂度对比。PAMELA 仅增加适度的参数与极少的额外计算，使性能提升具备可行性。

PAMELA 比 MAML 多约 34% 的参数，但训练与推理时间几乎相同——这是为了持续准确率提升所付出的微小代价。

结论: 路径即目标

PAMELA 标志着元学习理念的重要进化。它将焦点从单纯寻找“良好初始化”转向学习整个适应路径。通过结合步级梯度预处理与上下文保留的梯度跳跃连接 , PAMELA 建模了学习行为在时间上的动态变化。

这种方法带来:

  • 动态学习行为: 在每一内循环步骤中调整学习率与方向。
  • 上下文自适应能力: 将过去的知识融入当前学习以增强稳定性。
  • 更快收敛与更高准确率: 已在多个数据集上得到验证。

简而言之，PAMELA 不仅学习从何处开始——还学习如何前进。随着元学习研究的不断深入，PAMELA 表明，理解适应过程本身或许能开启下一代真正类人的学习系统。