从不存在的人物的超写实肖像，到仅凭一句话绘出的史诗级风景，扩散模型为当今许多最令人惊叹的生成系统提供了动力。短短几年间，它们已从一个前景广阔的理论，发展成为图像、视频、3D、音频乃至分子设计等领域中最先进系统的核心支柱。

本文是对综述文章《扩散模型: 方法与应用综合综述》 (Yang 等，2023) 的导览。我的目标是带您从核心直觉出发，了解其技术基础，再穿越主要的研究方向以及最令人振奋的应用。在必要时，我会引用论文中的图示来帮助说明。

如果您是正在努力理解相关文献的学生或研究者，可将本文视作一枚指南针: 它描绘了知识地图、主要的研究路线以及那些重要的地标。

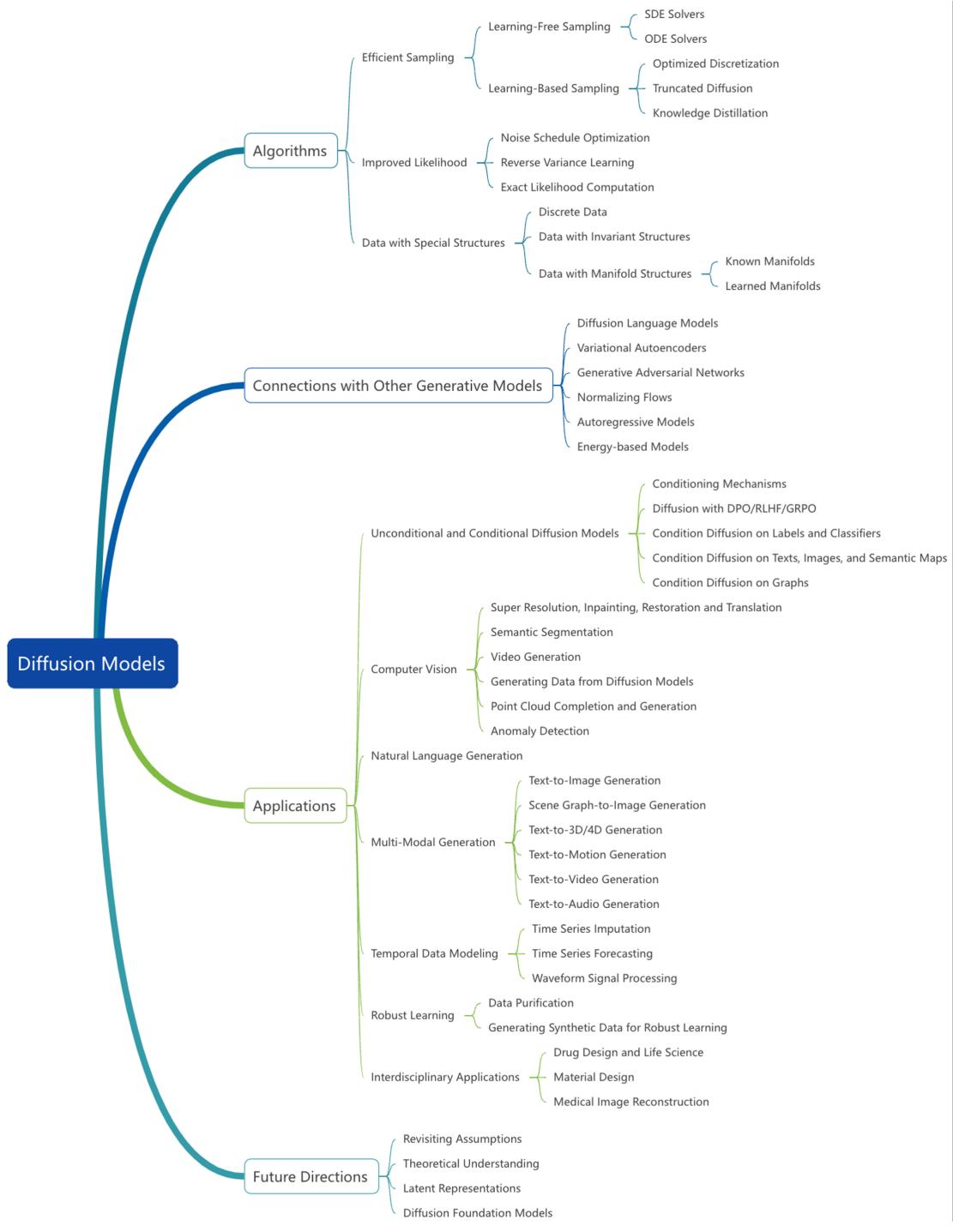
一张思维导图，展示了扩散模型的分类，涵盖算法、应用、与其他生成模型的联系及未来方向。

图 1 — 综述涵盖的扩散模型研究的高层级分类: 核心算法变体、高效采样方法、似然改进、领域自适应、与其他生成模型家族的联系、应用及未来方向。

目录

  • 基础——强大模型背后的两个简单思想
  • 三种数学视角: DDPM、分数匹配与随机微分方程 (SDE)
  • 加速扩散: 采样方法
  • 收紧似然与原则性训练
  • 扩散模型在非图像领域与结构数据中的适配
  • 扩散模型与 VAE、GAN、流模型、自回归模型、能量模型及大语言模型 (LLM) 的联系
  • 应用: 视觉、多模态、音频、时间序列、分子与医学
  • 展望: 未来研究方向
  • 总结

基础——破坏 + 重建

扩散模型的核心思想包含两个过程:

  1. 一个固定的、前向过程: 逐步破坏 (添加噪声至) 真实数据，直到其变为一种简单且易于处理的分布 (通常是高斯噪声) 。
  2. 一个可学习的、反向过程: 从噪声开始，逐步去噪，直至恢复出一个数据样本。

这种“先破坏后重建”的策略，把密度估计转化为一系列局部去噪问题。直观上，每一步去噪只需进行一次微小的局部修正——这是神经网络能够稳定学习的任务。

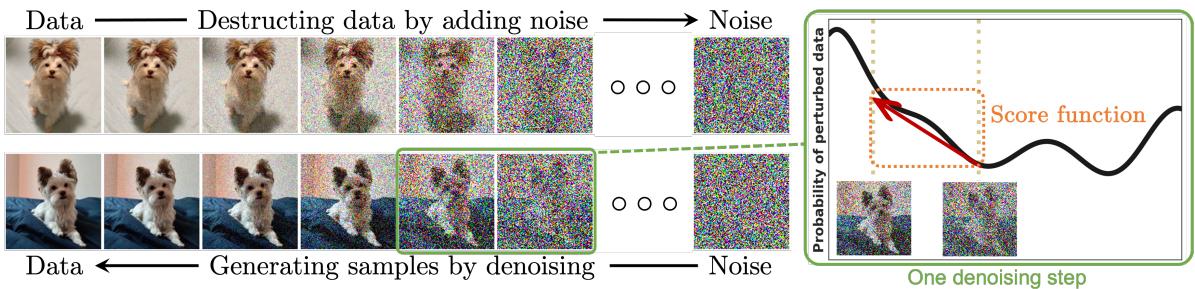
一张示意图，展示了扩散模型的两步过程: 通过添加噪声破坏数据，再通过学习反向去噪过程来生成样本。

图 2 — 前向过程缓慢地向一个干净样本注入高斯噪声，直到其看起来像随机噪声；训练好的反向过程则一步步移除噪声以生成新样本。右图可视化了分数方向: 在每个噪声水平上，分数都指向数据密度更高的区域。

接下来，我们将通过文献中三种主流的形式化方法来精确定义这些思想。

三种在本质上等价的数学视角

该综述将扩散模型从三个互补的角度加以阐释。每个角度都带来了独特的直觉和实用算法。

1) 去噪扩散概率模型 (DDPM)

DDPM 建立了两个离散的马尔可夫链:

  • 前向链 q(x_t | x_{t-1}) —— 一个简单的、固定的高斯噪声添加序列，最终使数据接近高斯噪声。
  • 反向链 p_theta(x_{t-1} | x_t) —— 可学习的；由神经网络参数化每个反向核的均值和 (可选的) 方差。

一个常见的前向核定义为:

\[ q(x_t \mid x_{t-1}) = \mathcal{N}\big(x_t; \sqrt{1-\beta_t}\,x_{t-1},\; \beta_t I\big), \]

其中噪声调度 \(\{\beta_t\}\) 控制每一步添加的噪声量。一个方便的性质是，可以直接从 \(x_0\) 采样出任意时刻 \(t\) 的 \(x_t\):

\[ x_t = \sqrt{\bar\alpha_t}\,x_0 + \sqrt{1-\bar\alpha_t}\,\epsilon,\quad \epsilon\sim\mathcal{N}(0,I), \]

其中 \(\bar\alpha_t=\prod_{s=1}^t (1-\beta_s)\)。

训练过程中最大化数据对数似然的变分下界 (VLB) 。Ho 等人提出的重参数化方法导出一个简单有效的训练目标: 根据 \(x_t\) 和 \(t\) 来预测注入的噪声 \(\epsilon\)。其损失函数为:

\[ \mathbb{E}_{t,x_0,\epsilon}\big[\lambda(t)\,\|\epsilon - \epsilon_\theta(x_t,t)\|^2\big], \]

该损失函数数值稳定、经验效果良好。

备注:

  • DDPM 概念简洁，易于实现。
  • 采样过程较慢，通常需要多次网络评估 (数百到数千步) ，因此催生了后续的快速采样研究。

2) 基于分数的生成模型 (SGM)

分数模型通过学习带噪数据分布的分数函数来解决问题:

\[ s_\theta(x,t)\approx\nabla_x\log q_t(x), \]

其中 \(q_t\) 为添加了方差 \(\sigma_t^2\) 的高斯噪声后 \(x_t\) 的密度。得到多个噪声层次下的分数估计后，可通过朗之万动力学或其他基于分数的采样器进行采样: 沿着分数方向迈小步，并添加少量高斯噪声以鼓励探索。

其训练目标为多尺度的去噪分数匹配损失。经过代数变换后，在适当参数化下与 DDPM 损失等价。这种等价是核心——DDPM 和 SGM 是同一去噪任务的不同视角。

3) 连续极限: 分数 SDE 与概率流 ODE

DDPM 与 SGM 均可视作连续时间随机微分方程 (SDE) 的离散化:

\[ d x = f(x,t)\,dt + g(t)\,d w_t, \]

其中 \(w_t\) 是布朗运动。前向扩散是一个把数据逐渐模糊成噪声的 SDE。根据 Anderson 定理，逆时 SDE 的漂移项包含分数 \(\nabla_x\log q_t(x)\)。若能估计该分数，即可求解逆时 SDE 生成样本。

还可以定义一个确定性常微分方程——概率流 ODE，其轨迹与 SDE 具有相同的边缘分布。求解该 ODE 可获得确定性采样方式，并能与连续归一化流直接关联，实现对数密度的精确 (或紧界) 计算，但需付出 ODE 求解代价。

这些视角的重要性:

  • DDPM 方便、易训练；
  • SGM 提供分数场的直觉并允许 MCMC 采样；
  • 分数 SDE 与概率流 ODE 统一了两者框架，拓展了似然评估与确定性采样的新途径。

快速采样: 让扩散模型实用化

扩散模型最大的实际问题是采样时间。早期模型需数百或数千个顺序去噪步骤。该综述将相关进展分为两类: 无需学习的数值求解器与基于学习的加速方法 。

无需学习的求解器: 更聪明的离散化

此类方法保留预训练模型，专注于逆时 SDE 或概率流 ODE 的高效数值求解。

  • ODE 求解器 : DDIM 提出确定性采样器，对应于概率流 ODE 的特殊离散化。后续方法 (Heun 方法、DPM-Solver、扩散指数积分器等) 利用高阶数值积分或 ODE 的半线性结构，在保持样本质量的前提下显著减少采样步数 (常至 10–50 步) 。
  • SDE 求解器与预测-校正方案 : 随机采样器可带来更好混合与保真度。预测-校正方案将粗略 SDE 或 ODE 步骤 (预测器) 与分数引导的 MCMC 微调 (校正器) 结合。自适应步长与朗之万“扰动”步骤也提升了效率与样本质量。

权衡: 确定性 ODE 求解器更快但可能稍损多样性；随机求解器质量更优但需更多步骤。

基于学习的加速

通过训练附加模块加速采样:

  • 知识蒸馏 : 渐进式蒸馏训练一个快速“学生”来模仿多步“教师”；每阶段可将采样步数减半。
  • 优化离散化 : 对已训练模型，可搜索最优离散时间点集合以最大化样本质量。已尝试可微搜索与动态规划方法。
  • 截断扩散 : 提前停止前向加噪，从非高斯但结构化的分布开始反向生成，该分布由更快生成器 (如 VAE 或 GAN) 建模。此方案缩短扩散轨迹但需联合另一个模型。

实际效果: 现代系统可在 10–50 次网络调用内生成高质量图像——在充分优化工程条件下，甚至接近实时。

提升似然: 从启发式到原则性目标

扩散模型训练常以 VLB 为目标，但该下界可能较松。综述将提升似然的研究归为三类:

  1. 噪声调度优化 : \(\beta_t\) 的选择影响样本质量与似然。iDDPM、VDM 等工作通过学习连续时间调度 (以单调神经网络参数化) 来收紧 VLB。
  2. 反向方差学习 : 早期 DDPM 使用固定反向方差；通过学习反向方差或从分数估计推导解析最优 (Analytic-DPM) 可改善 VLB 并提高似然估计。
  3. 精确似然 / ScoreFlows : 在连续 SDE 框架中，可直接针对逆时 SDE 或概率流 ODE 生成样本的似然建立界与变分目标。ScoreFlows 等方法借此实现更严格的最大似然训练与更准确的对数密度估计，代价是更高的计算负荷。

重要性: 更紧的似然可使扩散模型成为真正的概率模型，而不只是采样器。对异常检测或需校准密度的科学任务尤为关键。

结构化与非标准数据的扩散模型

标准扩散模型假设数据在连续欧几里得空间中，并使用高斯噪声。许多领域并不符合此设定。综述介绍了以下推广方法:

离散数据 (文本、类别符号)

高斯噪声不适用于离散空间。解决方案包括:

  • 在离散状态空间上使用随机游走或掩码破坏过程 (多项式扩散、吸收态) ；
  • 具体分数匹配 (Concrete score matching) : 针对离散变量的有限差分近似；
  • 利用连续时间马尔可夫链形式，使离散扩散可在连续时间运行并实现高效采样。

这些方法使扩散式生成可应用于文本、符号序列及其他离散模态。

具有对称或不变性的结构数据 (图、点云、分子)

许多数据具备对称性 (图的置换不变性、分子的旋转/平移不变性) ，模型需具备等变性:

  • 对图数据，采用置换等变图神经网络 (GNN) ，使反向核保留图生成的置换不变性；
  • 对 3D 分子坐标，构建 E(3)/SE(3) 等变的分数网络，使去噪对旋转/平移共变，从而保持物理属性并提高生成质量。

流形数据 (球面气候数据、受约束域)

若数据位于已知流形，可:

  • 在黎曼流形上定义 SDE 并将分数匹配方法适配其几何；
  • 使用外在或内在构造 (黎曼分数模型、测地随机游走) 直接在流形上扩散。

若流形未知，则可采用隐空间扩散: 训练编码器 (如自编码器/VAE) 将数据映射到低维隐空间，并在此空间中进行扩散 (隐空间扩散模型 LDM) 。该方法训练与采样更高效，是大型系统 (如 Stable Diffusion) 的基础。

扩散模型与其他生成范式——互补优势

扩散模型并未取代其他生成范式，而是与它们相互补充。综述给出了多种重要联系。

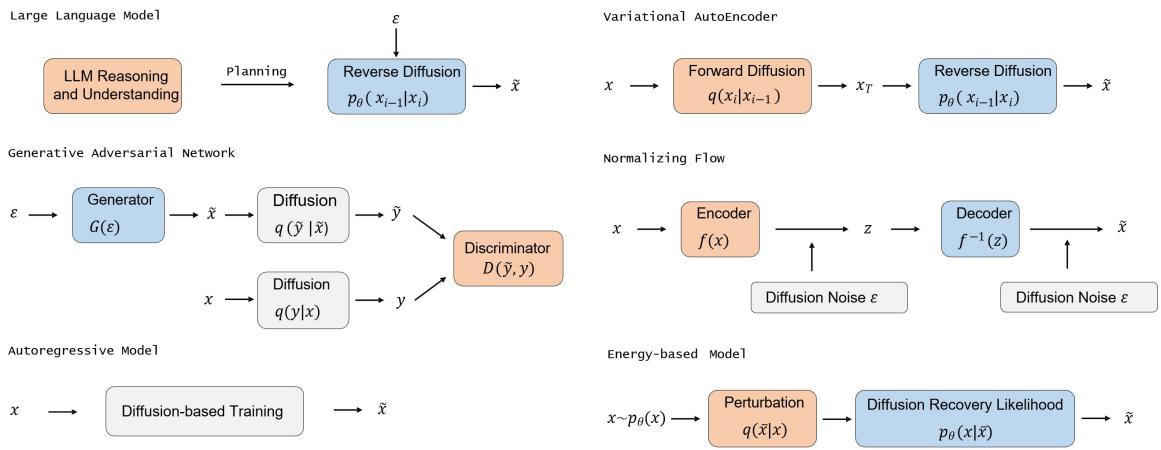
一张示意图说明扩散模型如何与大语言模型、VAE、GAN、归一化流、自回归模型及能量模型集成。

图 3 — 扩散组件如何融入不同生成架构: LLM 可作为局部扩散的规划器或控制器；VAE 提供高效扩散的隐空间 (LDM) ；GAN 可建模较大步长的去噪或稳定训练；流模型和 CNF 由概率流 ODE 联系；自回归与能量模型在理论上与分数匹配相关。

亮点:

  • VAE : DDPM 与无限深层次的 VAE 紧密相关；结合自编码器与扩散 (隐空间扩散) 将极大提升效率。
  • GAN : GAN 可用于建模大步去噪或稳定训练；混合扩散-GAN 模型试图兼顾高保真与生成速度。
  • 归一化流/CNF : 概率流 ODE 将扩散与连续流连接；扩散模型可在不需严格双射条件下建模复杂分布。
  • 自回归模型 : 部分扩散形式近似自回归分解；混合自回归扩散模型权衡并行性与密度估计。
  • 能量模型 (EBM) : 分数匹配与 EBM 在理论上接近；扩散恢复似然可使训练 EBM 序列更可行。
  • LLM : 最新趋势将 LLM 的世界知识与规划能力结合扩散采样，用于视觉生成与编辑。LLM 负责解析复杂提示、规划构图并提供结构指导，实现更强的组合式生成。

这些结合产生了更可控、更具组合性且功能更强的系统。

应用——扩散模型的闪耀之处

扩散模型已在多个领域取得突破。以下是最具影响力的应用与实例。

计算机视觉: 生成、修复与编辑

  • 高保真无条件与条件图像合成 (DDPM, LDM) : Imagen、GLIDE、Stable Diffusion 等模型利用文本或其他输入条件生成惊艳图像。
  • 超分辨率、补全、恢复: SR3、RePaint、DDRM、Palette、ConPreDiff 将恢复建模为条件去噪任务，达到了极高感知质量。
  • 语义分割与表征学习: 扩散预训练产生的特征对高效标注任务很有帮助。
  • 视频生成: 时空扩散结构和级联模型可生成短视频，时间一致性日益提升。

ConPreDiff 模型的图像补全结果对比，展示原图、遮挡图和模型重建输出。

图 4 — ConPreDiff 图像补全示例: 基于部分输入与上下文条件生成高质量重建结果。

EditWorld 与其他模型 (如 InstructPix2Pix、MagicBrush) 生成的图像编辑结果对比，展示其处理复杂世界知识指令的能力。

图 5 — EditWorld 合成大规模遵循指令的编辑数据集，帮助改进下游图像编辑模型。

多模态: 文本→图像、文本→视频、文本→3D 等

  • 文生图 : Stable Diffusion、DALLE‑2 (unCLIP) 、Imagen 等通过文本嵌入 (CLIP/T5) 条件扩散，结合无分类器引导、交叉注意力与布局控制。
  • 组合与可控生成 : 使用 LLM 作为规划器的方法 (如 RPG、IterComp) 将复杂提示拆分为区域或子提示，提升组合性。
  • 文生视频 : 级联或分解扩散模型 (Imagen Video、Make‑A‑Video) 将图像先验扩展到时间域。
  • 文生 3D 资产生成 : DreamFusion、Magic3D 等采用 2D 扩散先验优化 3D 表示 (NeRF、隐式函数) 。
  • 音频与语音 : WaveGrad、DiffWave、Grad‑TTS 使用分数模型与扩散解码器进行波形合成及文本到语音转换。

一个网格图比较 LDM、Imagen 与 ContextDiff 在不同文本提示下的文生图表现。

图 6 — 不同扩散骨干架构的文生图定性比较，展示条件与上下文建模对保真度与对齐度的影响。

时间序列与波形建模

  • 插补与预测 : CSDI、SSSD 及检索增强扩散方法 (RATD) 使用条件分数模型提供有原则的不确定性与数据一致插补。
  • 波形生成 : WaveGrad、DiffWave 实现高质量音频生成，在步数与保真度间取得平衡。

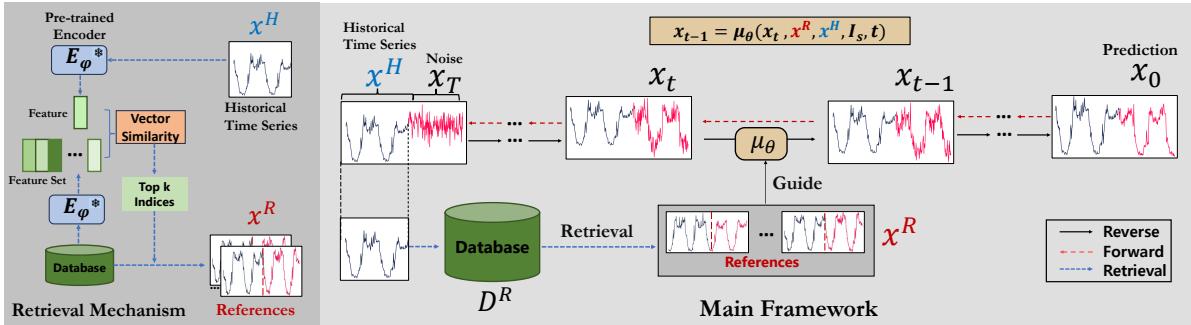
RATD 时间序列预测框架概览，展示通过检索相关历史参考增强扩散模型。

图 7 — 检索增强的时间序列扩散预测: 检索相似历史上下文，并据此条件去噪，以获得更佳预测。

科学与跨学科应用

  • 分子与蛋白质设计 : GeoDiff、Torsional Diffusion、ConfGF、IPDiff 利用等变模型和蛋白质条件先验生成分子构象与靶向配体。
  • 材料与晶体生成 : CDVAE 等模型可生成周期性晶体结构。
  • 医学影像 : 基于分数的重建方法通过结合测量前向模型与学习先验解决逆问题 (MRI、CT) 。

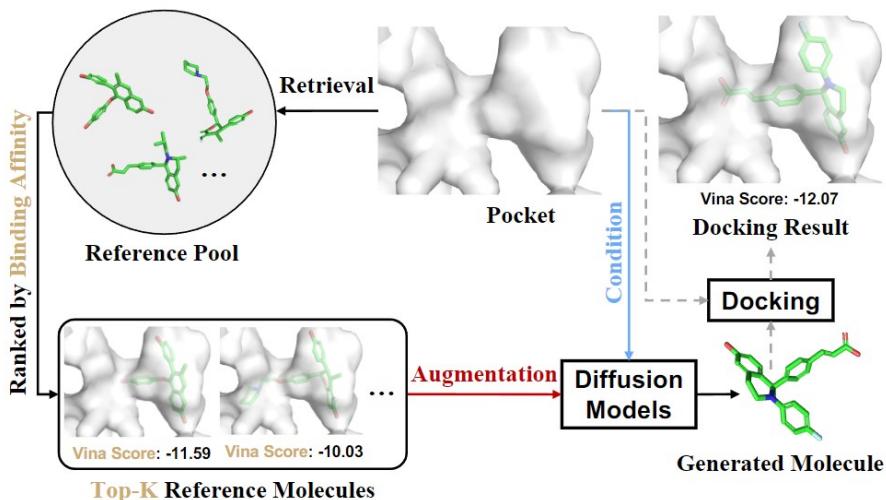
IRDiff 模型示意图，展示利用检索增强方法指导基于扩散的 3D 分子生成，用于药物设计。

图 8 — 结构导向药物设计中的检索增强与交互感知扩散: 检索提供结合基序参考，扩散模型生成候选配体并经对接评估。

实用指南——何时使用扩散模型

  • 当需要高质量、高多样性样本及稳定训练时，选择扩散模型 (比 GAN 更鲁棒) 。
  • 当计算或内存受限时，优先采用隐空间扩散 (LDM) ，在压缩隐空间训练重型模型。
  • 若生产环境需快速采样，可采用蒸馏或 DPM‑Solver/指数积分器，通常能实现 10–20 步采样。
  • 对结构化数据 (图、分子、点云) 应选用等变结构和领域感知破坏过程。
  • 若校准似然尤为重要，考虑 ScoreFlows 或似然感知训练目标。

开放问题与未来方向

综述指出了几项重要且令人兴奋的研究前沿:

  • 重新审视假设 : 能否设计比传统长扩散更高效的有限时间桥 (如薛定谔桥、最优传输) ？
  • 理论理解 : 扩散模型为何能生成如此高质量样本？时间表、参数化与结构的最优设计是什么？
  • 隐空间与紧凑表示 : 如何让扩散模型学习有意义、低维、对下游任务有用的隐变量？
  • 基础模型与 AIGC : 扩散能否像 LLM 一样成为基础技术？融合 LLM 与扩散的多模态、多任务规模化前景如何？
  • 效率与保真度权衡 : 如何在不牺牲质量的情况下实现极快采样，仍是工程与理论前沿。

结语

扩散模型融合了优雅的理论与卓越的实践。其核心思想——学习去噪逐步被破坏的数据——虽简单，却带来了深远影响。短短几年间，扩散方法从概念验证发展为驱动文本生成图像艺术、科学设计工具与鲁棒生成先验的核心引擎。

这篇综述 (Yang 等，2023) 是一份极佳的路线图: 它贯通了数学基础，系统梳理了采样与似然的快速进展，并总结了特定领域的适配与应用。对所有研究或应用现代生成模型的人而言，扩散模型如今已成为工具箱中的必备利器。

若想进一步深入，建议直接阅读该综述——其中包含详尽的分类、丰富的技术推导及参考文献，可快速定位原始研究。

祝阅读愉快——愿你的采样器更快，样本更美。