如果你曾尝试逆向工程一个神经网络的行为，你很可能注意到一个让人沮丧的事实: 神经元很“乱”。一些神经元表现得像干净的检测器——“这里是曲线”、“那里是狗鼻子”——而许多其他神经元则是多语义的 (polysemantic) : 它们会对看似毫无关联的事物作出响应。为什么会这样？Anthropic 于 2022 年发表的论文《叠加的玩具模型》 (Toy Models of Superposition) 给出了一个简明的解释: 在许多情况下，网络试图表示的稀疏特征远超其神经元数量，因此它们将多个特征“打包” (或“叠加”) 到重叠的激活模式中。这种打包带来了多语义神经元、结构化的干扰，以及 (令人意外的) 美丽几何结构。

本文将带你走过那篇论文的思想与实验。我们将从第一性原理建立直觉，考察玩具实验，并探讨由此产生的结果: 相变、几何结构 (多胞体！) 、叠加状态下的计算，以及与对抗性脆弱性之间的联系。我们将保持解释的具体性，让研究人员和实践者都能获得关于模型内部机制的可行洞察。

目录

  • 背景: 特征、方向与特权基
  • 演示叠加: 玩具自编码器实验
  • 表示中的相变
  • 叠加的几何学
  • 叠加状态下的计算 (abs(x) 实验)
  • 与对抗性脆弱性的联系
  • 对可解释性和安全性的影响
  • “解决”或缓解叠加的策略
  • 局限性、开放问题与总结

背景: 特征、方向与特权基

要推理叠加现象，我们需要明确的词汇。

  • 特征 (Feature) : 粗略地说是输入的一种可解释属性 (如耷拉的耳朵、某个特定的词元等) 。论文采用的定义是务实的: 一个足够大的模型会为该属性分配专用神经元。
  • 方向性/线性表示 (Directional / linear representation) : 假设特征被表示为激活空间中的方向。如果特征 \(f_1, f_2, \dots\) 有标量激活值 \(x_{f_1}, x_{f_2}, \dots\) 和方向 \(W_{f_1}, W_{f_2}, \dots\)，则层激活近似为 \[ x_{f_1} W_{f_1} + x_{f_2} W_{f_2} + \dots \] 这并不是说特征是输入的线性函数——只是说从特征到激活的映射近似线性。
  • 特权基与非特权基 (Privileged vs non‑privileged bases) : 当某些架构设计使基方向变得特殊时，该基被称为特权基 (例如，ReLU 这样的逐元素非线性激励会鼓励特征与神经元方向对齐) 。词嵌入和残差流通常是非特权基 (具有旋转对称性) ，而带 ReLU 的 MLP 层则属于特权基。

为什么这些概念重要？如果基是特权的且特征与基方向对齐，神经元会更容易被解释；而在非特权基中，特征可能分布在任意方向，我们就需要特征分析方法来识别它们。叠加现象即便在存在特权基的情况下也会使特征偏离对齐，这也解释了为什么多语义神经元如此常见。

一个来自高维几何与压缩感知的重要直觉是: 虽然在 \(\mathbb{R}^m\) 中只能有 \(m\) 个完全正交的向量，但可以存在指数级数量的近乎正交向量。如果特征是稀疏的 (激活很少) ，可以容忍这些近乎正交方向之间的轻微串扰 (干扰) ，并在大多数情况下成功恢复出当前激活的特征。这个权衡正是叠加的核心。

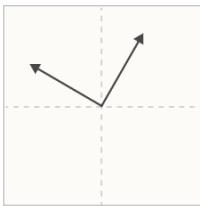
当我们观察到特征与神经元的基方向不对齐时，就称之为多语义性。

当特征没有与“一特征一神经元”的整洁基对齐时，我们观察到的就是多语义性。在高维空间中，许多近乎正交的方向使得我们能够将更多特征压缩进更少的神经元。

演示叠加: 玩具自编码器实验

作者首先研究一个简单且具体的问题: 神经网络是否能够模糊地表示比其神经元数量更多的特征？他们通过一个高度受控的合成实验来测试这一点。

实验设置概要:

  • 输入向量 \(x \in \mathbb{R}^n\)。每个坐标 \(x_i\) 是一个“特征”，每个特征具有:
  • 稀疏性 \(S_i\) (为零的概率；通常使用统一 \(S\)) ，
  • 重要性 \(I_i\) (训练损失中的权重) ，
  • 若非零，\(x_i\) 从 \([0,1]\) (或 \([-1,1]\)) 中均匀采样。
  • 两类模型:
  • 线性模型: \(h = W x,\; x' = W^\top h + b\)，行为类似 PCA 自编码器。
  • ReLU 输出模型: \(h = W x,\; x' = \mathrm{ReLU}(W^\top h + b)\)。仅输出层有 ReLU。
  • 损失函数: 加权均方误差 \[ L = \mathbb{E}_x \sum_i I_i (x_i - x'_i)^2. \]
  • 关键诊断指标:
  • 列向量 \(W_i\): 输入特征的嵌入方式
  • 格拉姆矩阵 \(W^\top W\): 展示特征间的重叠情况
  • 范数 \(\|W_i\|\): 特征是否被有效表示
  • “叠加度量”: 其他特征在 \(\hat W_i\) 上的投影量

实验结果:

  • 线性模型的行为类似 PCA: 为前 \(m\) 个主要特征提供彼此正交的方向，忽略其余特征。
  • ReLU 输出模型在特征密集时的表现与线性模型相似。但当特征变得稀疏，ReLU 模型可以通过近乎正交的方向来表示超过 \(m\) 个特征。起初采用对跖对 (方向互为相反) ，随后随着稀疏性增加出现更复杂的打包。

ReLU 的关键作用:

ReLU 对正负干扰的处理是非对称的。当干扰使得点积为负而被 ReLU 截断为零时，这种干扰对损失不会造成影响，从而成为“免费干扰”。这种非对称性使得模型能在有限维度中打包更多特征: 负干扰可接受，正干扰代价高。而偏置项则可通过平移阈值把部分轻微的正干扰转化为有效的负干扰。

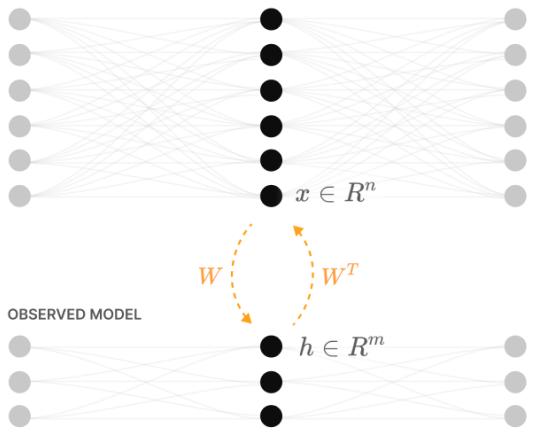
线性模型与 ReLU 输出模型在不同稀疏度下的对比。

左列是线性模型的 \(W^\top W\) 和特征范数 (它选择前 m 个特征) ；右列为 ReLU 模型，在密集区与线性模型相似，随后随着稀疏度上升逐渐进入叠加状态打包更多特征。

这个实验明确展示了: 叠加并非纯理论猜测——即便在非常小的 ReLU 网络上，只要稀疏特征出现且对损失有利，模型就会主动打包比神经元数量更多的特征。

表示中的相变

一个显著的发现是，单个特征进入叠加状态的过程并非渐变的，而更像一个相变。对于某个特征，训练后的结果通常落入三种状态:

  • 未被表示；
  • 以专用 (正交) 维度表示；
  • 在叠加中表示 (共享部分维度) 。

作者用微型解析示例分离这一现象。考虑 \(n=2\) 个特征、\(m=1\) 个隐藏维度，仅有几种自然解:

  • \(W=[1,0]\): 只表示特征 1 (特征 2 忽略)
  • \(W=[0,1]\): 只表示特征 2
  • \(W=[1,-1]\): 对跖式地同时表示两个特征 (叠加)

当改变两个条件——特征 2 的稀疏性与相对重要性——可得清晰的相图。在某些区域，叠加解最优；其他区域则更适合忽略额外特征或牺牲另一个特征为其专用维度。这些边界清晰且陡峭。

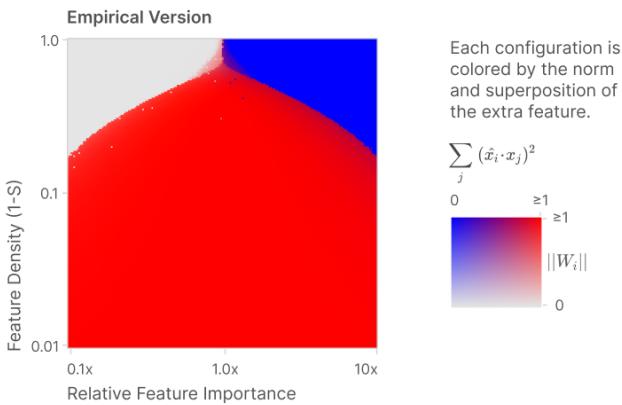
n=2, m=1 设置下的相图: 经验 (左) 与理论 (右) 。

存储两个特征到一个维度的经验 (左) 与理论 (右) 相图。坐标轴为特征密度 (\(1-S\)) 与相对重要性。红色区域表示叠加 (对跖解) 最优。

进一步分析至 \(n=3, m=2\) 等更复杂设置时，理论与实验结果仍完全匹配。结论: 一个特征是否进入叠加状态由稀疏性与重要性之间的尖锐交互决定。

叠加的几何学

一旦出现叠加，学习到的嵌入并非随机分布，而是形成高度结构化的几何构型。在特征重要性和稀疏性均匀的情况下，最优排列对应于熟悉的均匀多胞体: 二角形 (对跖对) 、三角形、四面体、五边形、方形反棱柱等。这与汤姆逊问题 (球面上互斥电荷的优化分布) 高度类似: 模型通过散开特征向量来最小化干扰，仿佛在最小化静电势能。

关键定义:

  • 有效学习的特征数: \(\|W\|_F^2 = \sum_i \|W_i\|^2\)。若 \(\|W_i\|^2 \approx 1\) 被表示、\(\approx 0\) 被忽略，则该值近似表示特征数。
  • 特征维度: \[ D_i = \frac{\|W_i\|^2}{\sum_j (\hat W_i \cdot W_j)^2}. \] 表示特征 \(i\) 占据隐藏维度的比例。例如在对跖对中，每个特征 \(D=1/2\)。这些 \(D_i\) 结果倾向在表示特定多胞体顶点度数的有理分数聚集。

粘性分数与多胞体:

绘制 \(D_i\) 随稀疏性变化时，数据点常聚集于水平线，表明系统偏好若干有理分数的维度。这些分数对应均匀多胞体的结构 (如平面中的三角形与三维空间中的四面体) 。在对称条件下，优化过程会自动找到高对称度解。

几何变形:

若打破特征均匀性 (使某一特征更密集或更重要) ，多胞体会变形，有时平滑、有时突然跳变至新配置 (相变) 。例如正五边形随着稀疏性变化可逐渐拉伸，超过阈值后则可能坍缩成两个对跖对并忽略稀疏特征——这是在两个损失极小值间切换的离散跃迁。

多胞体 ↔ 低秩矩阵对应:

特征向量的排列 (\(W\) 的列) 直接决定 \(W^\top W\)。秩为 \(m\) 的半正定格拉姆矩阵等价于 \(\mathbb{R}^m\) 中的点配置 (旋转不变) 。因此，搜索 \(W^\top W\) 本质上相当于寻找单位球上的最优几何布局。

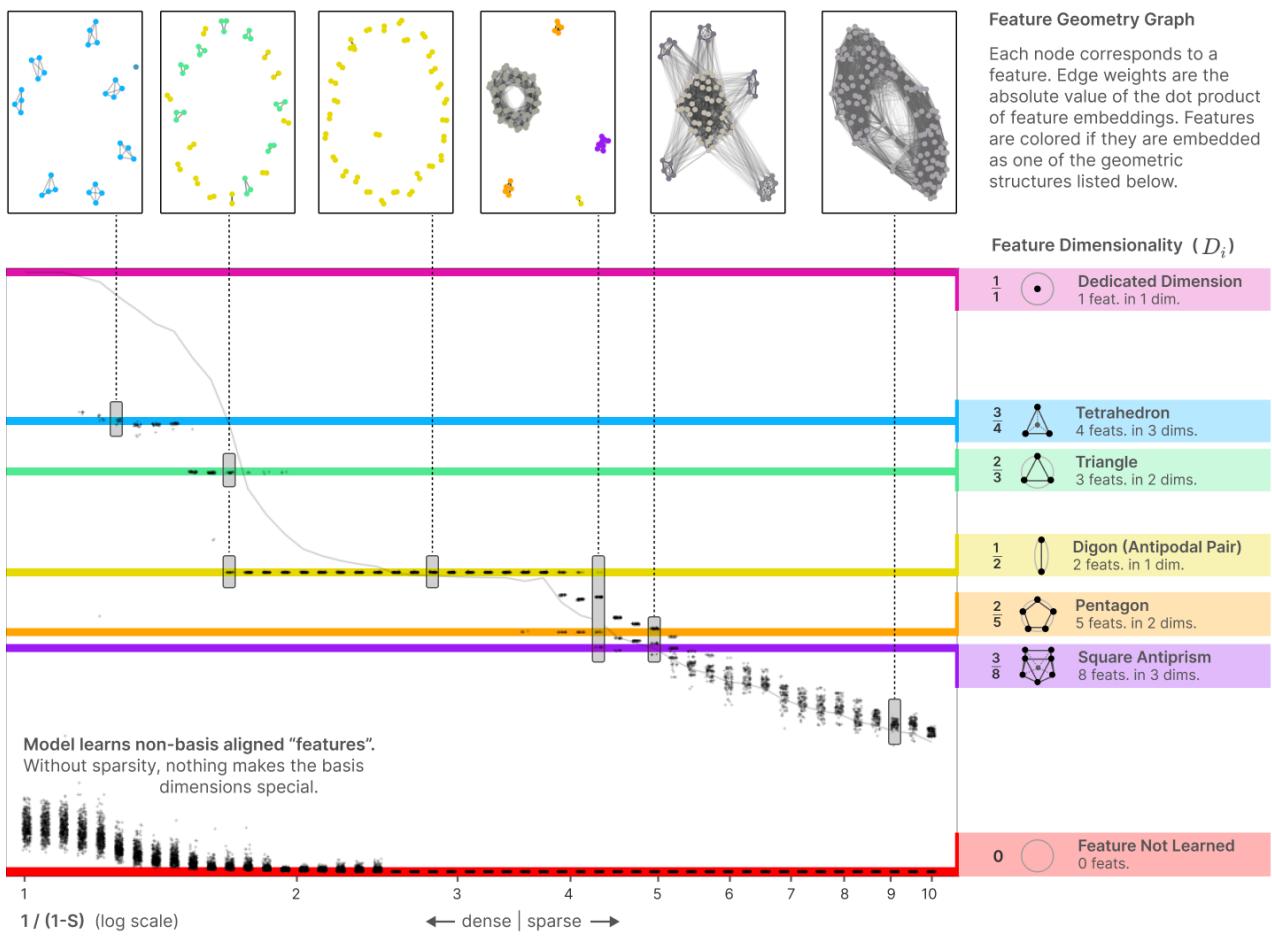
特征维度聚集在与多胞体对应的分数上；配置随稀疏度变化而变。

每个点代表特征维度 \(D_i\) 与稀疏度的关系。水平线对应特定几何构型 (二角形、三角形、四面体、五边形……) 。

这一几何视角优雅且出乎意料，表明叠加并非随机压缩，而是一种具高度结构与典范解的打包优化问题。

叠加状态下的计算

至此我们已见到网络可在叠加状态中存储和恢复特征。但它能否在叠加状态下计算？论文用一个精巧的玩具例验证: 逐元素计算 \(y = |x|\)。

为何选择绝对值?

绝对值的 ReLU 分解简洁且著名:

\[ |x| = \mathrm{ReLU}(x) + \mathrm{ReLU}(-x). \]

这一分解依赖 ReLU 非线性且每个输入仅需极少神经元。若模型能在特征叠加时计算绝对值，则证明叠加状态下的有效计算是可能的，并揭示自然的特权基 (隐藏层需使用 ReLU) 。

实验简述:

  • 输入 \(x\): 稀疏且允许取负 (非零项从 \([-1,1]\) 均匀采样) ；目标 \(y=|x|\)。
  • 模型: \(h = \mathrm{ReLU}(W_1 x)\)，\(y' = \mathrm{ReLU}(W_2 h + b)\)。其中 \(W_1\)、\(W_2\) 独立。
  • 测试: 改变 \(n, m\)、特征稀疏性与重要性，检查隐藏层权重与神经元含义。

实验结果:

  • 密集区: 模型学习出可解释电路——每个输入特征由两个神经元编码 (正侧与负侧) ，隐藏单元多为单语义。
  • 稀疏增大: 模型开始将多个“绝对值电路”打包于相同神经元中。神经元变得多语义但计算仍可靠。
  • 极稀疏区: 几乎所有神经元都高度多语义，但网络仍可同时近似计算多个特征的绝对值。

关键洞察:

  • 叠加中不仅能存储，也能计算。特征共享神经元的同时仍可路由和组合有效信号。
  • 特权基 (隐藏的 ReLU 神经元) 仍具意义: 特征更倾向对齐，但对齐度受稀疏性影响。

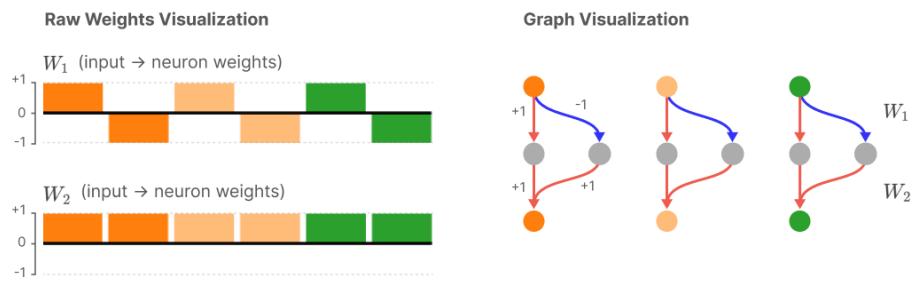
随着稀疏度增大，神经元由单语义转为多语义，计算仍保持正确。

每个面板展示不同稀疏度下的神经元堆叠。模型从单语义 (顶部) 过渡到多语义 (底部) ，依旧可准确计算绝对值。

机制模体: 带抑制的非对称叠加

一种常见模式是非对称叠加: 例如，一个神经元以不同幅度表示特征 \(a\)、\(b\) (如 \(W=[2,-1/2]\)) ，另一神经元用反向输出权重平衡优先级。为抵消代价高的正干扰，一个抑制神经元主动抑制多余激活，使正干扰转化为负干扰 (被 ReLU 忽略) 。此电路小而有效，确保在叠加状态下稳定计算。

与对抗性脆弱性的联系

叠加的重要、实证后果之一是: 干扰项 (即 \(W^\top W\) 中的小型非对角项) 天然为对抗扰动提供抓手。

  • 非叠加、正交情况 : 特征 \(i\) 的有效投影 \((W^\top W)_i \approx e_i\)，扰动其他方向不会显著改变它。
  • 叠加情况 : \((W^\top W)_i \approx e_i + \varepsilon\)，其中 \(\varepsilon\) 含多种微弱交叉项。攻击者可精心组合这些方向，虽范数小却能显著改变激活。

作者通过测量不同稀疏度下的对抗脆弱性 (最优 \(L_2\) 扰动下损失提升比例) 发现，其随叠加程度显著增长——特征越密集共享同维度，脆弱性越高，甚至可上升数倍。

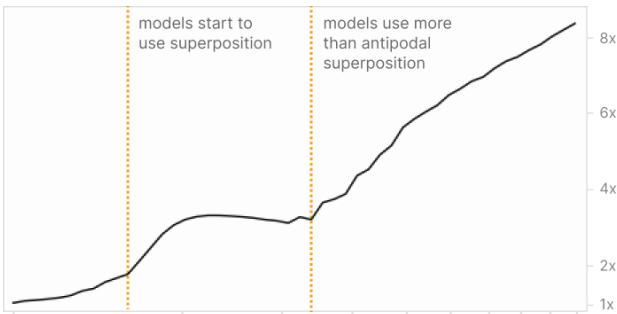
对抗脆弱性随每维度特征数/叠加程度上升而增强。

上图: 随稀疏度增长的对抗脆弱性。下图: 每维度特征数 (平均特征维度倒数) 。二者走势密切关联。

启示:

  • 叠加提供了对抗脆弱性发生的直观机制: 众多微耦合项聚合后可被利用。
  • 存在潜在权衡: 减少叠加可提升鲁棒性，但可能损失模型容量，除非改变架构或训练方式 (见下方策略) 。

对可解释性和安全性的影响

叠加现象是许多可解释性难题的核心:

  • 若特征与基方向对齐且单语义，特征枚举等于神经元枚举——易于机制性分析。
  • 若特征处于叠加状态，网络可能模拟指数级的有效特征，这些特征不再与单一神经元一一对应，枚举成为复杂稀疏编码问题。

作者提出，“解决叠加”指任何能枚举或展开模型特征的方法。若能解决，将恢复许多关键的可解释性能力:

  • 将整个分布的激活分解为纯特征；
  • 使网络回路分析更加可行；
  • 提供更可信的安全验证 (确保特定特征回路不存在) 。

但在大型模型中解决叠加极困难: 可能需巨量过完备稀疏分解或改动架构。论文给出了三种高层策略。

三种缓解或解决叠加的策略

  1. 避免叠加的模型
  • 方法: 强化 L1 激活稀疏性；采用架构提升每计算量的有效神经元数 (如 MoE) ；或训练正则化惩罚干扰。
  • 权衡: 除非架构提供额外容量，否则性能可能下降。叠加本身是固定神经元数下的一种容量压缩。
  1. 事后解码: 寻找过完备特征基
  • 将隐藏层激活视为压缩测量，利用稀疏编码/压缩感知恢复特征坐标。
  • 权衡: 大模型计算成本极高 (寻找数千倍过完备基) ，但模型结构与性能保持不变。
  1. 混合策略
  • 在训练中略作修改以减少叠加或提高后期解码性 (如几何偏置正则、检查点、定向稀疏化) 。
  • 权衡: 折中方案，潜在可行但需谨慎设计与验证。

乐观信号在于: 叠加似乎是一种相态——存在几乎无叠加的区域。这意味着可以通过特定训练或架构策略，以计算或工程代价将模型推过相变边界。

局限性与开放问题

这些玩具模型刻意简化，不意味着其中现象完全适用于大型网络。该工作旨在阐明合理机制并提出需实证验证的假设。论文与本文都留下了若干开放问题:

  • 真实模型中叠加程度几何？能否估计特征稀疏性与重要性分布？
  • 是否可设计可靠恢复真实网络层过完备特征基的实用算法？
  • 叠加如何随模型规模扩展？增大规模会减少还是加剧？
  • 哪类计算适合在叠加下高效实现？
  • 压缩感知理论是否能给出特定稀疏度与维度下可打包特征数的严格界限？
  • 训练方案 (对抗训练、替代非线性、MoE 稀疏结构) 能否有益地改变相变边界？

作者也提到若干独立实验复现、理论解 (如 \(n=2, m=1\) 的精确求解) 及后续研究，支持主效应的稳健性。

总结

《叠加的玩具模型》为理解多语义神经元提供全新视角: 它们未必是错误或训练噪声，而可能是以有限容量最佳表示稀疏特征的自然结果。主要见解:

  • 当特征稀疏且非线性可选择性过滤干扰时，叠加出现；
  • 特征进入叠加状态的过程尖锐且可从稀疏与重要性预测；
  • 叠加形成结构化几何 (多胞体) 而非随机噪声；
  • 网络可在叠加状态下稳健计算；
  • 叠加为对抗脆弱性提供合理机制。

对可解释性与安全性而言，叠加既是挑战也是方向。挑战在于它使神经元枚举复杂化；但方向在于，作为结构化相现象，存在原则方法可避免或解码它。

若你希望深入体验，原论文提供可运行的实验笔记本与代码。对可解释性研究者来说，问题已不在于叠加是否存在——它确实在合理的范畴内出现——而在于其在大规模模型中的重要程度，以及如何选择与之共存 (解码) 或规避 (减少叠加的架构) 。两条路径皆具科学意义与实践价值。

延伸阅读

  • 原始论文: Elhage 等，《Toy Models of Superposition》 (2022)
  • 相关主题: 压缩感知、解耦表示、对抗样本机制

致谢

本文是对 Elhage 等人论文的浓缩教学式解读，旨在阐明其主要思想、实验与启示。详细内容、证明、扩展结果和代码请参阅原论文及其补充笔记本。