想象一下教一个孩子认识猫。他们学得非常好。然后你教他们认识狗——突然之间，他们再也认不出猫了。这个令人困惑的场景正是人工智能每天所面临的现实。这被称为灾难性遗忘 : 当机器学习模型学习一个新任务时，它往往覆盖掉之前的知识，从而导致性能急剧下降。

这是持续学习 (又称终身学习) 的核心挑战: 我们如何构建一个智能系统，使其能够按顺序学习新技能, 而不忘记旧技能 ?多年来，研究人员提出了许多实用的方法来应对这一问题，一般可分为三大类:

  1. 基于记忆的方法: 保存旧任务的样本，并与新数据混合进行训练 (通常称为重放) 。
  2. 基于正则化的方法: 在目标函数中加入惩罚项，使参数与先前学习的任务保持一致。
  3. 基于扩展的方法: 通过扩大网络结构来容纳新知识。

尽管这些方法提升了持续学习的效果，但该领域一直缺乏一个统一理论。这些策略真的是根本不同的吗？还是它们其实是同一原理的不同实现？记忆重放 (rehearsal) 到底如何影响模型的泛化能力而非仅仅避免遗忘？

最近的一篇研究论文—— 《理想的持续学习者: 一个永不遗忘的智能体》 ——以一个大胆的目标来回答这些问题: 定义一个在数学意义上完美的学习者，它从设计上就不会遗忘。基于这一理论构造，作者揭示了持续学习、多任务学习、优化理论乃至经典控制系统之间的深层联系。

让我们一起深入探讨如何设计一个拥有完美记忆的理想学习者。

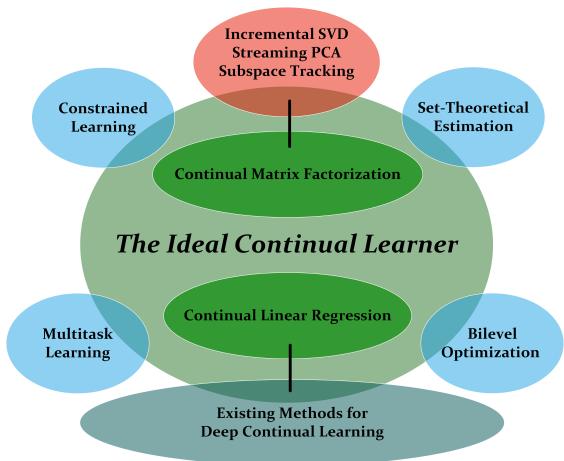
一张概念图，展示了理想的持续学习者如何连接多任务学习、双层优化和约束学习等多个领域。

图 1: 理想的持续学习者 (ICL) 是连接多任务学习、双层优化和约束学习等不同领域的枢纽。

永不遗忘的基本规则

在持续学习中，任务按序到达——\(t = 1, 2, \ldots, T\)。每个任务都有自己的数据集和目标函数 \(L_t(\boldsymbol{w})\)，其中 \( \boldsymbol{w} \) 表示模型的参数。任务 \(t\) 的所有全局最优解集合记为 \( \mathcal{G}_t \)。

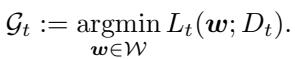
任务 t 的全局最优解集合。

最终目标是找到一个单一的 \( \boldsymbol{w} \)，使其在所有任务上都表现最优。为了实现这一点，论文提出了一个基础假设:

假设 1 (共享多任务模型) : 存在至少一个跨所有任务的共同全局最优解——数学表达为:

\[ \bigcap_{t=1}^{T} \mathcal{G}_t \neq \emptyset. \]

这个假设虽然强，但至关重要。如果所有解集的交集为空，那么遗忘将不可避免——没有模型能够同时满足所有任务。通过假设共享解存在，作者可以专注于如何高效地发现并保留它。

这一假设也绕过了一个关键的计算障碍: 确定全局最优解集的交集是否存在是一个 NP 难问题。共享多任务模型假设使理想持续学习者在理论上易于分析。

定义理想的持续学习者 (ICL)

在铺垫完成后，ICL 的定义既简单又深刻。它以递归方式运行: 从所有可能的模型空间开始 (\(\mathcal{K}_0 = \mathcal{W}\)) ，ICL 学习任务 1 并存储其全部最优解 (\(\mathcal{K}_1 = \mathcal{G}_1\)) 。当学习任务 2 时，它仅在此前的最优解集合中搜索；学习任务 3 时，则在所有历史解集的交集中搜索，以此类推。

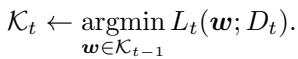
理想的持续学习者的递归定义。

形式上，

\[ \mathcal{K}_t = \operatorname*{argmin}_{\boldsymbol{w} \in \mathcal{K}_{t-1}} L_t(\boldsymbol{w}). \]

由此生成一个嵌套序列:

\[ \mathcal{W} = \mathcal{K}_0 \supseteq \mathcal{K}_1 \supseteq \mathcal{K}_2 \supseteq \cdots \supseteq \mathcal{K}_T. \]

可以将 \( \mathcal{K}_t \) 看作学习者的知识状态——一个不断精炼的表示，包含它迄今为止应用任务中的所有学习成果。就像人类专家将庞大的学习内容浓缩为核心公式一样，ICL 仅保留必要的信息，而不会遗忘已有知识。

“理想”一词说明它是一个理论模型。对于复杂神经网络而言，求全局最优解集合在计算上不可行，但将其视为理论构造，可以帮助研究者推导出对实际持续学习者应遵循的原则性洞察。

完美学习者的特性

ICL 具备两个关键特征，使其永不遗忘:

  1. 充分性——它不会遗忘。 在共享多任务假设下，ICL 在第 \(t\) 步的解集等于所有已学习任务解集的交集:

    \[ \mathcal{K}_t = \bigcap_{i=1}^t \mathcal{G}_i. \]

    每一个属于 \( \mathcal{K}_t \) 的点都对所有之前的任务保持最优，保证零遗忘。

  2. 最小性——它只存储必要的信息。 学习者必须保留完整的解空间信息。如果只保存子集或部分表示，则未来兼容解可能丢失。保留完整解集 (或等效信息，如梯度方程) 是避免遗忘的最小条件。

因此，ICL 不仅最优，而且具有信息论上的高效性: 存储更少会导致遗忘，存储更多则没有意义。

统一全局: 各领域中的 ICL

ICL 的魅力在于它的多面性。论文证明，这一递归定义可以优雅地映射到机器学习中的多个熟悉框架。

ICL 作为双层优化器

在每一步中，ICL 都解决一个受到前序任务约束的上层优化问题——这就是一种双层优化形式。

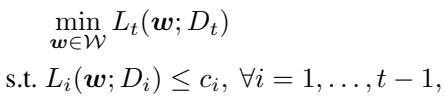
ICL 被表述为一个约束优化问题，其中前序任务的损失不能超过它们的最小值。

每一步优化为:

\[ \min_{\boldsymbol{w}} L_t(\boldsymbol{w}) \quad \text{s.t.} \ L_i(\boldsymbol{w}) \le c_i, \ \forall i < t, \]

其中 \( c_i \) 为任务 \(i\) 的最小损失。

对于凸优化问题，这些约束等价于要求所有先前任务的梯度为零，从而确保学习者不会“反向遗忘”。

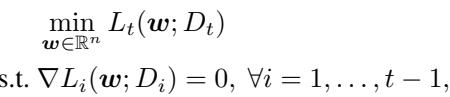
对于凸问题，ICL 的约束等同于强制所有先前任务的梯度为零。

保存梯度或最小损失值即可提供足够的信息来防止遗忘。

ICL 作为多任务学习者

更有趣的联系在于 ICL 与多任务学习的等价性，在多任务学习中，所有任务通过联合损失同时训练:

\[ \sum_{i=1}^{t} \alpha_i L_i(\boldsymbol{w}), \]

其中权重 \(\alpha_i\) 为正。

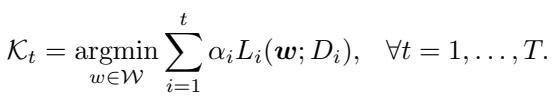
ICL 找到的解集与多任务学习得到的解集相同。

当共享解存在时，序列化的 ICL 过程与多任务学习得到的最优解集相同。

这解决了长期以来的争论: 在正确的假设下，持续学习与多任务学习是等效的。顺序学习并不是妥协，它可以同样强大。

ICL 的实践: 两个关键示例

论文通过两个典型示例将理论与实践相结合，直接对应深度持续学习的实际情况。

示例 1: 持续线性回归

每个任务旨在拟合线性模型，最小化 \(L_t(\boldsymbol{w}) = \|X_t \boldsymbol{w} - y_t\|_2^2\)。其解集 \(\mathcal{G}_t\) 形成一个仿射子空间。

传统方法在这些子空间之间交替投影 (图 2a) ，虽然简单但容易遗忘。 ICL 则求解第一个任务，存储其完整解子空间，并约束后续优化与其保持兼容 (图 2b) 。

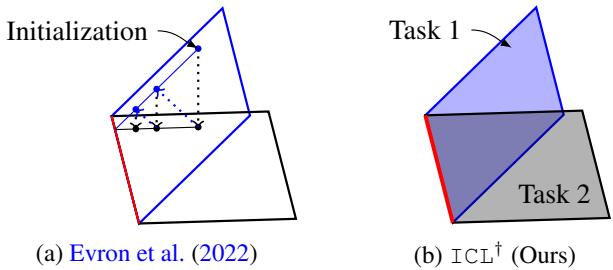
比较交替投影方法 (a) 与 ICL 方法 (b) 在两项线性回归任务中的表现。ICL 直接找到了解空间的交集。

图 2: 与交替投影方法不同，ICL 将新的优化严格限制在已知解空间的交集内。

具体而言，ICL 存储一个特定解 \( \hat{\boldsymbol{w}}_{t-1} \) 和一组标准正交基 \( \boldsymbol{K}_{t-1} \)，该基张成先前数据矩阵的共享零空间。任何有效解均可写为 \( \boldsymbol{w} = \hat{\boldsymbol{w}}_{t-1} + \boldsymbol{K}_{t-1} \boldsymbol{a} \)，从而将每个新任务转化为系数 \( \boldsymbol{a} \) 的较小优化问题。

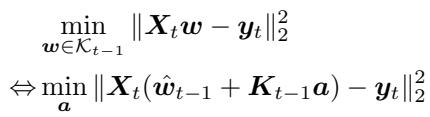
持续线性回归的 ICL 优化，转化为在更小系数向量 ‘a’ 上的搜索。

将搜索空间缩减到新系数，使得存储更紧凑、更新更高效。

这一机制与正交梯度下降 (OGD) ——一种流行的深度学习方法——高度相似。论文指出，OGD 实质上是在 ICL 目标上执行梯度下降，把这一实用算法与理论基础精确联系起来。

示例 2: 持续矩阵分解

另一个示例涉及矩阵分解 \( Y_t \approx UC \)，类似于主成分分析 (PCA) 。 每个任务提供一个新的数据子空间 \(S_t\)。

ICL 旨在找到捕捉所有已学子空间和的标准正交基:

\[ \sum_{i=1}^t S_i. \]

当新任务到来时:

  1. 将数据 \(Y_t\) 投影到旧子空间的正交补，以发现新信息；
  2. 通过 SVD 计算新空间的标准正交基；
  3. 通过连接该更新来扩展整体基。

这种扩展式理解为为什么更宽的神经网络遗忘更少提供了合理的解释——每增加一列都表示获取新的独立知识。相比固定宽度网络，ICL 给出了明确的数学依据来指导网络的扩展时机与方式。

从完美优化器到真实学习者

ICL 不仅是一个优化理论，也延伸到了统计学习理论领域，其中数据源自分布。它区分基于训练样本的经验解集与基于真实分布的理想解集。

在标准的 Lipschitz 连续性和有界假设下，作者推导出泛化界，用以衡量 ICL 相对于理想学习者的期望近似度。

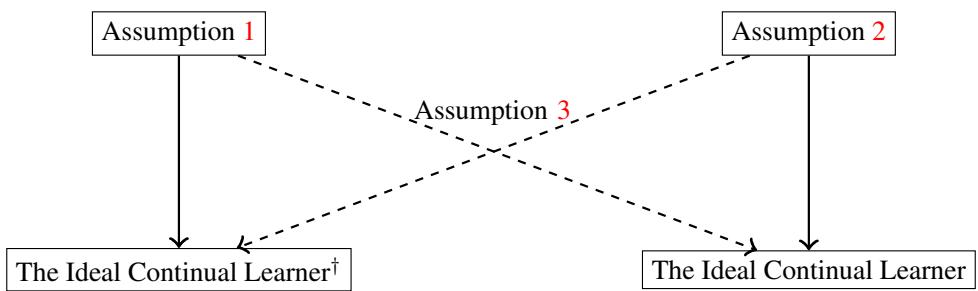
展示不同假设与 ICL 表现之间关系的示意图。实线箭头表示具备保证的性能，虚线箭头表示近似的性能。

图 3: 经验学习者与真实学习者之间的理论联系。虚线箭头表示在标准泛化假设下的近似保证。

两个主要结果如下:

  1. 定理 1: 当假设 1 成立时，ICL 的经验版本 (\( \text{ICL}^\dagger \)) 对所有真实任务都是近似最优的。
  2. 定理 2: 松弛版 ICL 允许在早期任务中出现微小偏差，仍保持近似最优，保证了实际可行性。

重放的理论基础

在持续学习中, 重放 (rehearsal) ——即重播已存样本——是否真的有益泛化，长期存在争论。ICL 对此给出了严格的数学界限。

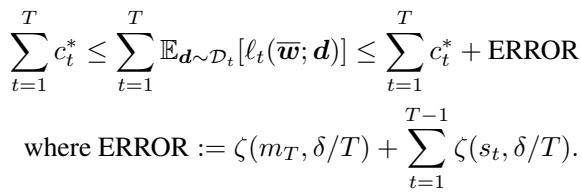
重放的泛化界说明总误差由多个误差项之和界定。

当为重放存储更多样本时，泛化误差会显著减小。

形式上，总泛化误差与每个先前任务保留的样本数量 \(s_t\) 成正比递减:

\[ \text{ERROR} = \zeta(m_T, \delta/T) + \sum_{t=1}^{T-1} \zeta(s_t, \delta/T), \]

其中 \(\zeta(\cdot)\) 表示统计不确定性。存储样本越多 → 误差越小。

值得注意的是，该界限只依赖于保留的样本数量，而非具体选择的样本。这与实证结果一致: 随机抽样往往与复杂的样本选择策略同效。换言之，当样本满足独立同分布 (i.i.d.) 时, 数量胜于技巧 。

结论: 条条大路通 ICL

理想的持续学习者为终身学习提供了统一的理论基础。其核心洞察包括:

  • 共同原理: 基于记忆、正则化和扩展的方法都是 ICL 的实用近似形态。
  • 深层联系: ICL 框架贯通了持续学习、多任务学习、双层优化、约束学习以及控制理论。
  • 量化理解: 它提出了首个重放泛化界，并阐明了为何扩展网络容量能有效防止遗忘。

尽管 ICL 在精确形式上无法直接实现，但其理论蓝图为未来算法指明了方向，帮助我们模仿一个永不遗忘的学习者。持续学习不再是一场与遗忘的永恒斗争，而是一段不断逼近这一理想——一个拥有完美记忆与无限适应力的智能体——的旅程。