引言

在现代机器学习的世界里，我们已经超越了仅仅预测“平均值”的时代。无论是个性化医疗、计算广告还是公共政策，最有价值的洞察往往隐藏在异质性 (heterogeneity) 之中——即理解某种效应如何在不同的人群亚组中变化。

例如，一种新药对整个人群的平均疗效可能平平，但对某个特定的基因亚组可能具有挽救生命的作用，而对另一个亚组则可能有害。简单的回归模型通常会忽略这些细微差别。

为了解决这个问题，研究人员转向了广义随机森林 (Generalized Random Forests, GRF) 。 这个由 Athey 等人推广的框架是估计异质性处理效应和变系数的黄金标准。它采用了强大的随机森林算法来局部求解统计估计方程。

然而，GRF 存在一个瓶颈。标准算法依赖于基于梯度的分裂准则 (gradient-based splitting criterion) , 这需要在树生成的每一步都对矩阵 (雅可比矩阵) 进行求逆。在高维设置下，或者当特征高度相关时，这个过程会变得计算昂贵且数值不稳定。

在这篇文章中，我们将探讨 Fleischer、Stephens 和 Yang 提出的一种新方法: 不动点树 (Fixed-Point Trees, FPT) 。 这种方法用不动点近似代替了昂贵的梯度步骤。结果如何？一种比原始方法快得多、更稳定且同样准确的方法诞生了——它为更大、更复杂的数据集开启了可扩展的因果推断大门。

背景: 广义随机森林

要理解不动点树的创新之处，我们首先需要了解广义随机森林 (GRF) 试图实现什么。

标准随机森林旨在最小化预测误差 (如回归中的均方误差) 。GRF 则更有野心。它们旨在估计一个感兴趣的参数 \(\theta^*(x)\)，该参数被定义为一个局部估计方程的解:

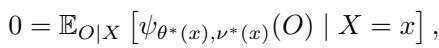
定义目标参数的估计方程。

在这里，\(\psi\) 是一个“得分函数 (score function) ”。例如，在分位数回归中，\(\psi\) 是一个检验函数；在工具变量中，它涉及协方差矩。目标是找到一个 \(\theta\)，使得在给定特征 \(X\) 的条件下，期望得分为零。

GRF 分两个阶段工作:

  1. 第一阶段 (树的训练) : 算法构建一个森林，将数据划分成观测值相似的“叶子”。
  2. 第二阶段 (估计) : 对于一个新的测试点 \(x\)，森林根据训练样本 \(i\) 落入与 \(x\) 相同叶子的频率来计算权重 \(\alpha_i(x)\)。

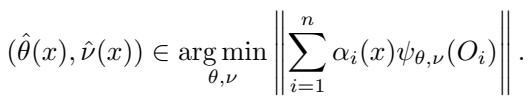
最终预测的加权估计方程。

最终的估计值通过求解如上所示的加权方程得到。GRF 的魔力在于第一阶段 : 当目标 \(\theta\) 无法直接观测 (如处理效应) 时，我们如何构建一棵树来将“相似”的数据点分组？

瓶颈: 基于梯度的分裂

任何决策树的核心都是分裂规则 (splitting rule) 。 树观察父节点 \(P\)，并试图将其分裂为两个子节点 \(C_1\) 和 \(C_2\)，以最大化两个子节点参数之间的差异 (异质性) 。

理想情况下，我们会基于子节点中真实的参数值来最大化一个准则 \(\Delta(C_1, C_2)\):

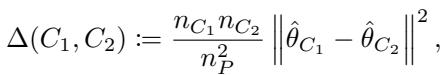
基于真实参数的理想分裂准则。

由于我们无法预先知道真实的参数 \(\hat{\theta}_{C_1}\) 和 \(\hat{\theta}_{C_2}\) (对每个可能的分裂都计算它们太慢了) ，标准 GRF 使用基于梯度的近似 (Gradient-Based Approximation) 。 它通过从父节点的参数 \(\hat{\theta}_P\) 出发采取单个牛顿-拉夫逊 (Newton-Raphson) 步来近似子节点中的参数。

这种近似导致了“Grad”估计量:

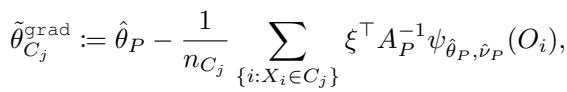
基于梯度的近似公式。

梯度的问题

仔细观察上面的方程。项 \(A_P^{-1}\) 代表雅可比矩阵的逆 。 雅可比矩阵 \(A_P\) 衡量了得分函数的曲率:

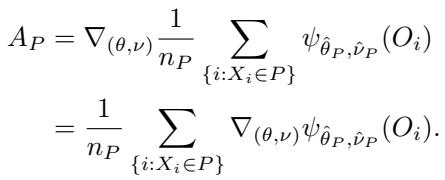
雅可比矩阵 A_P 的定义。

依赖 \(A_P^{-1}\) 引入了两个主要问题:

  1. 计算成本: 矩阵求逆的时间复杂度是 \(O(K^3)\)，其中 \(K\) 是参数 \(\theta\) 的维度。如果你正在估计一个包含许多参数的复杂模型，这一步会变得极其缓慢。
  2. 不稳定性: 如果你的特征高度相关 (多重共线性) ，矩阵 \(A_P\) 会变得“病态” (近奇异) 。对其求逆会导致巨大的数值爆炸，导致分裂准则表现异常。

作者在图 1 中展示了这种不稳定性。下图显示了当回归变量高度相关时会发生什么。“grad”方法 (橙色) 产生高方差的分裂，波动剧烈。而提出的“FPT”方法 (蓝色) 则保持完美稳定。

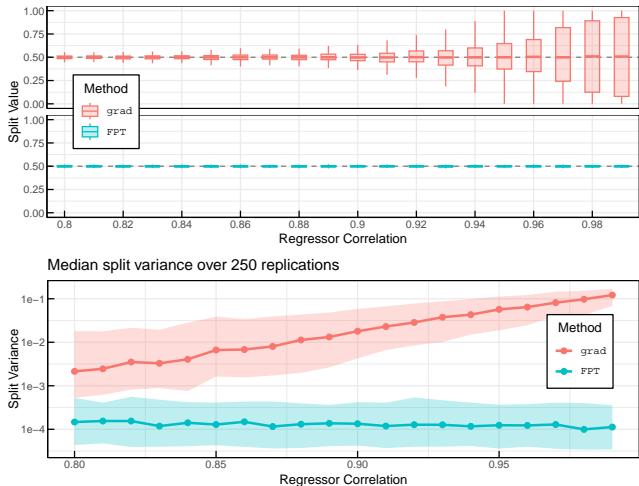
箱线图: 回归变量相关性下的分裂值。图 1: 分裂值 (上) 和分裂方差 (下) ，带有第 10 和第 90 百分位带，跨越 W_i,1 和 W_i,2 的相关性。

解决方案: 不动点树

研究人员提出了一种完全消除雅可比矩阵求逆需求的方法。他们称之为不动点树 (Fixed-Point Tree, FPT) 算法。

直觉

他们没有将参数估计视为需要牛顿步 (需要导数/雅可比矩阵) 的求根问题，而是将其重新构建为一个不动点迭代 。

标准不动点理论表明，在一定条件下，我们可以通过迭代应用一个函数来近似解。作者建议通过从父参数 \(\theta_P\) 向负得分方向迈出一“步”来近似子参数 \(\theta_{C_j}\)，步长由常数 \(\eta\) 缩放，且无需通过逆雅可比矩阵进行旋转。

FPT 近似看起来像这样:

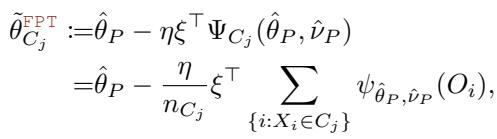
不动点树近似公式。

将其与上一节中的梯度公式进行比较。昂贵的矩阵 \(A_P^{-1}\) 不见了，取而代之的是标量 \(\eta\) 和选择矩阵 \(\xi\)。这一看似简单的改变将计算复杂度从 \(O(K^3)\) 实质上降低到了 \(O(K)\)。

它能找到相同的分裂吗？

你可能会担心移除雅可比矩阵会改变梯度的“方向”，导致次优的分裂。然而，对于决策树而言，我们只关心分裂的排名 。 我们需要知道哪个分裂更好，而不是改进的确切幅度。

作者证明了 FPT 准则在渐近上等同于由雅可比矩阵加权的“预言机”准则。更直观地说, 图 2 展示了不同分裂阈值下的分裂准则值。

图 2: 跨越候选分裂 (C_1(t), C_2(t)) 的准则值，阈值 t 在 [0, 1] 范围内。每个准则下的最优分裂位置由相应的垂直线给出。

请注意，虽然曲线具有不同的高度 (尺度) ，但它们的峰值——最优分裂点——几乎完美对齐。这意味着 FPT 找到了与计算昂贵的梯度方法实际上相同的结构。

实现: 伪结果技巧

为了高效地实现这一点，GRF 使用了“伪结果 (pseudo-outcomes) ”。其核心思想是将复杂的参数估计问题转化为标准的回归问题。我们为每个数据点计算一个“假标签” (伪结果) ，然后对这些标签运行标准的 CART (分类与回归树) 算法。

对于标准梯度方法，伪结果 \(\rho_i^{\text{grad}}\) 涉及逆雅可比矩阵:

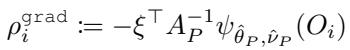
基于梯度的伪结果定义。

对于不动点方法 , 伪结果 \(\rho_i^{\text{FPT}}\) 简化为负得分函数:

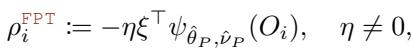
不动点伪结果定义。

算法只需在父节点计算这些残差，并将它们输入到标准的回归树分裂器中。这使得利用高度优化的建树库成为可能。

应用: 异质性处理效应

GRF 最流行的用途之一是估计异质性处理效应 (Heterogeneous Treatment Effects, HTE) 。在这种设置下，我们有结果 \(Y\)，处理 \(W\) 和协变量 \(X\)。我们想知道 \(W\) 对 \(Y\) 的影响如何随 \(X\) 变化。

模型通常构建为:

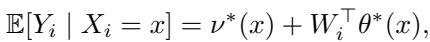
变系数的条件期望模型。

这里，\(\theta^*(x)\) 代表处理效应。

使用 FPT 方法，我们可以为该模型定义特定的伪结果，其计算速度极快。作者为这些线性模型引入了一种特定的加速方法，即对父参数也使用“一步”近似，进一步减少了开销。

这种设置下的 FPT 伪结果本质上变成了回归变量与残差之间的交互项:

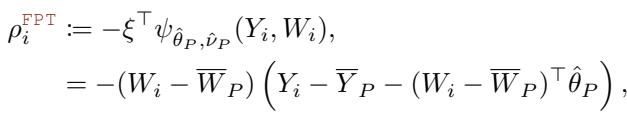
VCM/HTE 模型中的 FPT 伪结果方程。

这完全避免了 \(O(K^3)\) 的成本，当测试多个并发处理 (例如，具有许多分支的 A/B/n 测试) 时，这是一个改变游戏规则的优势。

实验结果

理论上的好处是显而易见的，但 FPT 在实践中表现如何？作者在变系数模型 (VCM) 和异质性处理效应 (HTE) 上进行了广泛的模拟。

1. 计算速度

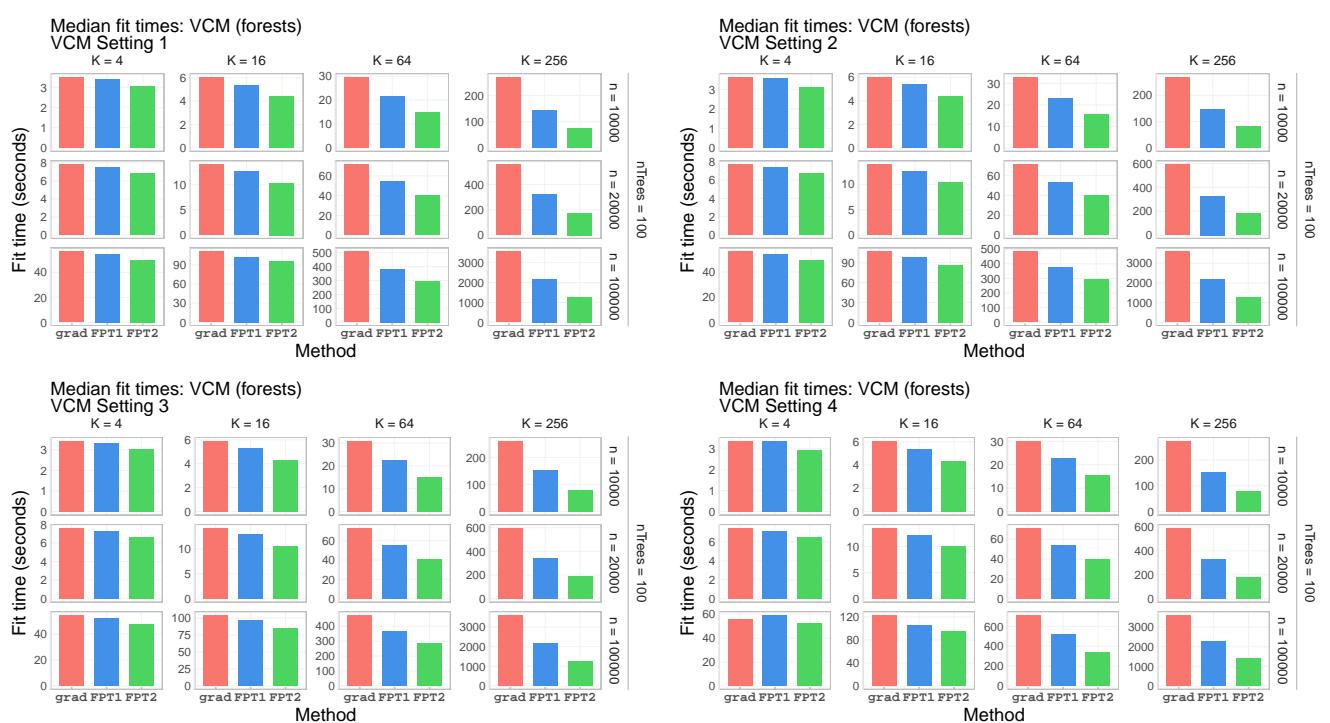
论文的主要主张是速度。 图 3 显示了随着目标参数维度 (\(K\)) 的增加，FPT 相对于标准梯度方法的加速比。

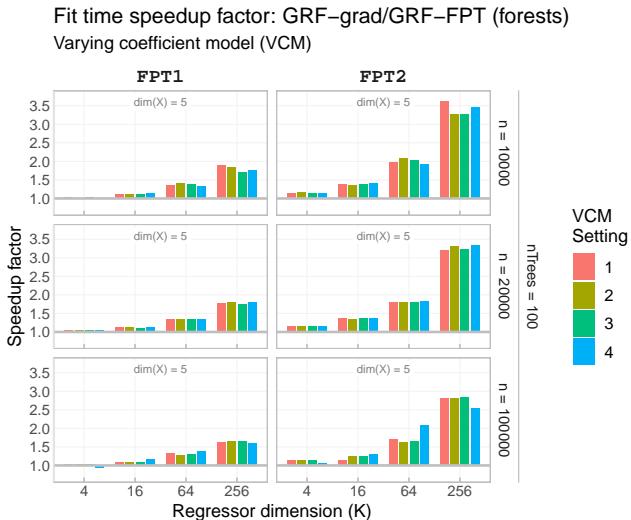
图 3: VCM 计时实验中 GRF-FPT 相比 GRF-grad 的加速比。

随着维度 \(K\) 的增长 (从 4 到 256) ，加速变得巨大——在高维设置下，FPT 的速度是原来的 3.5 倍以上 。 即使在低维度下，也存在持续的性能提升。

观察图 5 中的绝对拟合时间，我们可以看到，虽然梯度方法 (红色) 的时间随着 \(K\) 的增加而爆炸式增长，但 FPT 方法 (绿色和蓝色) 仍然保持高效。

图 5: 表 2 设置和大样本 n 设置 (表 1) 下的 VCM 计时实验的绝对拟合时间。

2. 统计准确性

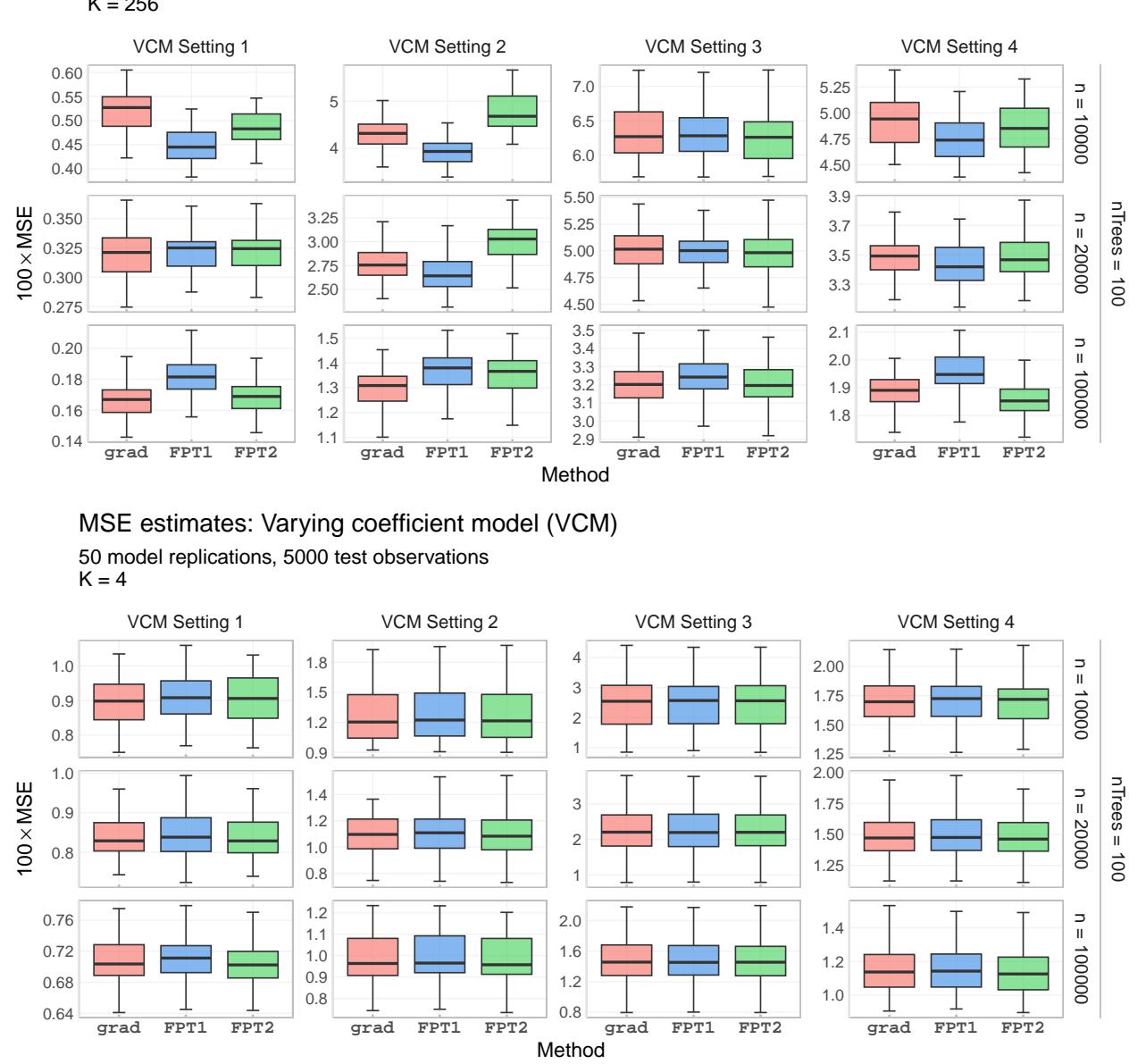
如果估计结果是错误的，速度再快也没用。作者测量了参数估计的均方误差 (MSE) 。

图 6 将梯度方法的 MSE 与 FPT 进行了比较。曲线在很大程度上是重叠的，这表明 FPT 为了获得速度提升几乎没有牺牲统计准确性 。 在某些高维情况下 (顶行) ，FPT 的表现实际上略好一些，这可能归因于前面讨论的梯度方法的数值稳定性问题。

图 6: 大样本 n 设置下 VCM 的 MSE 估计。

3. 真实世界数据: 加州房价

为了在真实数据上说明该方法，作者将 FPT 应用于著名的加州房价数据集。他们将房价建模为各种特征 (收入、卧室数、人口) 的函数，并允许这些特征的系数在地理上 (按经纬度) 变化。

这是一个经典的“变系数模型”。结果地图( 图 4 )显示了明显的地理模式。

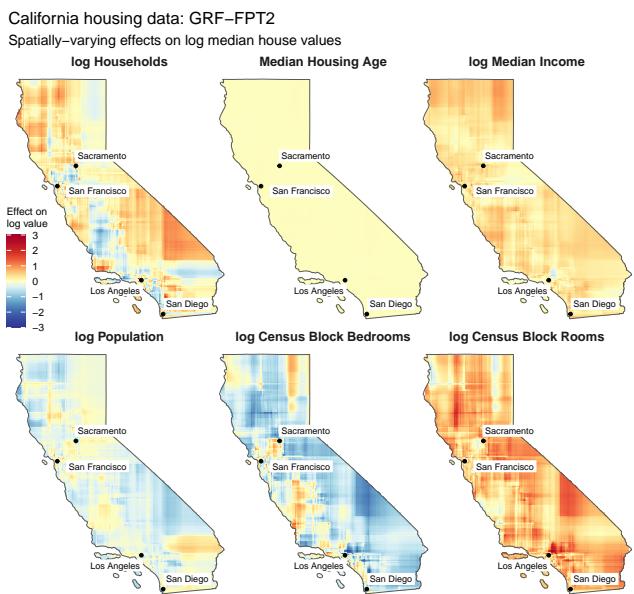
图 4: 地理上变化的 GRF-FPT2 估计值。

例如，看看“对数家庭数 (log Households) ”的影响 (左上角) 。在人口密集的城市中心 (洛杉矶，旧金山) ，这种影响是负面的 (红色/橙色) ——更拥挤可能降低价值。在农村地区 (蓝色) ，这种影响是正面的——更多的邻居可能标志着一个理想的社区。FPT 算法高效地捕捉到了这些复杂的空间异质性。

结论

广义随机森林改变了我们分析异质性效应的方式，但其对雅可比矩阵求逆的依赖一直是性能和稳定性的长期拖累。

不动点树 (Fixed-Point Tree, FPT) 算法消除了这一障碍。通过将基于梯度的分裂准则替换为不动点近似，FPT 提供了:

  1. 速度: 消除了 \(O(K^3)\) 的矩阵求逆，实现了倍数级的加速。
  2. 稳定性: 消除了对多重共线性和病态矩阵的敏感性。
  3. 准确性: 保持了原始 GRF 严格的一致性和渐近正态性保证。

对于处理高维数据或复杂因果模型的从业者和研究人员来说，FPT 将繁重的计算任务转化为可扩展的工作流。它使我们能够提出更复杂的问题——估计跨越多种处理或特征的效应——而无需为答案等待数天。