引言

在人工智能的世界里，知识图谱 (Knowledge Graphs, KGs) 是幕后的无名英雄。它们为你谷歌搜索的侧边栏提供支持，驱动亚马逊的产品推荐，并帮助复杂系统理解“巴黎”是“法国”的首都。为了让机器学习利用这些图谱，我们使用知识图谱嵌入 (Knowledge Graph Embedding, KGE) 模型。这些模型将实体 (如“巴黎”) 和关系 (如“是…的首都”) 转化为数学向量和矩阵。

多年来，像 TransE 和 RotatE 这样的模型一直是黄金标准。它们高效且通常有效。然而，最近的一篇研究论文揭示了一个深埋在这些流行模型数学原理中的基本逻辑缺陷。研究人员将其称为 “Z-悖论” (Z-paradox) 。

想象这样一个场景: 你出演了一部电影。你的朋友也出演了同一部电影。你的朋友还出演了 另一部 不同的电影。这是否自动意味着 你 也出演了那第二部电影？显然不是。但令人惊讶的是，许多最先进的 AI 模型在数学上强制这种联系成立。它们仅仅因为数据的结构看起来像字母“Z”，就“产生幻觉”认为存在这种关系。

在这篇文章中，我们将深入探讨论文 “MQuinE: a cure for Z-paradox in knowledge graph embedding models” 。 我们将探索什么是 Z-悖论，证明现有模型为何会失败，并研究解决方案: 一种名为 MQuinE (Matrix Quintuple Embedding，矩阵五元组嵌入) 的新模型，它使用一种巧妙的矩阵架构来修复这一缺陷，同时不损失表达能力。

背景: 知识图谱嵌入的现状

在解决这个悖论之前，我们需要理解机器是如何“阅读”知识图谱的。知识图谱是事实的集合，表示为三元组: (头实体, 关系, 尾实体) , 即 \((h, r, t)\)。例如: (莱昂纳多·迪卡普里奥, 出演了, 盗梦空间)。

KGE 模型的目标是学习一个打分函数 \(s(h, r, t)\)。如果三元组是真实事实，分数应该很低 (或很高，取决于惯例；在本文中，越低越好，接近 0) 。如果事实是假的，分数应该很高。

在过去的十年中，研究人员开发了各种“几何”方法来表示这些关系。

  1. 基于平移的模型 (例如 TransE) : 将关系视为向量平移。如果你取“国王”的向量加上“女人”的向量，你应该得到接近“女王”的向量。数学上表示为: \(\mathbf{h} + \mathbf{r} \approx \mathbf{t}\)。
  2. 基于旋转的模型 (例如 RotatE) : 将关系视为复数向量空间中的旋转。
  3. 双线性模型: 使用矩阵乘法来捕捉交互。

Table B.2: The score functions of different KGE models.

如上表所示，该领域已经从简单的距离函数演变为复杂的张量分解。然而，表达能力——即模拟不同逻辑模式 (如对称性或层级结构) 的能力——是主要的争夺点。MQuinE 的作者认为，尽管取得了这些进展，一个特定的逻辑陷阱仍被忽视了。

问题所在: Z-悖论

这篇论文的核心贡献是发现了 Z-悖论 。 这是一种模型缺乏“表达能力”来区分两种不同逻辑可能性的情况。

可视化悖论

让我们看看导致这个问题的结构。我们要有四个实体 (\(e_1, e_2, e_3, e_4\)) 和一个关系 \(r\)。

  1. \(e_1\) 与 \(e_2\) 有关系。
  2. \(e_3\) 也与 \(e_2\) 有关系。
  3. \(e_3\) 与 \(e_4\) 有关系。

问题是: \(e_1\) 与 \(e_4\) 有关系吗?

在现实世界中，答案是“可能”或“不一定”。然而，作者发现对于基于平移的模型，答案在数学上被迫为“是”。

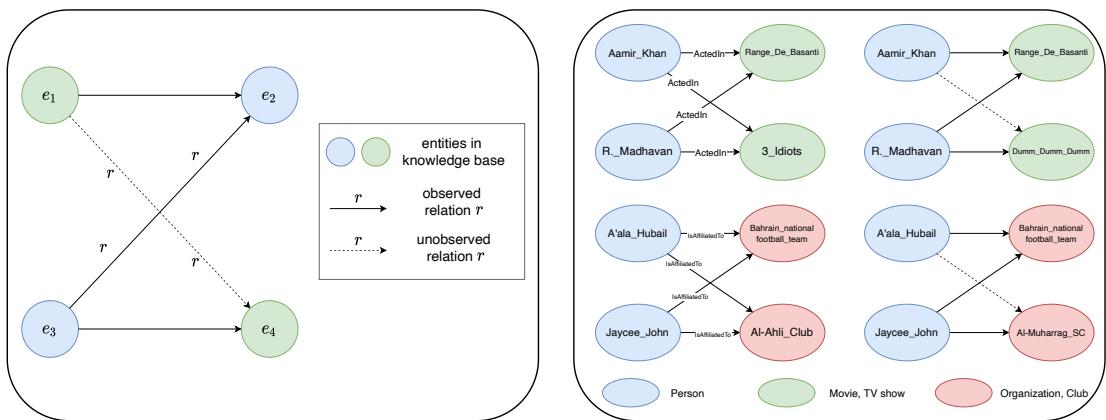
Figure 1.1: Left panel: an illustration of Z-paradox. Right panel: an illustration of Z-paradox in the YAGO3-10 dataset.

上图完美地展示了这一点。

  • 左图: 显示了 Z 形结构。实线箭头是已知事实。虚线箭头 (\(e_3 \to e_4\)) 也是已知的。Z-悖论在于，即使 \(e_1\) 和 \(e_4\) 之间不存在关系，模型也会推断出这种连接 (底部虚线) 。
  • 右图: 来自 YAGO3 数据集的真实案例。
  • *左上: * 阿米尔·汗出演了《芭萨提的颜色》。马德哈万出演了《芭萨提的颜色》和《三傻大闹宝莱坞》。模型推断阿米尔·汗出演了《三傻大闹宝莱坞》。在这个特定案例中，这恰好是真的。
  • *右上: * 阿米尔·汗出演了《芭萨提的颜色》。马德哈万出演了《芭萨提的颜色》和《Dumm Dumm》。模型推断阿米尔·汗出演了《Dumm Dumm》。 这是假的。 但模型无法控制自己；数学强制了这种连接。

失败的数学证明

为什么会发生这种情况？这归结为 TransE 和 RotatE 等模型使用的打分函数。这些模型依赖于测量变换后的嵌入之间的距离。

作者正式定义该悖论如下:

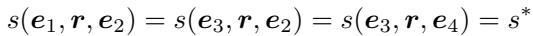
Equation defining the Z-paradox condition

如果 Z 形结构的三个“边”的分数都等于最优分数 \(s^*\) (通常为 0) ，且这意味着第四条边 (\(e_1 \to e_4\)) 的分数 必须 也是 \(s^*\)，那么该模型就患有 Z-悖论。

让我们证明为什么基于平移的模型会失败。大多数平移模型定义了一个打分函数 \(s(h,r,t)\)，它可以分离为头实体的函数和尾实体的函数: \(\|f(h,r) - g(t,r)\|\)。理想情况下，对于一个真实事实，这个距离为 0，意味着 \(f(h,r) = g(t,r)\)。

如果我们拥有 Z 结构的这三个事实，我们就有以下等式:

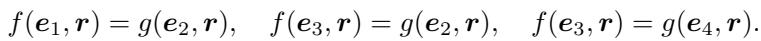
Equations showing the transitive property causing the failure

现在，看看当我们试图计算未观察到的三元组 \((e_1, r, e_4)\) 的分数时会发生什么:

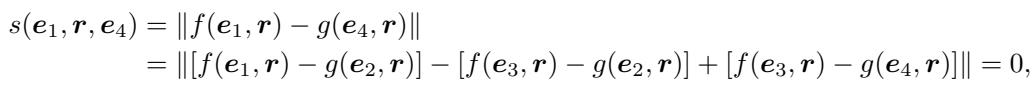
Derivation showing the score must be zero

由于距离函数的线性性质，各项完美抵消。分数变成了 0。模型 在数学上无法 预测这种关系为“真”以外的任何结果。无论你用多少数据进行训练都无济于事；架构本身就是局限。

这不仅仅是简单模型的问题。作者指出，即使是复杂的双线性模型 (如 DisMult 或 ComplEx) ，如果以特定方式设置 (例如使用正交矩阵) ，也会遭遇此问题。

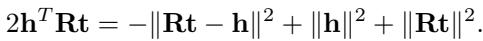
Equation showing bilinear models conversion to distance-based forms

解决方案: MQuinE

为了解决这个问题，研究人员提出了 MQuinE (Matrix Quintuple Embedding，矩阵五元组嵌入) 。这个名字来源于它使用 五个 矩阵来表示三元组中涉及的实体和关系。

目标是设计一个打分函数，能够:

  1. 打破导致 Z-悖论的线性依赖。
  2. 保留模拟复杂模式 (对称性、逆向性、层级结构) 的能力。

架构

在 MQuinE 中:

  • 实体 (\(h, t\)) : 由 对称矩阵 \(\mathbf{H}\) 和 \(\mathbf{T}\) 表示。
  • 关系 (\(r\)) : 由 三个矩阵 的元组表示: \(\langle \mathbf{R}^h, \mathbf{R}^t, \mathbf{R}^c \rangle\)。

打分函数定义为:

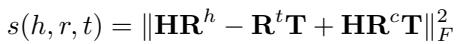
The MQuinE Score Function

让我们拆解这个方程: \(s(h,r,t) = \|\mathbf{HR}^{h} - \mathbf{R}^{t}\mathbf{T} + \mathbf{HR}^{c}\mathbf{T}\|_{F}^{2}\)。

  • \(\mathbf{HR}^h - \mathbf{R}^t\mathbf{T}\) : 这部分看起来类似于标准嵌入 (如 MQuadE) 。它处理头尾之间的基本变换。
  • \(+\mathbf{HR}^c\mathbf{T}\) : 这是 交叉项 。 这正是创新所在。通过引入一个将头实体、关系 (交叉) 和尾实体相乘的项，研究人员引入了一种非线性交互，破坏了我们在悖论证明中看到的“抵消”效应。

治愈的证明

这真的修复了 Z-悖论吗？作者通过证明来展示这一点: 使用 MQuinE，你可以拥有一组矩阵，使得 Z 模式的事实为真 (分数 = 0) ，但虚构的事实 \((e_1, r, e_4)\) 可以是真的也可以是假的 (分数 = 0 或 分数 > 0) 。模型拥有了 选择权。

他们提供了一个具体的矩阵构造:

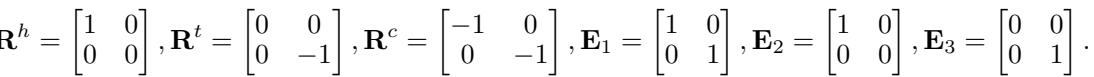
Matrix definitions for the proof

利用这些矩阵，他们展示了两种情况。 情况 1: 他们设置 \(E_4\)，使得模型预测第四条链接为 假 (分数 = 1) ，即使 Z 模式存在。

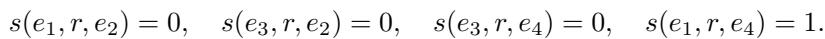
Result showing score is 1 (False)

情况 2: 他们设置不同的 \(E_4\)，使得模型预测第四条链接为 真 (分数 = 0) 。

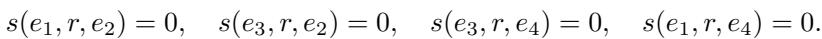
Result showing score is 0 (True)

因为 MQuinE 可以表示这两种情况，所以它从悖论中解放了出来。它不再受制于字母 Z 的几何结构。

保持表达能力

如果“修复”破坏了其他能力，那就是无用的。一个优秀的 KGE 模型必须处理各种关系类型:

  • 对称性: MarriedTo (如果 A 和 B 结婚，B 也和 A 结婚) 。
  • 逆向性: ParentOf 与 ChildOf。
  • 复合性: 父亲 的 父亲 是 祖父。
  • 一对多 (1-to-N) : 一个老师有许多学生。

作者提供了理论证明，表明 MQuinE 保留了所有这些能力。

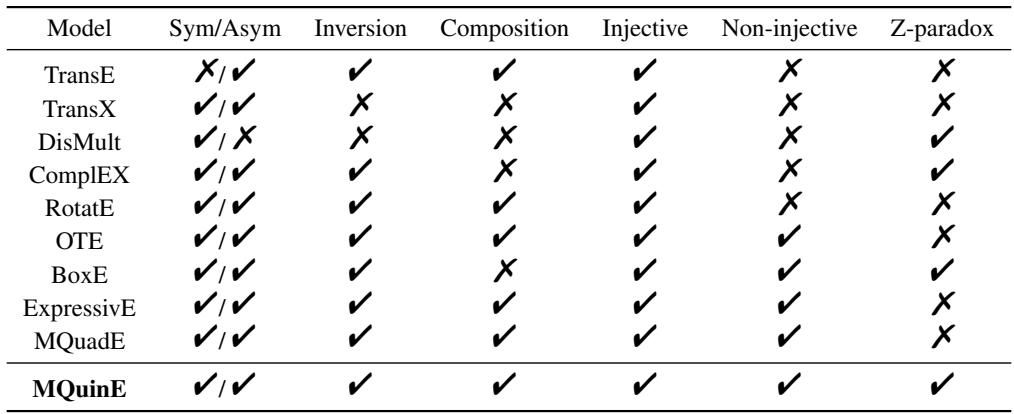
Table 3.1: The pattern modeling and inference abilities of several models.

如上表所示，MQuinE 是列出的模型中唯一涵盖所有类别且避免了 Z-悖论的模型。

训练策略: Z-采样

拥有更好的架构只是第一步。第二步是有效地训练它。标准的 KGE 训练使用“负采样”——取一个真实事实 \((h, r, t)\) 并将其破坏为 \((h, r, t')\) (一个虚假事实) ，以教导模型区分真伪。

然而，由于 Z-悖论是一个特定的结构陷阱，作者引入了 Z-采样 (Z-sampling) 。

该算法通过专门在训练数据中寻找 Z 模式来工作。

  1. 对于一个事实 \((h, r, t)\)，生成标准的负样本。
  2. 在图谱中寻找与这些负样本形成 Z 模式的其他实体。
  3. 将这些“Z-模式”三元组收集到一个集合 \(S_Z\) 中。

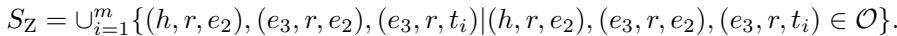
Definition of the Z-sample set

  1. 然后，模型被明确训练为拉大这些特定 Z 相关三元组的分数差距。这迫使模型利用那个新的交叉项矩阵 (\(\mathbf{R}^c\)) 的能力来解决歧义。

实验与结果

研究人员在标准基准上测试了 MQuinE: FB15k-237 (Freebase) 、WN18RR (WordNet) 和 YAGO3-10。

定义“困难”案例

为了证明 Z-悖论是真实的，他们不仅仅看平均准确率。他们根据“Z-值”对测试数据进行了分类——本质上是根据有多少 Z 模式定义了一个特定的测试事实。

  • 简单 (Easy) : 与 Z 结构关联不紧密的事实。
  • 困难 (Hard) : 深深嵌入 Z 结构中的事实，传统模型在此应该会失败。

Table 5.1: Case splitting description.

使用这种划分，他们分析了现有数据集的“Z-值”。他们发现，像 FB15k-237 这样的标准数据集中有很大一部分属于“困难”类别 (表 5.2) ，这意味着这不仅仅是一个理论上的边缘案例——它是一个普遍存在的问题。

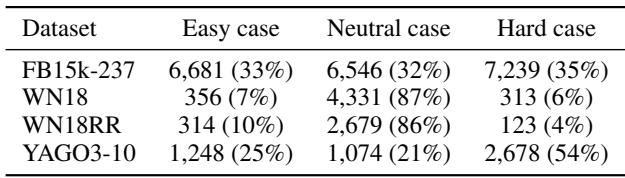
Table 5.2: Statistics of Z-patterns in the testing set.

Z-悖论案例的表现

结果令人震惊。在查看 困难 案例时，像 RotatE 和 TransE 这样的传统模型与简单案例相比，性能大幅下降。这从经验上证实了 Z-悖论确实损害了性能。

然而，MQuinE 坚守住了阵地。

Table 5.3: Hits@10 on easy, neutral, and hard cases of FB15k-237 and WN18RR.

查看上表中 FB15k-237 的 Hard 列。

  • RotatE: 39.7% 准确率 (Hits@10)。
  • MQuinE: 52.7% 准确率。

在受悖论影响最严重的数据点上，这是巨大的 13% 绝对提升 。 重要的是，MQuinE 在“简单”案例上也表现更好 (69.7% 对 67.7%) ，表明交叉项矩阵增加的复杂性也有助于提升通用表达能力。

整体表现

当在整个数据集上取平均值时 (不仅仅是困难案例) ，MQuinE 取得了最先进的结果。

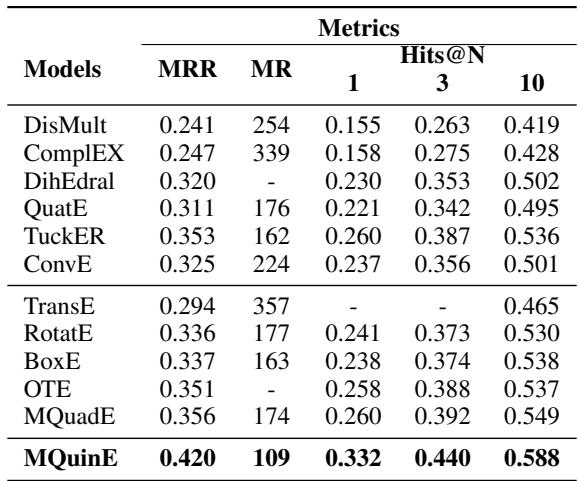
Table 5.4: Overall evaluation results on the FB15k-237 dataset.

在竞争激烈的 FB15k-237 数据集上，MQuinE 取得了 0.332 的 Hits@1 分数 , 显著高于 RotatE (0.241) 和 TuckER (0.260)。这表明“Z-悖论”可能多年来一直是一个限制 KGE 模型性能的隐形天花板。

在 YAGO3-10 数据集上也显示了类似的优势:

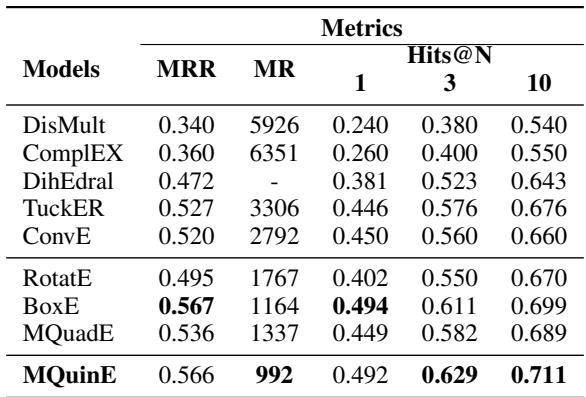
Table D.3: Overall evaluation results on the YAGO3-10 dataset.

Z-采样的影响

最后，作者检查了是否仅靠架构就足够了，或者“Z-采样”策略是否是必要的。

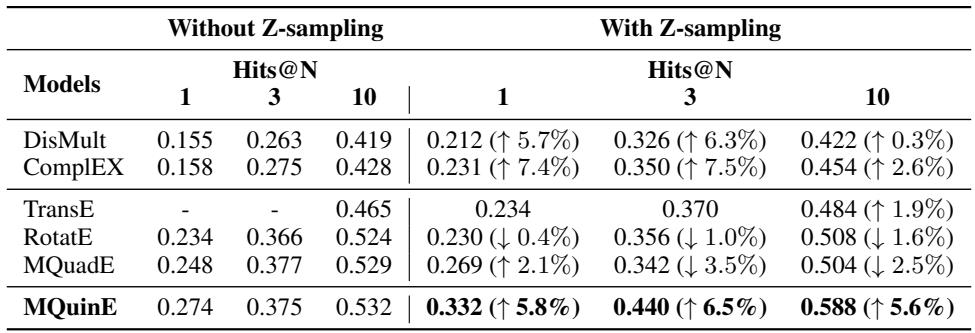
Table 5.5: Effect of Z-sampling on the FB15k-237 dataset.

结果显示了一种协同效应。虽然 Z-采样对某些模型 (如 DisMult) 有帮助，但实际上略微损害了 RotatE 的性能。然而，对于 MQuinE，Z-采样显著提升了性能 (Hits@1 从 27.4% 跃升至 33.2%) 。这证实了 MQuinE 的独特架构依赖于这种专门的采样来完全学习如何打破 Z-悖论的循环。

结论

“Z-悖论”是一个迷人的例子，展示了 AI 模型中的数学假设如何导致逻辑错误。通过假设关系可以建模为简单的平移 (\(h+r=t\)) ，我们无意中给模型植入了这样一个信念: 图谱中的每个“Z”形状都意味着一个闭环。

MQuinE 提供了一个稳健的解决方案。通过扩展关系的表示以包含交叉项 (\(\mathbf{HR}^c\mathbf{T}\)) ，它打破了束缚传统模型的线性链条。

  • 它在数学上被证明可以避免该悖论。
  • 它保留了模拟复杂关系模式的能力。
  • 它显著优于现有的基准模型，尤其是在困难的、易产生悖论的数据上。

对于知识图谱领域的学生和研究人员来说，MQuinE 强调了质疑嵌入底层几何假设的重要性。有时候，要跳出思维定势 (Think outside the box) ，你需要打破这个 Z。