在机器学习领域，尤其是自然语言处理 (NLP) 中，我们经常追求在基准测试中获得最高的准确率分数。但这台机器中潜藏着一个幽灵: 随机性 。

想象一下，你正在用非常有限的数据训练一个模型——也许是一个少样本分类任务。你运行实验并获得了 85% 的 F1 分数。你欣喜若狂。但是，当你更改了“随机种子” (控制数据洗牌或权重初始化的简单整数) 并再次运行它时，分数掉到了 60%。

这种现象就是机器学习中的“蝴蝶效应”。微小的、非确定性的选择 (随机性因子) 可能会导致性能的巨大偏差。这是一个已知的问题，但新的研究表明，我们以前对它的诊断可能是错误的。

在论文 “On Sensitivity of Learning with Limited Labelled Data to the Effects of Randomness” 中，研究人员 Branislav Pecher、Ivan Srba 和 Maria Bielikova 指出，以往关于随机性的研究存在缺陷，因为它们忽略了不同因子之间的交互作用 。

在这篇深度文章中，我们将探索他们用于理清这些交互作用的新颖方法，并揭示在有限数据下训练模型时，究竟哪些选择才是至关重要的。

问题所在: 当“最先进”仅仅是因为运气好

有限标签数据学习 (Learning with limited labelled data) ——涵盖上下文学习 (In-Context Learning, ICL) 、微调 (fine-tuning) 和元学习 (meta-learning) 的一个总称——以其不稳定性而臭名昭著。

先前的研究已经确定了导致这种不稳定的几个“随机性因子”:

  1. 数据顺序 (Data Order) : 模型看到示例的顺序。
  2. 样本选择 (Sample Choice) : 哪些具体示例被选中用于少样本提示或训练集。
  3. 模型初始化 (Model Initialization) : 神经网络的随机初始权重。
  4. 数据划分 (Data Split) : 可用数据如何划分为训练集和验证集。

由这些因子引起的变异可能比一个新的“最先进” (state-of-the-art) 架构所带来的提升还要大。这导致了可复现性危机。如果一个模型仅仅是因为碰到了一个幸运的随机种子才击败了基准，我们真的取得进步了吗？

现有调查方法的缺陷

为了了解哪些因子破坏了稳定性，研究人员通常使用以下两种策略之一:

  1. 随机策略 (The Random Strategy) : 同时改变所有因素。这虽然捕捉到了总方差，但无法查明是哪一个因子导致了性能下降。
  2. 固定策略 (The Fixed Strategy) : 固定除一个因子外的所有因子 (例如，固定数据顺序和初始化，但改变样本选择) 。

这篇论文的作者认为固定策略具有误导性。为什么？因为随机性因子之间存在交互作用 。

例如，上下文学习 (ICL) 曾被普遍认为对提示中样本的顺序非常敏感。然而，后来的研究发现，如果智能地而不是随机地选择样本，这种敏感性就会消失。这意味着存在交互作用: “数据顺序”的重要性在很大程度上取决于“样本选择”。如果你只是孤立地研究它们，你会得到不一致、相互矛盾的结果。

一种新方法: 在考虑交互作用的情况下调查随机性

这篇论文的核心贡献是一个严格的数学框架和算法，旨在隔离一个随机性因子的影响，同时在统计上解释其他因子的影响。

该方法围绕三个关键概念展开:

  1. 调查 (Investigation) : 改变我们想要研究的特定因子。
  2. 缓解 (Mitigation) : 系统地改变其他因子以平均消除它们的噪音。
  3. 黄金模型 (The Golden Model) : 一个代表当所有因素都随机时的总方差的基准。

让我们一步步分解这是如何工作的。

第一步: 定义配置

首先，我们定义所有随机性因子 (RF) 的集合。假设我们要调查因子 \(i\) (例如，数据顺序) 。我们需要区分我们要观察的因子和我们需要缓解的“背景”因子。

作者定义了一个缓解因子配置 (Mitigated Factor Configuration, \(MFC_i\)) 。 这是其他因子的所有可能组合的集合。

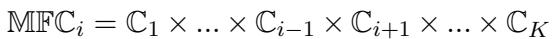
描述缓解因子配置集合的公式。

在这个公式中:

  • \(\mathbb{C}_i\) 是我们要调查的因子的配置集合。
  • 该等式代表所有其他配置集合 (\(\mathbb{C}_1\) 到 \(\mathbb{C}_K\)，排除 \(i\)) 的笛卡尔积。

第二步: 调查循环

为了分析因子 \(i\)，该算法执行一个嵌套循环。

  1. 它将“背景”因子固定在一个特定的配置 (\(m\)) 。
  2. 然后在所有可能性中改变被调查的因子 \(n\)。
  3. 它测量模型的性能 (\(r_{m,n}\)) 。

这生成了一个结果矩阵，如下表所示:

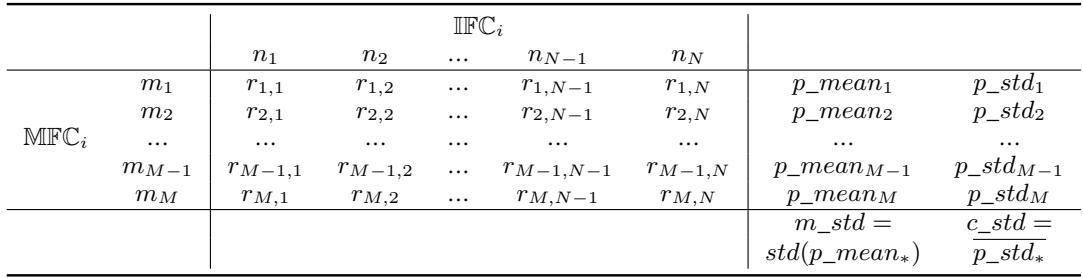
表 2: 方法的结果矩阵可视化。行代表缓解运行，列代表调查运行。

理解表格:

  • 列 (\(n_1, n_2...\)): 这些是你正在研究的因子的不同状态 (例如，数据顺序的不同排列) 。
  • 行 (\(m_1, m_2...\)): 这些是其余环境的不同“固定”状态 (例如，特定的数据划分和模型初始化) 。

第三步: 计算贡献偏差与缓解偏差

这是数学上最巧妙的地方。作者计算了两种不同类型的标准差，以便从噪声中分离出信号。

  1. 贡献标准差 (Contributed Standard Deviation, \(c\_std\)) : 看上面表格中的单一行。该行中的数值变化 (\(p\_std_m\)) 告诉我们，当其他一切保持不变时，由于被调查因子导致的性能变化有多大。作者计算每一行 (每个背景配置) 的这个值并求平均。这代表了因子 \(i\) 的“纯粹”影响。

  2. 缓解标准差 (Mitigated Standard Deviation, \(m\_std\)) : 看右边的 \(p\_mean\) 列。这里的每个值是特定背景配置下的平均性能。如果我们计算这些平均值的标准差，我们就得到了 \(m\_std\)。这个数字告诉我们，由于所有其他背景因子的交互作用，性能波动了多少。

第四步: 重要性评分

最后，为了确定一个因子是否真的重要，将其与黄金模型进行比较。黄金模型是通过同时改变所有因子来训练的。其标准差 (\(gm\_std\)) 代表了系统的“彻底混乱”或总不稳定性。

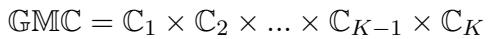
描述黄金模型配置集合的公式。

重要性评分 (Importance Score) 的计算公式为:

\[ \text{Importance} = \frac{c\_std - m\_std}{gm\_std} \]
  • 解释: 如果分数大于 0 , 则该因子是显著的。它对变异的贡献超过了所有其他因子的总和。如果它很低或为负，则不稳定性实际上来自其他因子的交互作用，而不是你正在调查的那个因子。

实验结果: 打破迷思

作者将这种方法应用于三种主要范式: 上下文学习 (使用 Flan-T5, LLaMA-2, Mistral, Zephyr 等模型) 、微调 (BERT, RoBERTa) 和元学习。他们在 7 个数据集上进行了测试，包括 GLUE 任务和像 AG News 和 DB-Pedia 这样的多分类任务。

当他们理清交互作用后，发现了以下结果。

1. 上下文学习中的“数据顺序”迷思

NLP 社区普遍认为上下文学习 (ICL) 对提示中示例的顺序极其敏感。

然而，当作者应用他们的方法时，他们发现数据顺序对于二分类任务上的 ICL 并不始终重要 。 当正确考虑交互作用后，归因于顺序的“不稳定性”实际上很大程度上是由样本选择 (具体选择了哪些示例) 驱动的。

下图总结了不同模型和数据集的重要性评分。

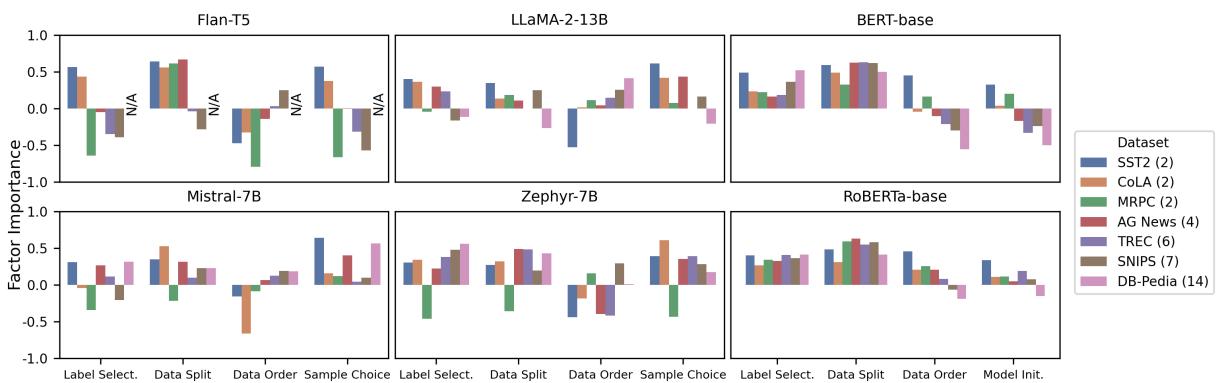
图 1: 考虑交互作用后，不同模型和数据集中随机性因子的重要性。

图 1 的关键要点:

  • 样本选择 (最右侧 Sample Choice) : 注意 ICL 模型 (上排) 中样本选择通常具有较高的正向条形图。这是主导因素。
  • 数据顺序 (右二 Data Order) : 对于二分类数据集 (如 SST2，用浅色表示) ，重要性通常为负或很低。然而，看那些深色的条形 (代表 DB-Pedia 等多分类数据集) 。随着类别数量的增加，数据顺序确实再次变得重要。
  • 微调 (下排) : 对于 BERT 和 RoBERTa，情况有所不同。它们对标签选择 (Label Selection) 和数据划分 (Data Split) 高度敏感，但对模型初始化不太敏感 (二分类任务除外) 。

2. 系统性选择: 样本数量 (Shots) 和类别 (Classes)

作者假设“系统性选择”——我们有意识做出的决定，比如使用多少个样本 (shots) 或预测多少个类别——会改变随机性的格局。

增加样本数量能稳定模型吗?

我们通常假设提供更多示例 (10-shot vs 2-shot) 会减少方差。结果显示了一个细微差别:

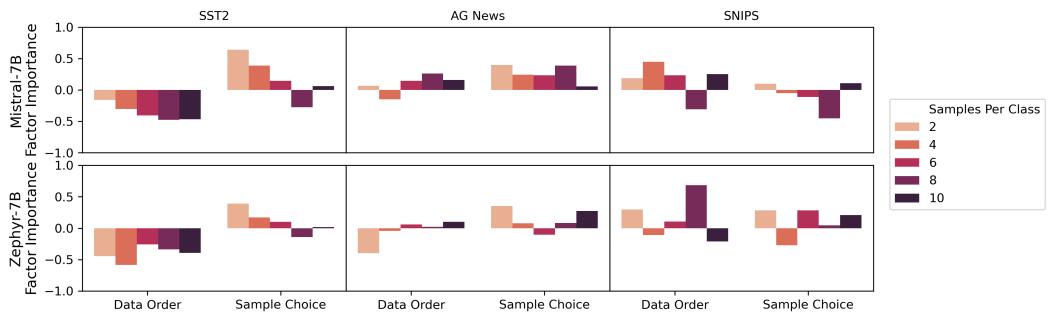
图 2: 热力图显示随着每类样本数增加，因子重要性的变化。

在图 2 中，我们可以看到:

  • 样本选择 (右列) : 随着样本数量 (每类样本数) 的增加 (从浅橙色到黑色条形) ，样本选择的重要性降低 。 这是合理的——选中 10 个糟糕示例在统计上比选中 1 个糟糕示例要难。
  • 数据顺序 (左列) : 令人惊讶的是，增加样本数量并不能持续降低对数据顺序的敏感性。模型对 10 个示例的糟糕排序的困惑程度与对 2 个示例一样。

3. 提示格式的影响

也许最引人注目的发现涉及提示模板本身。研究人员测试了一个“优化后”的提示与三个“极简”提示格式 (例如，仅仅是 “Sentiment: [Output]” 对比 “Determine the sentiment of the sentence…”) 。

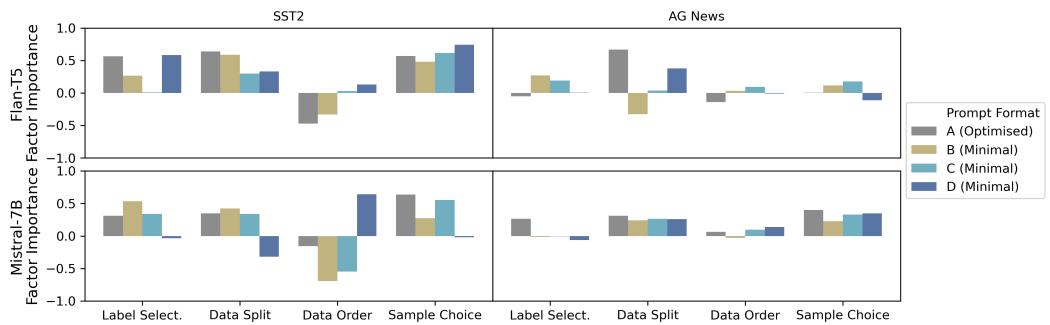
图 3: 提示格式对随机性因子重要性的影响。

图 3 的观察结果:

  • 对格式的敏感性: 看 Flan-T5 模型 (左侧) 。重要性评分随着格式 (A, B, C, D) 的不同而剧烈波动。极简格式通常会激增对随机性的敏感度。
  • 模型大小很重要: 较大的模型 Mistral-7B (右侧) 要稳健得多。条形图在不同提示格式下相对稳定。这表明经过指令微调的大型模型更好地内化了任务定义，并且不太依赖提示的具体措辞来稳定其随机性。

4. 元学习的发现

最后，作者调查了元学习方法 (如 MAML 和 Reptile) 。

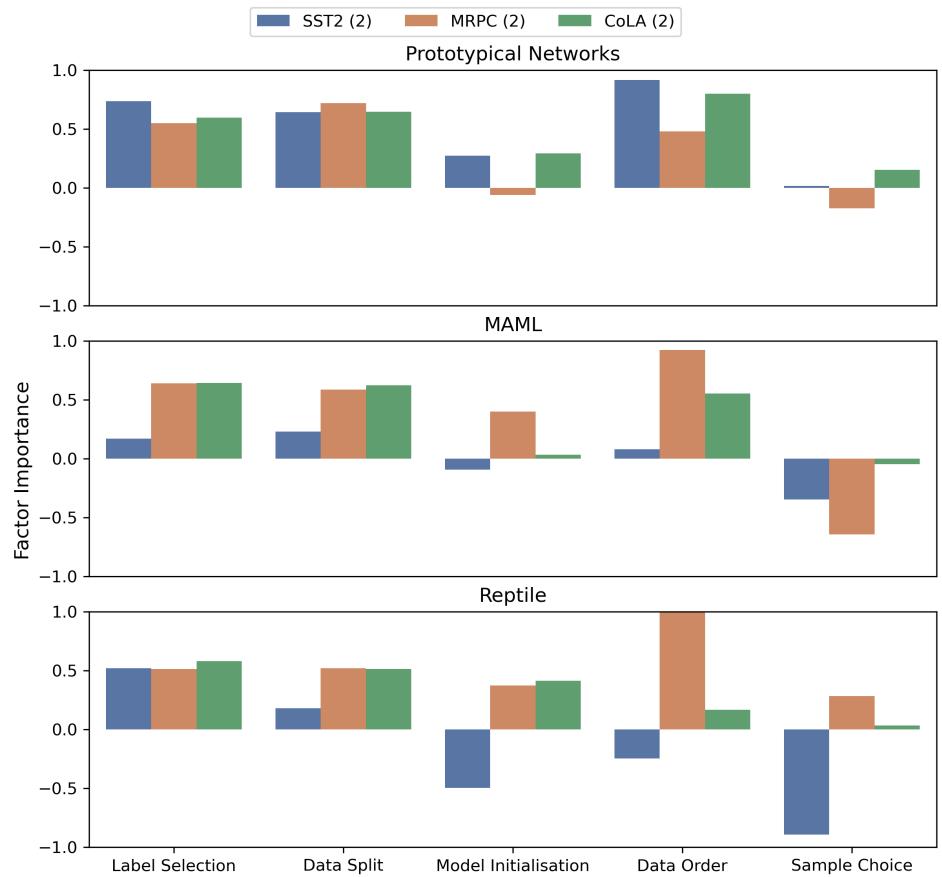
图 4: 元学习中随机性因子的重要性。

对于二分类数据集上的元学习, 数据顺序 (特别是任务/批次的顺序) 占据主导地位。它始终是最重要的因素，重要性评分通常达到 1.0 (贡献了几乎所有的偏差) 。这对于训练元学习算法的研究人员来说是一个至关重要的见解: 你如何打乱任务顺序比其他任何事情都重要。

结论与启示

这项研究为 NLP 社区提供了一个重要的“现实检验”。它强调了我们在少样本学习中观察到的不稳定性并不是铁板一块——它是一个由相互作用的因子组成的复杂网络。

给学生和从业者的关键要点:

  1. 不要相信简单的标准差: 如果你读到一篇论文声称“方法 X 对随机种子具有鲁棒性”，请检查他们是如何测试的。他们是否只改变了种子而固定了数据划分？如果是这样，他们可能低估了真实的方差。
  2. 在 ICL 中优先考虑样本选择: 如果你正在使用上下文学习构建应用程序 (如 GPT-4) ，花时间在如何选择少样本示例 (基于检索的选择) 上，比担心它们的顺序 (除非你有许多类别) 能带来更好的稳定性回报。
  3. 背景很重要: 一个对二分类任务致命的随机性因子，对于多分类任务可能微不足道，反之亦然。
  4. 使用该方法: Pecher 等人提出的算法 (调查-缓解-比较) 为诚实、可复现地报告模型稳定性提供了蓝图。

随着模型变得越来越大且不透明，理解随机性的“幽灵”变得愈发重要。通过剖析这些交互作用，我们将从依靠运气的“炼金术”，走向理解元素属性的“化学”。