引言

想象一下，你有一本内容精彩的百科全书，但它是在 2021 年印刷的。它知道那时的美国总统是谁，但对当前的时事、新的科学发现或书中错误的修正一无所知。这正是我们面对大型语言模型 (LLM) 时所处的困境。它们是互联网在特定时间点的静态快照。

当一个 LLM 产生“幻觉”或依赖过时信息时，我们的第一直觉可能是重新训练它。但是，重新训练像 GPT-J 或 Llama-2 这样庞大的模型，在时间和计算成本上都是天文数字。这催生了 模型编辑 (Model Editing) 领域——即在不破坏模型通用能力的前提下，对特定事实进行“手术式”的更新。

然而，现有的编辑方法面临着严峻的现实考验。大多数方法在单批次编辑 (例如，一次性修复 100 个事实) 时表现良好，但在尝试连续编辑 (例如，今天修复 10 个事实，明天修复 50 个，下周修复 200 个) 时就会崩溃。它们要么遭受“灾难性遗忘” (学习新知识导致遗忘旧知识) ，要么需要无限增长的大型外部存储库，要么需要训练复杂的“元网络”。

CoachHooK 应运而生。

在论文 “Consecutive Batch Model Editing with HooK Layers” 中，研究人员提出了一种支持 连续批量编辑 (Consecutive Batch Editing) 的新颖方法。它对内存友好，无需重新训练，并且在无缝整合新事实的同时保护模型的原始知识。在这篇文章中，我们将解构 CoachHooK 的工作原理，其更新机制背后的数学原理，以及为什么“Hook 层”是 LLM 可持续维护的秘密武器。

背景: 编辑领域的现状

要欣赏 CoachHooK，我们首先必须了解问题的约束条件。模型编辑不仅仅是改变一个预测；它是关于 可靠地 改变预测，确保改变具有泛化性 (重述提示词仍然有效) ，并确保 局部性 (不相关的知识不受破坏) 。

我们可以将编辑场景的难度分为三个级别:

1. 单样本与批量编辑 (Single Instance & Batch Editing) 标准的批量编辑试图最小化特定一组输入 \(\mathcal{X}_t\) 和目标 \(y_t\) 的误差。目标是找到满足新事实的新参数 \(\theta'\)。

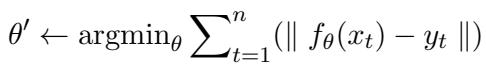
展示批量编辑目标函数的公式 3

2. 序列编辑 (Sequential Editing) 这更难。在这里，编辑是一个接一个发生的。模型必须针对事实 A 更新自身，然后是事实 B，接着是事实 C，随时间累积变化。

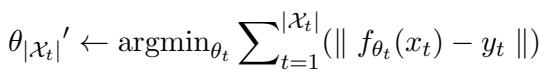
展示序列编辑目标函数的公式 4

3. 连续批量编辑 (CoachHooK 的目标) 这是最实用也是最困难的场景。我们希望在多个连续步骤中有效地 分批 更新模型。我们可能今天有一批 10 个编辑 (步骤 1) ，明天有一批 50 个编辑 (步骤 2) 。模型需要在不忘记前几批次或原始预训练数据的情况下整合新批次。

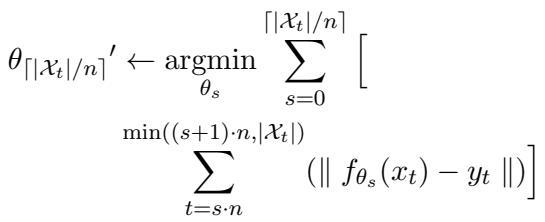
定义连续批量编辑目标的公式 5

大多数现有方法都在这里失败了。直接修改权重的方法往往会随时间迅速退化。使用外部存储器 (如修正数据库) 的方法随着添加更多编辑会变得越来越慢且笨重。CoachHooK 旨在通过保持原始权重冻结并使用轻量级、大小恒定的“Hook 层”来处理变化，从而解决这个问题。

CoachHooK 方法

CoachHooK 基于这样一个原则运作: Transformer 中的前馈网络 (FFN) 充当 键值记忆 (Key-Value Memories) 。 层的输入是一个“键 (Key)”，输出是一个“值 (Value)”。要编辑一个事实，我们本质上是想将一个特定的键 (代表“英国首相”) 与一个新的值 (“Rishi Sunak”而不是“Boris Johnson”) 关联起来。

该方法有三大支柱:

  1. 连续批量更新机制: 用于计算权重更新的数学方法。
  2. Hook 层 (The Hook Layer): 存储这些更新的架构组件。
  3. 局部编辑范围识别: 决定 何时 使用 Hook 层的逻辑。

1. 连续批量更新机制

研究人员建立在 MEMIT (Mass-Editing Memory in a Transformer) 方法的基础上，但将其扩展到了连续场景。

让我们看看某一层的权重 \(W_0\)。在预训练模型中，我们假设 \(W_0\) 使用最小二乘目标有效地将现有的键 (\(K_0\)) 映射到现有的值 (\(V_0\)):

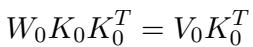
公式 10 展示权重、键和值之间的关系

当我们想要执行 连续 编辑时，我们不仅仅是为当前批次求解。我们要为一个权重 \(\hat{W}_1\) 求解，该权重既要尊重 新 的键/值批次 (\(K_2, V_2\))，又要保留 之前编辑过 的键/值 (\(K_1, V_1\))。

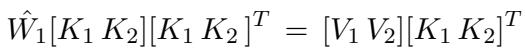
公式 12 展示了针对先前和新编辑的组合优化

这看起来很标准，但有一个转折。我们将 \(\Delta\) 定义为所需的权重 变化。通过展开线性代数公式，研究人员推导出了 \(\Delta\) 的公式，该公式考虑了残差 (\(R\)) 和目前为止所有键的累积协方差 (\(C_{accu}\))。

权重更新 \(\Delta\) 的公式为:

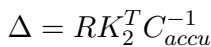
公式 13 展示 Delta 的计算

这里:

  • \(R = (V_2 - W_1 K_2)\) 是 残差 (residual error) 。 它代表了我们 希望 模型输出的内容与模型在给定最新权重的情况下当前输出的内容之间的差异。
  • \(C_{accu}\) 是键的累积。它确保更新相对于先前记忆的“强度”进行正确缩放。

这个数学基础确保了当我们计算新的更新时，我们在数学上考虑了编辑的历史，从而最大限度地减少了对先前知识的破坏。

2. Hook 层架构

如果我们反复修改原始模型权重 \(W\)，模型最终会“崩溃”或偏离其原始分布太远。为了防止这种情况，CoachHooK 引入了 Hook 层 。

可以将 Hook 层想象为特定 Transformer 层之上的透明覆盖层。

  • 它拥有自己的一组权重，从原始模型初始化而来。
  • 它充当一个开关。对于大多数输入，它让原始模型工作。
  • 对于特定的“已编辑”输入，它拦截数据并提供修正后的输出。

该架构涉及这些 Hook 的两种状态:

  1. 临时 Hook 层 (Temporary Hook Layer): 在计算更新 期间 使用，用于基于最新状态计算梯度和残差。
  2. 验证 Hook 层 (Validated Hook Layer): “生产”状态。它存储编辑步骤后的最终权重。

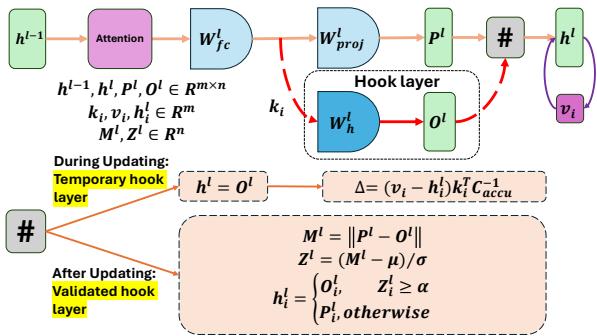
图 1: 带有 Hook 层的单层更新

如上图 图 1 所示，过程非常优雅。

  1. 输入 \(h^l\) 进来。
  2. 系统计算两个输出: \(P^l\) (来自原始冻结权重 \(W_{fc}\)) 和 \(O^l\) (来自 Hook 权重 \(W_h\)) 。
  3. 它计算两者之间的差异 (范数) 。
  4. 根据这个差异，它决定是输出 \(O^l\) (已编辑的知识) 还是 \(P^l\) (原始知识) 。

至关重要的是, Hook 层的内存大小不会增长 。 它保持固定的矩阵大小 (与其作用的层相同) 。你不需要存储不断增长的示例数据库；知识被压缩进了 Hook 权重 \(W_h\) 中。

3. 局部编辑范围识别 (“开关”)

模型如何知道何时使用 Hook 层的输出，何时忽略它？这就是 局部编辑范围识别 (Local Editing Scope Identification) 。

研究人员发现了一个迷人的特性: 离群值检测 (Outlier Detection) 。 如果一个键 \(k_i\) 在 Hook 权重 \(W_h\) 中被更新了，输出 \(W_h k_i\) 将与原始输出 \(W_0 k_i\) 有显著不同。 如果一个键 \(k_j\) 没有 被编辑，输出可能会非常相似。

因此，我们可以通过查看差异向量 \(M^l\) 的幅度来检测输入是否落入“编辑范围”:

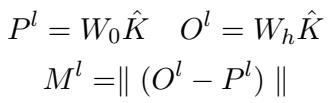
公式 17 展示差异向量幅度 M 的计算

然后我们可以将此幅度标准化为 Z-score (Z 分数，一种衡量数据点距离平均值多远的统计量) 。如果 Z-score 超过动态阈值 \(\alpha\)，我们假设输入与已编辑的事实相关，并换入 Hook 层的输出。

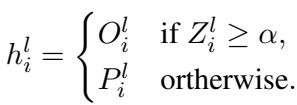
公式 19 展示基于 Z-score 交换输出的决策规则

这种方法有效地过滤掉了不相关的输入 (保持局部性) ，同时捕获了已编辑的输入 (确保可靠性) 。

阈值 \(\alpha\) 不是固定的；它是动态适应的。它从一个预设值开始，随着连续编辑的发生而收紧，以确保范围不会漂移得太宽。

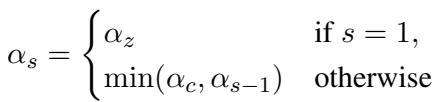
公式 20 展示 Alpha 的动态更新规则

4. 多层扩展

单层可能不足以捕获复杂的编辑，或者可能无法正确检测范围。CoachHooK 将此逻辑迭代地应用于多个层。

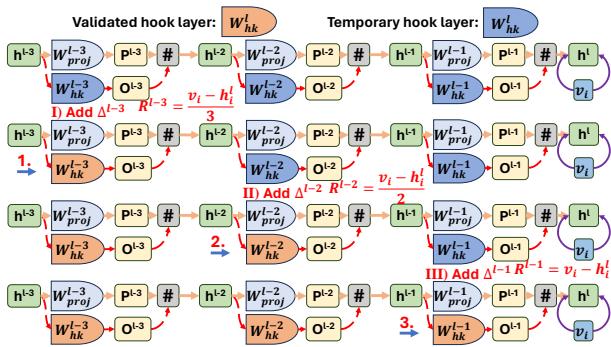
图 2: 带有 Hook 层的前层更新

如 图 2 所示，残差 (所需的修正) 分布在多个层上。系统更新第 1 层，根据该更新重新计算下一层的残差，然后更新第 2 层，依此类推。这种“层级递增迭代方式”确保了稳健的更新，使其在推理过程中更难被“遗漏”。

实验与结果

研究人员使用两个标准数据集将 CoachHooK 与 MEMIT、MEND、SERAC 和 LoRA 等强基线进行了评估:

  • ZsRE: 问答数据集。
  • COUNTERFACT: 一个具有挑战性的数据集，用于检查反事实更新 (例如，强迫模型相信埃菲尔铁塔在罗马) 。

单轮批量编辑

首先，他们测试了简单的单批次 (例如，只有一轮编辑) 。

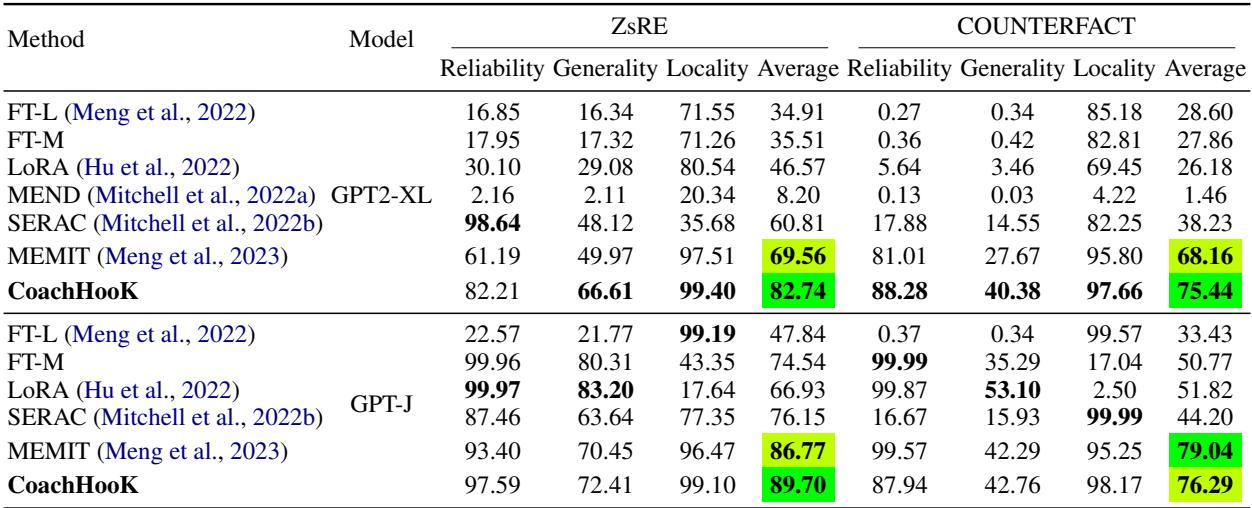
表 1: 单轮批量编辑结果

如 表 1 所示，CoachHooK (最后一行) 取得了优异的结果，特别是在 GPT2-XL 上的 泛化性 (Generality) (处理重述提示词的能力) 方面，同时保持了近乎完美的 局部性 (Locality) (99.40)。

连续批量编辑

这是重头戏。模型经受了连续的编辑流 (总共 1,000 个样本，分批次进行) 。

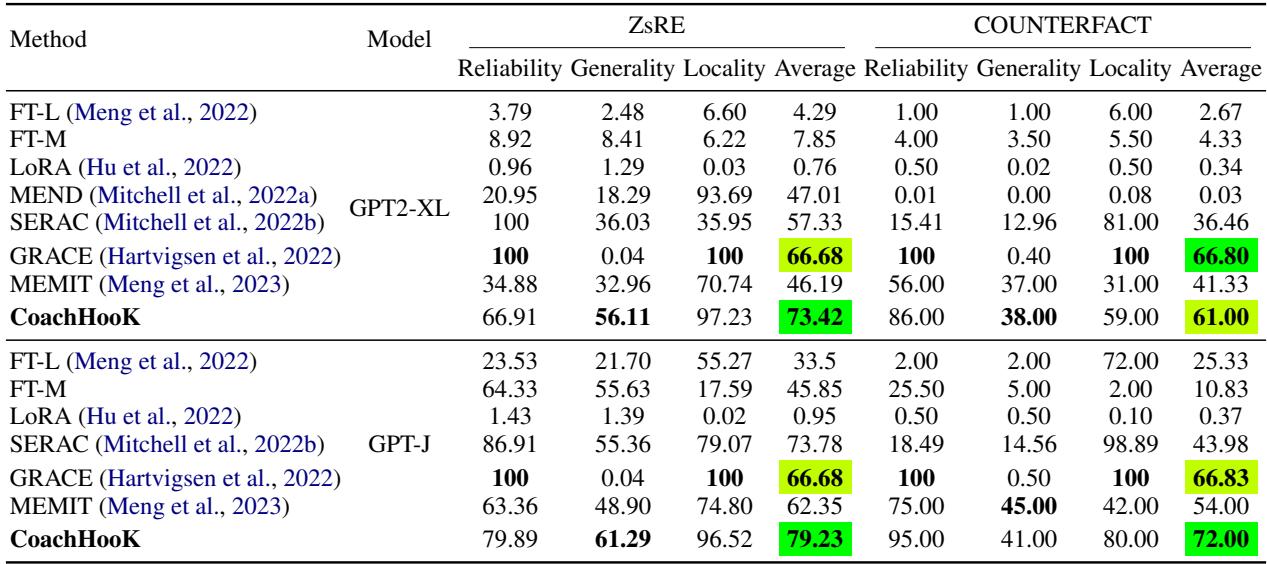
表 2: 连续批量编辑结果

表 2 揭示了 CoachHooK 的实力。

  • MEMIT (领先的基线) 从单轮切换到连续设置时，性能显著下降 (ZsRE 上的可靠性降至 34.88) 。
  • CoachHooK 保持了高可靠性 (56.11)，并且在泛化性方面比 GRACE 等方法有巨大的提升。
  • GRACE 具有很高的可靠性，但泛化性基本为零 (0.04)，这意味着它记住了特定的句子，但如果你换一种方式提问就会失败。CoachHooK 解决了这个死记硬背的问题。

为什么它有效？ (消融实验)

“Hook 层”是必须的吗？还是仅仅靠数学公式就足够了？

研究人员进行了一项消融研究，对比了:

  1. MEMIT (标准) 。
  2. 不带 Hook 层的 CoachHooK (仅将数学公式应用于原始权重) 。
  3. CoachHooK (完整版) 。

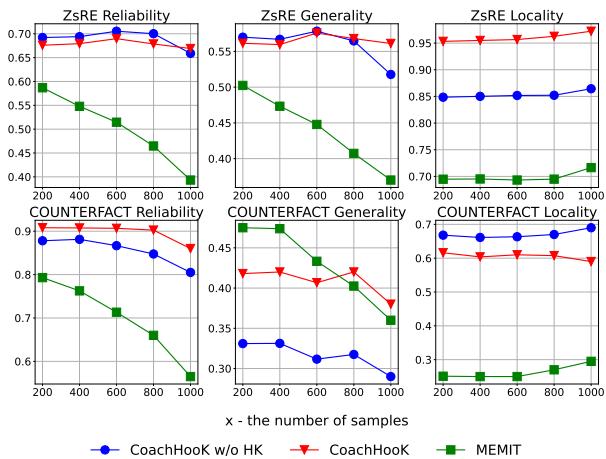
图 4: 比较带与不带 Hook 的 CoachHooK 的消融研究

图 4 (上图) 显示了 1,000 个样本的结果。

  • 红色三角形 (CoachHooK): 始终表现最好。
  • 蓝色圆形 (无 Hook): 表现优于 MEMIT，证明推导出的更新数学公式是合理的。
  • 绿色正方形 (MEMIT): 退化最快。

红线和蓝线之间的差距证明了 Hook 层架构 特别有助于在长序列编辑中稳定模型，防止通常会破坏局部性的“漂移”。

验证范围检测

人们可能会问: Z-score 真的是检测已编辑事实的好方法吗？

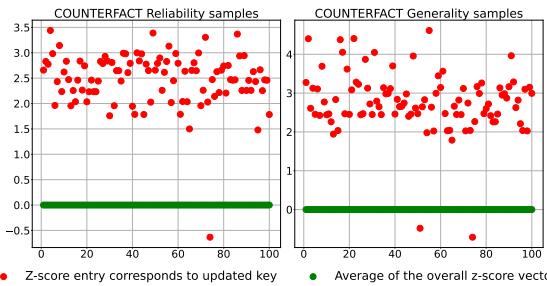
图 3: 已更新键的 Z-score 与平均值的差异

图 3 提供了经验证明。红点 (已更新的键) 始终显示出比绿线 (平均/未受影响的键) 高得多的 Z-score。这种清晰的分离使得简单的阈值机制 (\(\alpha\)) 能够在原始模型和 Hook 层之间准确切换。

结论与启示

“CoachHooK” 论文在大型语言模型的生命周期管理方面迈出了重要一步。通过摆脱昂贵的重新训练和静态编辑方法，它为 连续批量编辑 提供了一条可持续的路径。

主要收获:

  1. 内存效率: 与将每个编辑存储在数据库中的方法不同，CoachHooK 将更新压缩为固定大小的 Hook 层。
  2. 稳定性: “原始权重”和“Hook 权重”的分离防止了困扰标准微调的灾难性遗忘。
  3. 范围智能: 使用离群值检测 (Z-score) 提供了一种简单但在统计上合理的方法来确定编辑 何时 应该生效。

随着 LLM 越来越融入日常生活，持续更新它们的能力——在无需全面重新训练的情况下修正错误和添加新闻——将变得至关重要。CoachHooK 为我们提供了一个蓝图，让我们了解如何在不耗尽资金或破坏模型的情况下保持 AI 助手的最新状态。