这是现代人工智能最大的讽刺之一: 像 GPT-4 这样的大型语言模型 (LLM) 可以像莎士比亚那样写十四行诗，调试复杂的 Python 代码，并通过律师资格考试，但在被要求计算两个三位数的乘法时却经常栽跟头。

对于探索 Transformer 架构的学生和研究人员来说，这种行为可能令人困惑。计算机本质上就是计算器。为什么我们构建的最先进的“计算机大脑”在基础算术上表现得如此糟糕？

答案在于这些模型读取和生成文本的方式。它们按顺序逐个 token (标记) 地处理信息。虽然这种方式对于英语句子来说非常完美，但对于数字来说却存在根本性的缺陷。来自 IBM 和 MIT 的研究人员最近发表了一篇题为 “Numerologic: Number Encoding for Enhanced LLMs’ Numerical Reasoning” (NumeroLogic: 用于增强 LLM 数值推理的数字编码) 的论文，针对这个问题提出了一个令人着迷且看似简单的解决方案。

在这篇文章中，我们将剖析为什么 LLM 难以处理数学问题，“NumeroLogic” 编码如何通过借用人类认知的概念来解决这个问题，并查看表明该方法不仅能增强算术能力，还能增强通用语言理解能力的实证证据。

问题所在: 没有位值概念的阅读

要理解解决方案，我们必须首先理解瓶颈所在。LLM 是因果 (causal) 模型。它们从左到右读取文本，只关注之前的 token。

想象一下，你正在逐位读取一个数字，但不允许你看后面。你看到了数字 1。 这个 1 代表一个个位数吗？它是 10 的开头吗？还是 1,000,000 的首位数字？

在你读完整个数字字符串之前，你无法知道那个数字的位值 (量级) 。然而，LLM 的内部表示 (embedding) 是逐个 token 更新的。当模型处理第一个数字时，它是处于一种模糊状态下进行的。它实际上不得不“猜测”这个量级。

图 1: 对于 LLM 来说，像人类一样从左到右以因果方式读取数字并非最佳选择。模型必须读到数字的最后几位才能推断出第一位数字的位值。为了解决这个问题，我们提出了“NumeroLogic”，这是一种在实际数字之前标明数字位数的数值格式。

如图 1 所示，老师纠正了学生，因为数字 1 暗示了某种量级，而一旦完整的等式显现出来，原本的推断就变成错误的了。标准的 LLM 也遭受着同样的缺乏预见性的困扰。

此外，流行的分词器 (如 BPE) 会随意地切割数字。数字 1234 可能是一个 token，而 1235 可能会被切分成 12 和 35。这种不一致性使得模型极难学习一致的算术规则。

解决方案: NumeroLogic

研究人员提出了一种称为 NumeroLogic 的方法。其核心假设很简单: 如果模型在读取数字之前就知道其长度，它就能立即知道每个数字的位值。

NumeroLogic 没有将数字“42”仅仅表示为“42”，而是将其重新格式化以包含一个指示其长度的前缀。

格式

该编码引入了特殊的 token 来构建数字结构:

  • <sn>: Start Number (数字开始)
  • <mn>: Mid Number (数字中间，即长度和数值的分隔符)
  • <en>: End Number (数字结束)

格式遵循以下模式: <sn> [位数计数] <mn> [实际数字] <en>

示例:

  1. 整数 (42):
  • 标准格式: 42
  • NumeroLogic: <sn>2<mn>42<en>
  • 解释: “我即将读取一个长度为 2 的数字。这个数字是 42。”
  1. 浮点数 (3.14):
  • 标准格式: 3.14
  • NumeroLogic: <sn>1.2<mn>3.14<en>
  • 解释: “我即将读取一个包含 1 位整数和 2 位小数的数字。这个数字是 3.14。”

输入与输出的双重机制

这种编码不仅仅帮助模型“阅读”。它从根本上改变了模型在生成时的“思考”方式。

1. 增强的输入表示 (位值)

当模型读取 token <sn>3<mn>123... 时，在它处理数字 1 时，它已经明确关注了长度 3。模型立即知道这个 1 处于百位上 (\(10^2\)) 。它不再需要猜测量级。

2. 隐式思维链 (CoT)

最强大的效果发生在模型生成答案时。如果你要求模型计算 \(25 + 25\)，它不能直接吐出数字。它必须首先预测答案的长度 。

模型实际上在思考: “我正在将两个 2 位数相加。结果很可能是 2 位数 (如 40) 或 3 位数 (如 105) 。鉴于输入是 25 和 25，结果长度为 2。”

通过迫使模型在生成数字 (50) 之前先预测长度前缀 (<sn>2<mn>) ，NumeroLogic 充当了一个内置的思维链 (CoT) 。 它强制在计算之前进行一个推理步骤——量级估计。

实现细节

对于想要复制或理解其背后工程原理的学生来说，实现起来出奇地轻量级。它不需要新的模型架构。

  1. 预处理: 一个正则表达式 (Regex) 函数会扫描文本，并在分词之前将所有数字转换为 NumeroLogic 格式。
  2. 词表扩展: 对于预训练模型 (如 Llama-2) ，特殊的 token (<sn>, <mn>, <en>) 被添加到词表中。嵌入层和最终输出层会调整大小以适应这些新 token。
  3. 微调: 模型在修改后的文本上进行训练 (或使用 LoRA - 低秩自适应进行微调) 。
  4. 后处理: 在推理过程中，生成的特殊 token 和长度前缀会使用正则去除，向用户返回干净的数字。

实验结果

研究人员在从头训练的小模型和大型预训练模型上都验证了这一假设。

1. 算术能力 (小模型)

他们从头开始在算术任务上训练了一个小型 Transformer (NanoGPT)。结果非常显著。

  • 加法: 准确率从 88.37% (普通文本) 跃升至 99.96% (NumeroLogic)。
  • 乘法: 准确率翻了一倍多，从 13.81% 提高到 28.94% 。

这证明了对于一个从零开始学习数学的模型来说，知道数字的长度是一个关键的归纳偏置。

2. 扩展 (Llama-2 7B)

团队随后将 NumeroLogic 应用于 Llama-2 7B，在涉及更大数字和浮点运算的算术任务上对其进行微调。

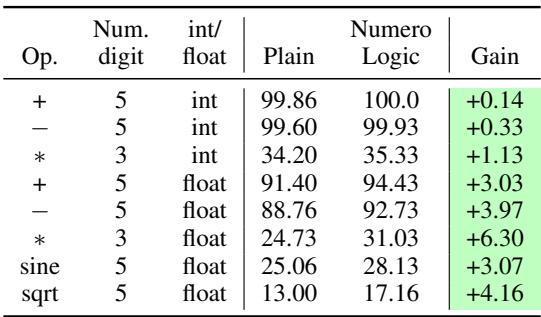
表 2: Llama2-7B 在 NumeroLogic 编码下的算术任务准确率。我们观察到，在所有性能尚未饱和的任务中，得益于 NumeroLogic 编码，都有显著的提升。

如上方的表 2 所示，收益是一致的。

  • 加法: 模型达到了完美的 100% 准确率。
  • 浮点运算: 注意 sine (正弦) 和 sqrt (平方根) 运算的改进。这对 LLM 来说是出了名的困难，因为它们需要高精度。NumeroLogic 在这里提供了 3% 到 4% 的提升。
  • 乘法: 即使是浮点数乘法 (3 位数) ，准确率也提高了超过 6% 。

3. 通用智能 (MMLU 基准测试)

人们可能会担心，用数字长度前缀填充文本会在非数学任务上混淆模型。为了测试这一点，研究人员使用 NumeroLogic 格式在通用网络文本上继续预训练 Llama-2，然后在 MMLU (Massive Multitask Language Understanding，大规模多任务语言理解) 基准上对其进行评估。

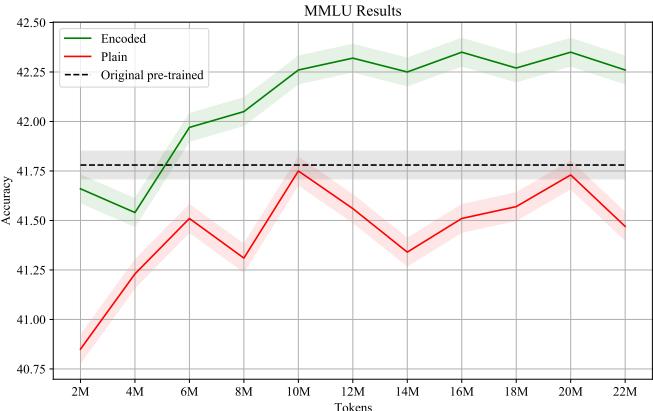
图 2: Llama2-7B 的 MMLU 准确率。在网络策划的文本 token 上继续进行自监督预训练时，当数字使用 NumeroLogic 编码时，有助于提高性能，超过了预训练模型或在相同文本上使用普通数字训练的模型。 表 4: 由于 NumeroLogic 编码导致的 MMLU 准确率变化，分为有数字和无数字的任务。带有数字的任务享受到更高的提升。

图 2 中的曲线揭示了一个令人惊讶的结果: 模型实际上变得更聪明了。

使用 NumeroLogic (绿线) 的表现始终优于普通文本训练 (红线) 。这表明更好的数值推理能力可以迁移到通用的语言理解中。

表 4 (图片右侧) 进一步细分了这一点。虽然没有数字的任务只看到了微小的收益 (+0.14%) ，但带有数字的任务看到了显著的跳跃 (+1.16%) 。

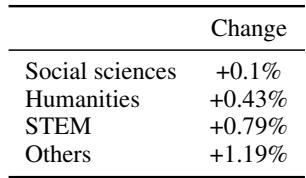
表 3: 不同领域任务中由于 NumeroLogic 编码导致的 MMLU 准确率变化。更有可能需要数值理解的 STEM 任务享有更高的提升。

表 3 按学科确认了这一趋势。 STEM 领域天然地严重依赖数字和逻辑，其提升幅度几乎是人文学科的两倍。这证实了该编码不仅仅是一个“数学把戏”——它提高了模型处理自然语言中量化信息的能力。

为什么它有效？消融实验

研究人员进行了几项消融实验，以查明 NumeroLogic 为什么有效。是因为输入上下文吗？是输出规划吗？还是仅仅因为我们要添加了更多的 token？

输入 vs 输出

他们尝试仅将编码应用于操作数 (输入数字) 或仅应用于结果 (输出数字) 。

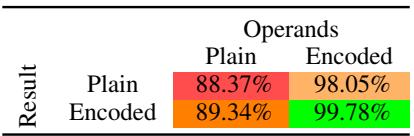
表 5: 测试编码等式的操作数与结果的效果。在 NanoGPT 的加法任务上进行测试。无论是编码操作数 (即输入理解) 还是编码结果 (即 CoT 效应) 都有积极效果，其中编码操作数的效果更强。同时编码操作数和结果能提供最佳性能。

表 5 给出了明确的答案: 两者都很重要，但结合起来是关键。

  • 仅编码操作数 (98.05%): 这有助于模型正确阅读问题 (位值) 。
  • 仅编码结果 (89.34%): 这迫使模型规划答案长度 (思维链) ，相比基线提供了小幅提升。
  • 两者都编码 (99.78%): 这释放了全部潜力。模型既能正确阅读，又能正确规划其输出。

替代编码方式

研究人员还检查了其他编码风格是否有效。例如，使用特定的 token 表示“3位数”，而不是通用的 <sn>3<mn> 格式。

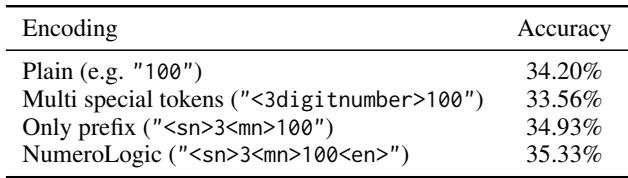
表 6: 不同替代编码方式在 3 位整数乘法上的表现。

如表 6 所示，使用“多重特殊 token” (为每个可能的长度设置一个唯一的 token) 实际上损害了性能 (33.56%) ，低于基线 (34.20%) 。这很可能是因为 token 变得太稀疏了——模型很少看到“15位数”的 token，所以学不好它。NumeroLogic 方法 (<sn>长度<mn>) 更优，因为代表长度的数字 (例如“3”) 是常见且模型很容易理解的。

仅仅是“更多计算”吗？

对思维链技术的一个常见批评是，它们只是给了模型更多的“时间” (token) 来计算。我们能否通过添加随机空白符来获得相同的效果？

表 7: 额外 token 的效果: 仅仅添加填充空白符没有帮助，并且与普通格式相当。在随机位置添加填充 token 的随机空白符方法 (Shen et al., 2023) 有帮助，但不如 NumeroLogic 有效。

表 7 平息了这一理论。

  • 空白符: 简单地用空格填充等式导致 24.37% 的准确率——比什么都不做还差。
  • 随机空白符: 一种涉及随机间隔 (以打破位置过拟合) 的先前技术达到了 27.76% 。
  • NumeroLogic: 达到了 31.03% 。

NumeroLogic 提供的特定语义信息——数字的计数——才是驱动性能提升的原因，而不仅仅是额外的 token 开销。

结论与启示

NumeroLogic 论文提供了一个令人信服的论点，即 LLM 在算术方面的局限性不一定是 Transformer 架构本身的局限性，而是我们如何表示数据的人为产物。

通过将数字视为从左到右读取的纯文本字符串，我们剥夺了模型对于数值素养至关重要的结构上下文 (位值) 。通过简单地前置长度——实际上是在说“这是一个 3 位数”——我们提供了模型准确处理数值所需的缺失上下文，以及正确生成数值所需的规划步骤。

对于学生和从业者来说，主要启示如下:

  1. 表示很重要: 你如何对数据进行分词和格式化，可能与模型架构一样重要。
  2. 规划是关键: 迫使模型在生成内容之前规划输出“结构”的技术 (如预测长度) 充当了强大的隐式推理步骤。
  3. 泛化: 如果从根本上在预训练数据中实施，特定领域 (如数学) 的改进可以渗透到通用性能 (如 STEM 推理) 中。

随着模型不断增长，像思维链这样的“事后”提示技巧很可能会像 NumeroLogic 演示的那样，直接整合到训练数据格式中。“智能”模型的未来可能始于教会在说话前先数数它们的数字位数。