随着大型语言模型 (LLM) 在自然语言处理领域占据主导地位，一个同样困难的次生问题随之出现: 我们该如何评估它们?

当 LLM 生成摘要、故事或一行对话时，很少有一个单一的“正确”答案。传统的指标如 BLEU 或 ROUGE 依赖于与参考文本的词重叠度，往往无法捕捉连贯性、创造力或有用性等细微差别。这导致了 LLM-as-a-judge (LLM 作为裁判) 的兴起，即我们使用更强的模型 (如 GPT-4 或 Llama-2-Chat) 来给其他模型的输出打分。

目前，这种评估的金标准是成对比较 (pairwise comparison) 。 我们不再要求模型“给这段文本打 1 到 10 分” (这种方式众所周知地不一致) ，而是问: “文本 A 和文本 B 哪个更好？”

然而，这其中有一个问题。如果你有 100 个候选回复需要排名，比较每一对回复需要近 10,000 次 API 调用。其成本呈二次方增长 (\(O(N^2)\)) 。对于大规模基准测试来说，这在成本上极其昂贵且速度缓慢。

在这篇文章中，我们将深入探讨剑桥大学 Liusie 等人的一篇研究论文，该论文提出了一种称为专家乘积 (Product of Experts，PoE) 的数学框架。这种方法使我们能够仅使用所有可能比较中的一小部分来准确地对文本进行排名——在保持与人类判断高度相关的同时节省计算资源。

直觉: 将比较视为“专家”

为了理解这个解决方案，我们需要首先重新审视我们看待问题的方式。

在标准的排名场景中，你有一组具有潜在“真实”分数的项目 (文本) 。当 LLM 比较文本 A 和文本 B 时，它会做出一个决定。传统上，我们将其视为一个二元结果: A 胜或 B 胜。然后我们将这些胜负结果输入到像 Bradley-Terry 模型 (类似于国际象棋中的 ELO 系统) 这样的算法中来估计分数。

但 LLM 提供给我们的不仅仅是二元决定。它们还提供概率 。 LLM 可能会说，“我有 90% 的把握 A 比 B 好”，或者“我有 51% 的把握 A 更好”。传统方法往往会丢弃这种丰富的不确定性信息，将其转化为硬性的“胜”或“负”。

这篇论文的作者提出了不同的观点: 将每一次成对比较视为一个独立的“专家”。

想象一屋子的专家。一位专家看了文本 A 和文本 B，给出了 A 比 B 好多少的概率分布。另一位专家看了文本 B 和文本 C。 专家乘积框架在数学上结合了所有这些独立的意见，以同时找到所有文本最可能的分数。

数学基础

形式上，假设我们要对 \(N\) 个候选文本进行排名。我们想找到它们的分数，表示为 \(s_{1:N}\)。我们要进行一组 \(K\) 次成对比较，\(\mathcal{C}_{1:K}\)。

给定比较结果，某组特定分数的概率可以通过将每个单独比较 (专家) 给出的概率相乘来建模。目标是找到使该概率最大化的分数:

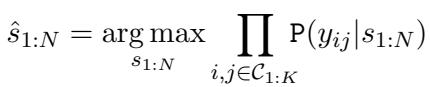
最大化给定比较下分数的概率的公式。

这里，\(\mathbb{P}(y_{ij} | s_{1:N})\) 是在给定分数的情况下观察到的结果的可能性。

在专家乘积 (PoE) 视角下，我们将此泛化。我们关注的不仅仅是二元结果 (\(y_{ij}\)) ，而是比较 \(C_k\) 提供的关于文本 \(i\) 和文本 \(j\) 之间分数差异的信息。

给定比较结果的分数概率定义为各个专家的乘积，并由常数 \(Z\) 归一化:

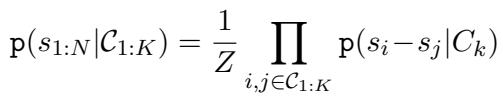
专家乘积公式。

这个等式是该框架的支柱。它的意思是: “这些分数为真的可能性，是每一次比较告诉我们的关于分数差异的信息的乘积。”

两类专家

该框架非常灵活——你可以为你的“专家”插入不同的数学模型。论文探讨了两种主要的变体。

1. 软 Bradley-Terry 专家

传统的 Bradley-Terry 模型使用 Sigmoid 函数 (\(\sigma\)) 根据分数差 (\(s_i - s_j\)) 来建模文本 \(i\) 击败文本 \(j\) 的概率。

作者将其扩展以处理 LLM 输出的软概率 (\(p_{ij}\)) 。如果 LLM 预测文本 \(i\) 更好的概率为 \(p_{ij}\)，则专家的似然函数变为:

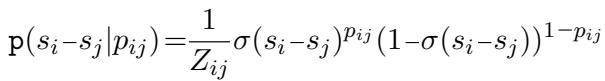
软 Bradley-Terry 专家公式。

这个模型很强大，但它有一个缺点: 找到最佳分数需要迭代优化算法 (如 Zermelo 算法) ，如果试图动态选择下一个最佳比较，重复计算的速度会很慢且计算量大。

2. 高斯专家 (破局者)

这是论文在效率方面做出重大贡献的地方。与其使用 Bradley-Terry 复杂的 Sigmoid 函数，如果我们要假设比较产生的信息遵循高斯 (正态) 分布会怎样？

如果 LLM 以概率 \(p_{ij}\) 说“A 比 B 好”，我们可以将其解释为分数差 \(s_i - s_j\) 上的高斯分布。

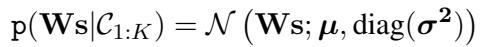
高斯专家公式。

这里，这个高斯分布的均值 (\(\mu\)) 和方差 (\(\sigma^2\)) 取决于 LLM 提供的概率 \(p_{ij}\)。

为什么要使用高斯分布？因为高斯分布的乘积仍然是高斯分布。 这使我们能够使用线性代数来找到分数的精确闭式解 , 而无需任何迭代循环。

比较结构可以用矩阵 \(\mathbf{W}\) 表示。对于项目 \(i\) 和项目 \(j\) 之间的比较，矩阵中的该行在索引 \(i\) 处为 \(+1\)，在索引 \(j\) 处为 \(-1\)。

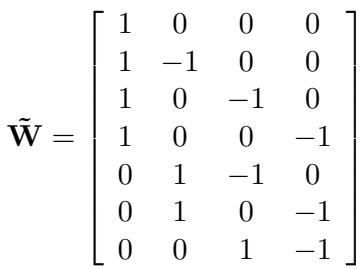
W 比较矩阵结构。

利用这种矩阵结构，论文推导出了最佳分数 \(\hat{s}\) 的优雅闭式解:

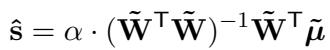
使用高斯专家的分数闭式解。

在这个公式中:

  • \(\mathbf{W}\) 是比较矩阵 (谁和谁进行了比较) 。
  • \(\tilde{\boldsymbol{\mu}}\) 是 LLM 概率预测的分数差异向量。
  • \(\alpha\) 是一个缩放因子。

这个公式允许系统在每次进行新比较后立即计算所有文本的最佳排名，这对效率至关重要。

验证假设

高斯专家假设“真实”的分数差异与 LLM 的预测概率呈线性关系。这在实际上是真的吗？

研究人员通过将 LLM 的预测概率与作为基准的真实人类评分进行对比来分析数据。

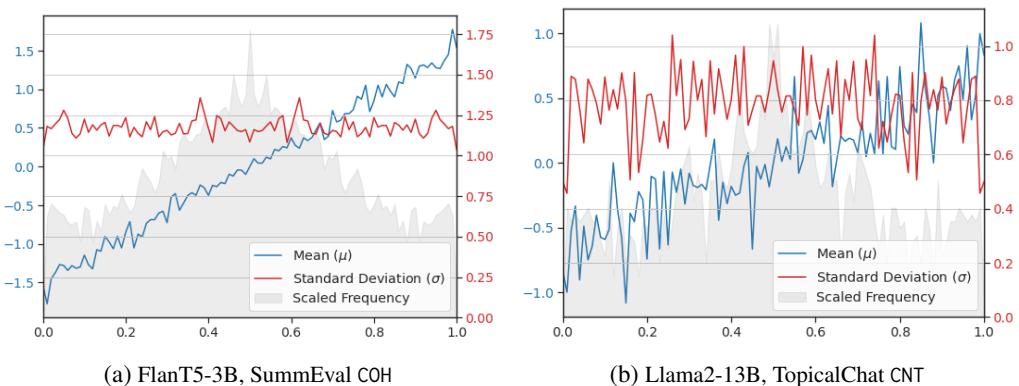
期望分数差异和方差与 LLM 概率的关系图。

如上面的 图 10 所示:

  1. 线性度 (蓝线) : LLM 概率 (x 轴) 与平均分数差异 (y 轴) 之间的关系惊人地呈线性。随着模型变得更加自信 (概率趋向于 1.0) ，实际的分数差异成比例增加。
  2. 恒定方差 (红线) : 标准差 (\(\sigma\)) 在概率范围内保持相对恒定。

这些实证发现验证了“线性高斯”假设，证实了快速闭式解不仅在数学上方便，而且基于现实。

处理偏差

成对比较的一个已知问题是位置偏差 。 LLM 往往偏爱首先出现的选项 (例如“答案 A”) ，仅仅因为它排在前面。

PoE 框架通过引入偏差项 \(\beta\) 优雅地处理了这个问题。如果模型是无偏差的，随机对的预期概率应该是 0.5。如果模型有偏差 (例如，它对第一个位置的平均概率为 0.6) ，我们可以通过移动高斯均值来进行补偿。

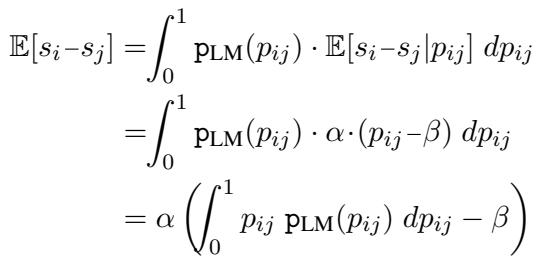
偏差修正公式。

通过将 \(\beta\) 设置为 LLM 在数据集上输出的平均概率，该框架有效地对分数进行了“去偏”，而无需运行两次比较 (A 对 B 以及 B 对 A) ，从而节省了 50% 的计算量。

智能比较选择

如果我们无法承担比较每一对文本的费用，我们应该比较哪些对？

由于高斯框架提供了分数不确定性 (协方差) 的闭式表达式，我们可以从数学上确定哪一次比较能最大限度地减少整体的不确定性。

目标是选择使信息矩阵的行列式最大化的对 \((i, j)\)。论文推导出了一个贪婪选择规则:

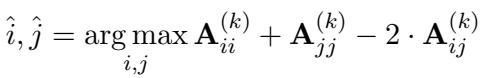
下一次比较的选择算法。

这里，\(\mathbf{A}\) 是逆协方差矩阵。这个公式允许系统主动选择信息量最大的比较——通常是当前估计分数不确定的对，或者被认为质量相近的项目。

实验结果

研究人员在几个标准的 NLG 数据集上评估了他们的框架，包括 SummEval (摘要) 和 TopicalChat (对话) 。他们将 PoE 方法与胜率 (Win-Ratio，简单计算获胜次数) 和标准 Bradley-Terry 等基准进行了比较。

效率提升

最关键的结果是该方法收敛到正确排名的速度有多快。

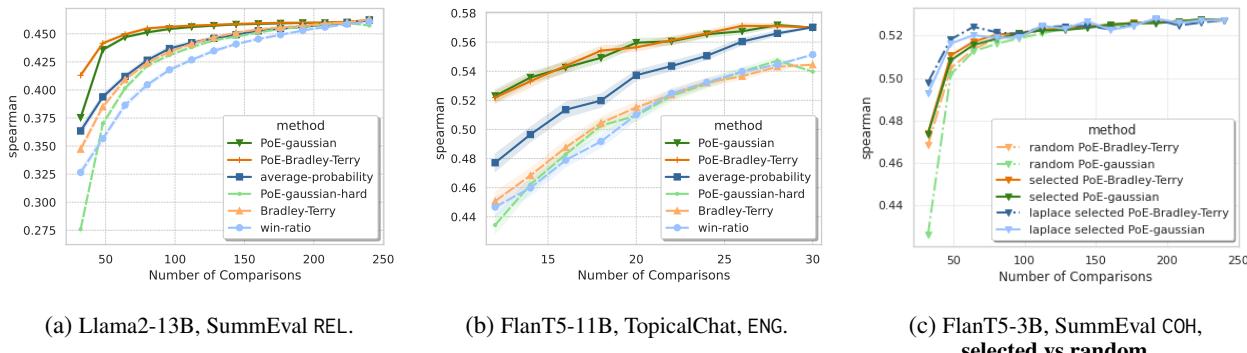
比较各种方法的效率曲线。

图 1 (上图) 说明了这一点:

  • 胜率 (Win-Ratio) (浅蓝色) 改进缓慢。它需要大量的比较才能获得不错的相关性。
  • PoE 方法 (高斯和 BT，绿色和红色线) 几乎立即飙升。仅使用一小部分比较 (低 \(K\) 值) ，它们就实现了与使用全集比较几乎相同的相关性。

例如，在 SummEval 上，仅使用 20% 的比较，PoE 方法就达到了 Win-Ratio 方法在使用 100% 比较后才达到的相关性分数。

大规模性能

该方法在大型数据集上表现得更加出色。在拥有超过 1,000 个候选者的 HANNA 数据集 (故事生成) 上，“全对”比较是不可能的 (超过 100 万次比较) 。

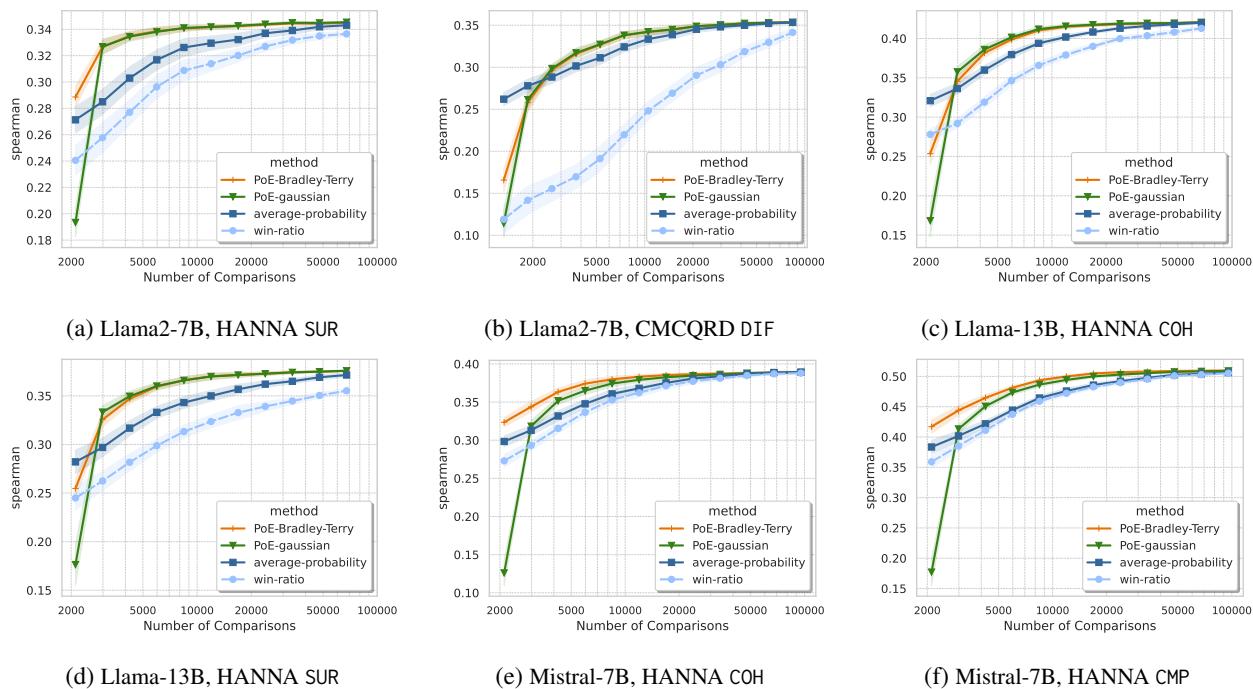
大规模数据集上的效率曲线。

如 图 6 所示，即使有成千上万的项目，PoE-Gaussian 方法 (绿色) 和 PoE-BT (橙色) 也比基准方法更快地收敛到高精度。它们提供了一种实用的方法来对大型排行榜进行排名，而不会让评估者破产。

性能总结

下表总结了 SummEval 上的 Spearman 相关性。请注意 PoE 方法 (最右侧几列) 如何始终优于胜率和平均概率，尤其是在 \(K\) (比较次数) 很小 (\(K=48\)) 的时候。

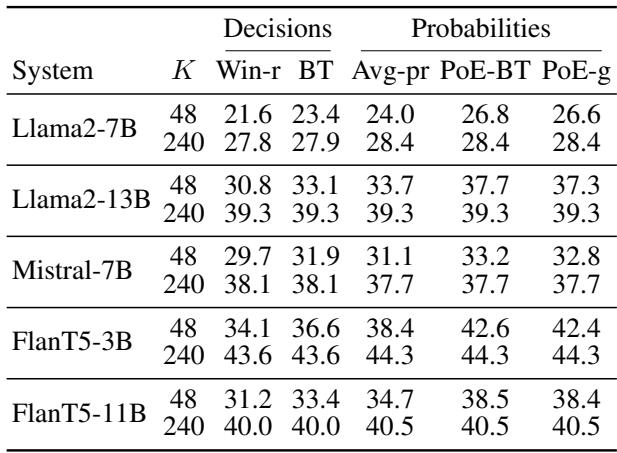
Spearman 相关性表。

结论

“LLM 作为裁判”的范式将继续存在，但比较每一对的暴力破解方法是不可持续的。这篇论文介绍了一个复杂但实用的解决方案。

通过将比较视为专家乘积 , 我们可以:

  1. 利用不确定性: 使用 LLM 的软概率，而不仅仅是二元决定。
  2. 快速计算: 使用高斯专家推导出只需要简单矩阵运算而不是迭代优化的闭式解。
  3. 节省资金: 仅使用总可能比较数的 2% 到 20% 即可获得高质量的排名。

该框架将成对评估从一项计算量巨大的任务转变为一个高效、有数学依据的过程。对于希望评估自己模型的学生和研究人员来说，这意味着你不需要巨额预算来获得精确的排名——你只需要正确的数学方法。

参考文献: Liusie, A., Fathullah, Y., Raina, V., & Gales, M. J. F. “Efficient LLM Comparative Assessment: A Product of Experts Framework for Pairwise Comparisons.” University of Cambridge.