引言

在自然语言处理 (NLP) 领域，判断两个句子是否表达相同的意思是一项基石般的任务。这种能力被称为语义文本相似度 (Semantic Textual Similarity, STS) ，它是搜索引擎、推荐系统、抄袭检测和聚类算法背后的核心动力。

多年来，业界一直在两大主要范式之间摇摆。一方是 Sentence-BERT , 一种可靠的架构，它独立地对句子进行编码；另一方是对比学习 (Contrastive Learning) (如 SimCSE) 的现代重量级模型，它们将最先进 (SOTA) 的性能推向了新高度。

然而，一个顽固的问题依然存在。对比学习模型通常以二元视角看待世界: 句子要么是“相似的” (正样本) ，要么是“不相似的” (负样本) 。但人类语言很少是非黑即白的。句子可能是“某种程度上相关”、“大体相似但在细节上不同”或“完全无关”。通过将这些细微差别强行塞入二元分类的桶中，或者将相似度分数视为独立的分类类别，我们丢失了宝贵的信息。

来自清华大学的研究人员最近发表了一篇题为 “Advancing Semantic Textual Similarity Modeling” 的论文，提出了一种视角的转变。他们不再将相似度视为分类问题，而是将其建模为回归问题 。 为了实现这一目标，他们提出了一种新颖的神经网络架构和两个在数学上具有创新性的损失函数: Translated ReLU 和 Smooth K2 Loss 。

在这篇文章中，我们将解构他们的方法，解释为什么将相似度视为一个连续的频谱——并为错误预留“缓冲区”——可以在使用更少计算资源的情况下超越传统方法。

---

背景: 当前的 STS 格局

要理解这篇论文的创新之处，我们需要先了解目前该领域主导的两种方法。

1. 孪生网络 (Sentence-BERT)

比较两个句子的标准方法是使用“孪生 (Siamese) ”网络结构 (双编码器) 。你将句子 A 输入 BERT 模型，将句子 B 输入同一个 BERT 模型 (共享参数) 。你为每个句子获得一个向量嵌入 (Embedding) 。然后比较这些向量以确定相似度。

Sentence-BERT 历史上将此视为一个分类任务。如果你有一个像 NLI (自然语言推理) 这样的数据集，其中包含“矛盾”、“中立”和“蕴含”等标签，模型会输出这三个离散类别的概率分布。

2. 对比学习 (SimCSE)

最近，对比学习占据了主导地位。这种方法在向量空间中拉近相似句子的嵌入，同时推开不相似句子的嵌入。虽然有效，但它有两个主要问题:

1. 二元限制: 它通常忽略细粒度的标签 (例如，5 分制中的 3 分) ，只关注极端情况 (0 对比 5) 。
2. 资源饥渴: 为了在训练中同时看到足够多的“负”样本，对比学习需要很大的批次大小 (Batch Size，通常 512+) 。这需要巨大的 GPU 显存。

研究人员认为，通过从根本上改变训练的目标，我们可以获得 Sentence-BERT 的效率以及对比学习的性能: 相似度应该是回归问题，而不是分类问题。

---

核心方法: 回归框架

这里的直觉很简单: 语义相似度是递进的。4 分比 1 分更接近 5 分。如果真值是“蕴含” (2 分) ，模型预测为“中立” (1 分) ，这个错误比预测为“矛盾” (0 分) 要小。

标准的分类损失函数 (如交叉熵) 将所有类别视为独立的；它们不理解“类别 2”比“类别 5”更接近“类别 3”。回归方法修正了这一点。

1. 架构

作者提出了一个改进的孪生网络。让我们看看架构图:

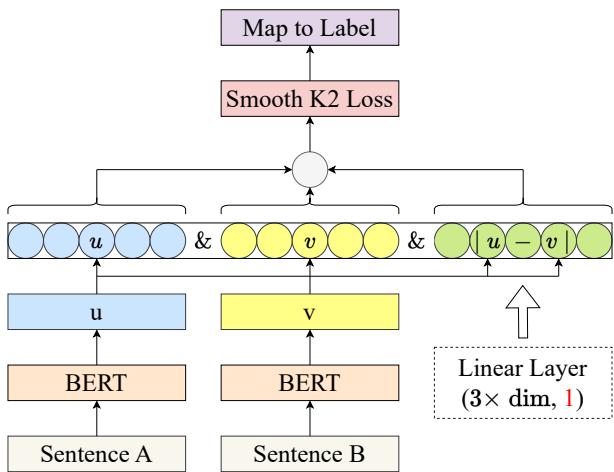
如图 Figure 1 所示，流程如下:

1. 输入: 两个句子，A 和 B。
2. 编码: 两者都通过预训练的 BERT 编码器，生成嵌入 \(u\) 和 \(v\)。
3. 特征工程: 模型拼接了三个元素:

• 向量 \(u\)
• 向量 \(v\)
• 逐元素差值 \(|u - v|\) (这捕捉了句子间的“距离”特征) 。

4. 回归头 (Regression Head) : 这个拼接后的向量通过一个全连接线性层。

• *关键变化: * 与输出 \(K\) 个节点 (每个类别一个) 的分类模型不同，该模型只有一个输出节点 。

这个单一节点输出一个代表相似度分数的连续浮点数。

2. “缓冲区” 概念

如果我们将其作为回归处理，为什么不直接使用标准的均方误差 (MSE) 或 L1 损失？

这里有一个微妙的洞察: 真实标签 (Ground Truth) 通常是离散点。 在 5 分制的相似度量表中，标签是 0, 1, 2, 3, 4, 5。 如果真实标签是 3，模型预测为 2.9 , 标准的回归损失会因为这 0.1 的差异而惩罚模型。

然而，如果我们将 2.9 四舍五入，得到的也是 3。分类是正确的！惩罚一个“足够接近”的模型会适得其反。它迫使模型纠结于精确的浮点数匹配，而不是学习通用的语义模式。

为了解决这个问题，作者引入了零梯度缓冲区 (Zero-Gradient Buffer Zone) 。 如果预测值与真实标签的距离在一定阈值内，损失即为零。这实际上是在告诉模型: “干得好，这就足够了。”

3. 损失函数 A: Translated ReLU

第一个提出的解决方案是 Translated ReLU (平移 ReLU) 。 它通过平移激活函数修改了标准的 L1 损失 (绝对差) 。

如果预测值与标签之间的距离小于阈值 \(x_0\)，则损失为 0。如果超过该阈值，损失线性增加。

\[ \begin{array} { l } { x \mathrm { a b s } ( \mathrm { p r e d i c t i o n - l a b e l } ) \geq 0 } \\ { f ( x ) = \{ \begin{array} { l l } { 0 \quad x < x _ { 0 } \leq \frac { d } { 2 } } \\ { k ( x - x _ { 0 } ) \quad x _ { 0 } \leq x } \end{array} } \\ { f ( x ) = \operatorname* { m a x } \bigl ( 0 , k ( x - x _ { 0 } ) \bigr ) } \end{array} \]

这里，\(d\) 代表类别之间的间隔 (例如，如果标签是 1, 2, 3，那么 \(d=1\)) 。只要误差小于间隔的一半 (\(d/2\)) ，四舍五入后的分类就是正确的。

4. 损失函数 B: Smooth K2 Loss

虽然 Translated ReLU 有效，但在损失开始产生的点上有一个尖锐的“拐角”。这种梯度的突变有时会导致训练不稳定。

为了使其平滑，作者提出了 Smooth K2 Loss (平滑 K2 损失) 。 这个函数同样有一个零损失的缓冲区，但当误差超过阈值 \(x_0\) 时，它呈二次方 (像曲线一样) 增长，而不是线性增长。

\[ \begin{array} { c } { { f ( x ) = \{ \displaystyle { 0 \quad x < x _ { 0 } \leq \frac { d } { 2 } } \quad x _ { 0 } \leq x } } \\ { { k ( x ^ { 2 } - 2 x _ { 0 } x + x _ { 0 } ^ { 2 } ) \quad x _ { 0 } \leq x } } \\ { { \frac { \partial f ( x ) } { \partial x } = \{ \displaystyle { 0 \quad x < x _ { 0 } \leq \frac { d } { 2 } } \qquad } } \\ { { 2 k ( x - x _ { 0 } ) \quad x _ { 0 } \leq x } } \end{array} \]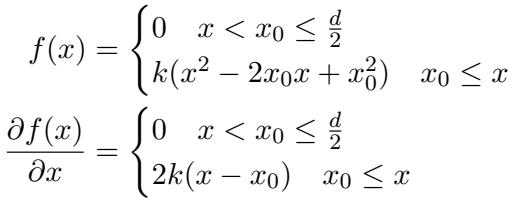

这种二次增长意味着，对于略微超出缓冲区的预测，模型的惩罚很轻；但对于远超出的预测，惩罚很重。这种动态梯度调整有助于模型优先处理最差的预测。

可视化差异

下图对比了两者。

• 左图: Translated ReLU。平坦，然后是一条向上的直线。
• 右图: Smooth K2 Loss。平坦，然后是一条向上的曲线。

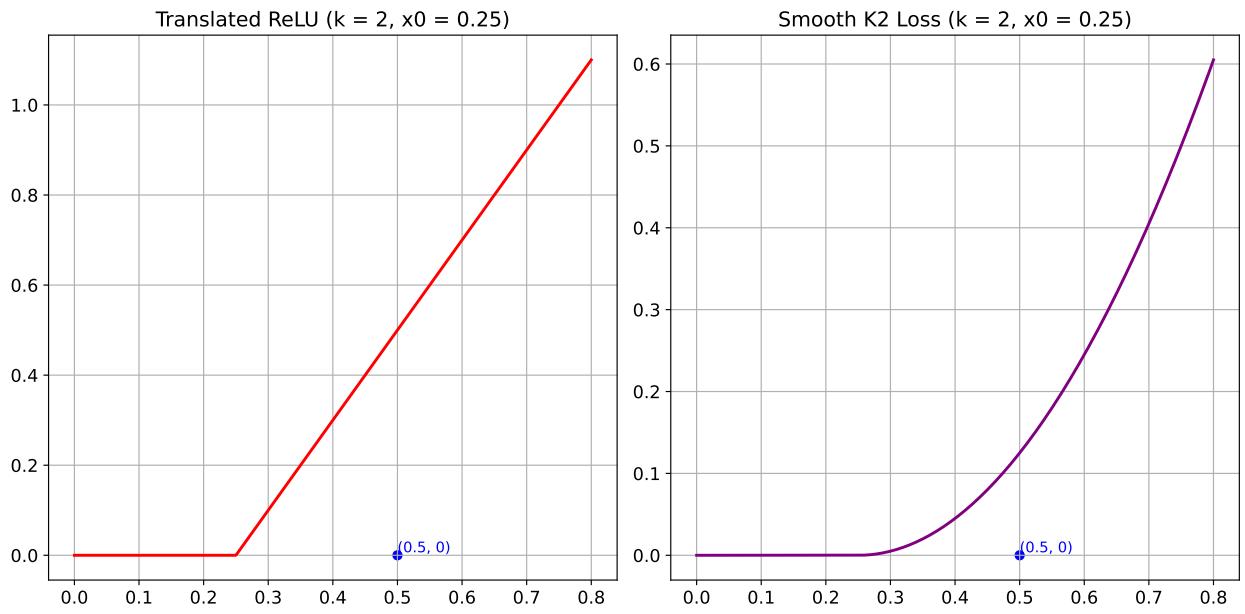
作者发现 Smooth K2 Loss 在高质量数据集上通常表现更好，因为它能提供可微分的、自适应的梯度。

---

实验与结果

研究人员在七个标准的 STS 基准 (STS 12-16, STS-B 和 SICK-R) 上测试了他们的框架。他们将自己的回归方法与传统的 Sentence-BERT 分类方法进行了比较。

1. 回归 vs. 分类

结果令人信服。在下表 (论文中的表 1) 中，我们可以看到 Spearman 相关系数得分 (越高越好) 。

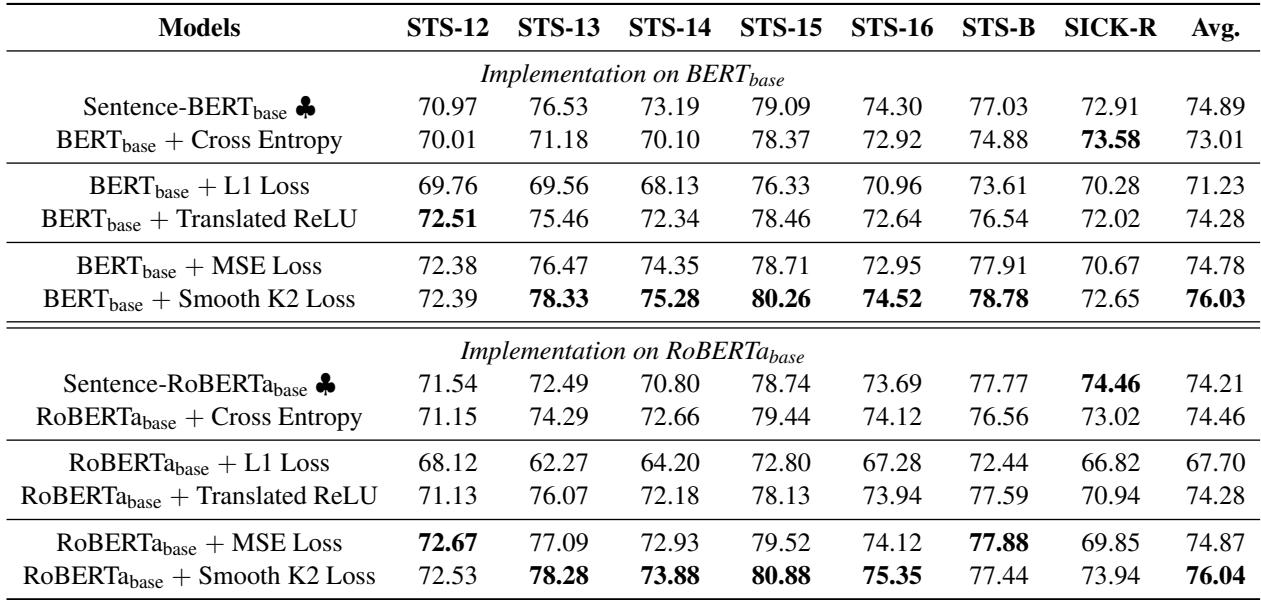
数据的主要结论:

• 回归获胜: 使用 Translated ReLU 或 Smooth K2 Loss 训练的模型始终优于标准的交叉熵 (分类) 方法。
• 缓冲区很关键: 新的损失函数优于标准的 L1 损失和 MSE 损失。这证明在 STS 任务中要求精确的浮点数匹配会损害性能。“缓冲区”允许模型更好地泛化。
• Smooth K2 占优: Smooth K2 Loss 取得了最高的平均得分 (在 BERT-base 上为 76.03) ，表明更平滑的梯度过渡确实有益。

2. 提升对比学习模型

论文中最令人兴奋的发现之一是，这个回归框架不仅可以替代旧模型，还可以增强最新、最强大的模型。

像 Jina Embeddings v2 和 Nomic Embed 这样的现代模型使用对比学习。研究人员使用他们的回归框架，配合特定的细粒度 STS 数据，对这些预训练的巨型模型进行了微调。

该过程包括一个两阶段的微调设置:

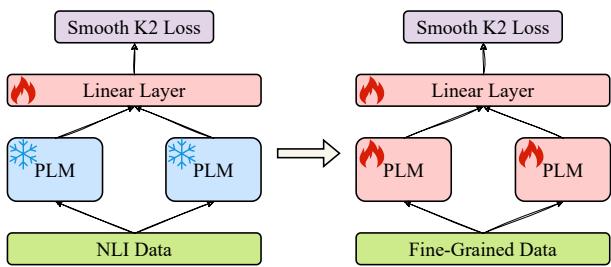
1. 阶段 1: 冻结预训练语言模型 (PLM) 。仅使用通用的 NLI 数据训练新的线性输出层。
2. 阶段 2: 解冻 PLM 并使用细粒度的 STS 数据 (配合 Smooth K2 Loss) 训练整个网络。

这种混合方法的结果如下所示:

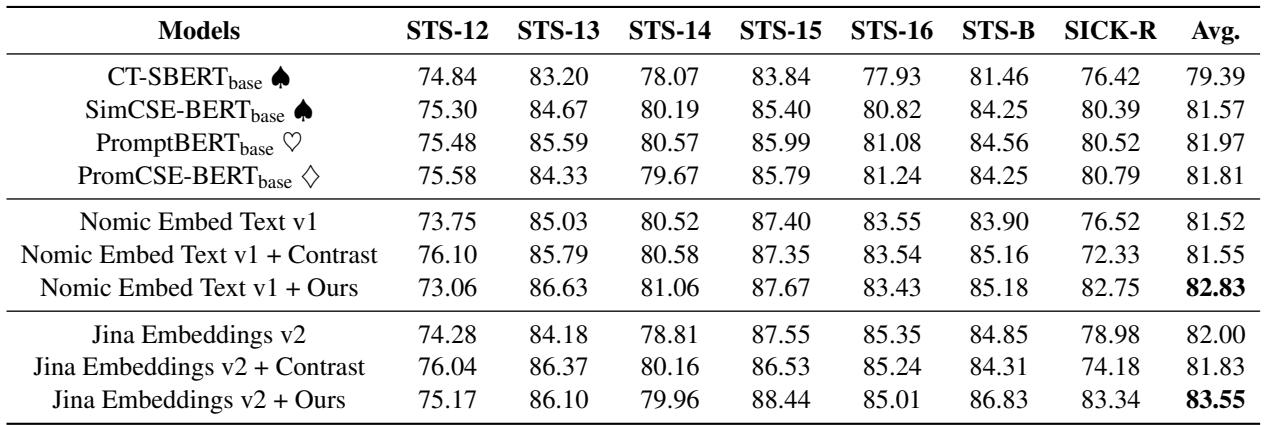
注意 “Jina Embeddings v2 + Ours” 和 “Nomic Embed Text v1 + Ours” 这两行。两者都显示出比基础模型明显的提升，甚至超过了进一步使用对比学习微调的模型 ("+ Contrast") 。这凸显了对比学习的一个主要局限性: 因为它依赖于二元的正/负样本对，它丢弃了“中等相关”句子的细微差别。回归框架捕捉到了这种细微差别。

3. 效率

最后，让我们谈谈计算成本。对比学习 (如 SimCSE) 需要巨大的批次大小来防止“模型坍塌” (即模型将所有东西都映射到同一个点) 。SimCSE 通常使用 512 的批次大小。

由于回归框架独立处理样本对 (或以小批次处理) ，它的效率极高。

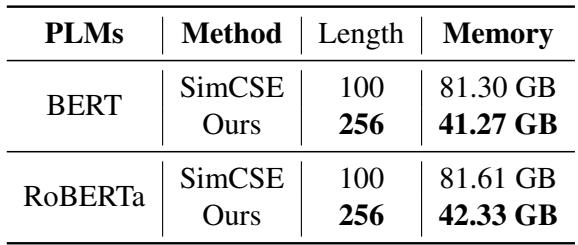
如 Table 4 所示，SimCSE 在序列长度为 100 时需要超过 81 GB 的显存来训练。提出的回归方法仅使用一半的显存( 41 GB )，同时支持 256 的序列长度 (长 2.5 倍！) 。这使得拥有消费级硬件的研究人员也能进行高性能的 STS 建模。

---

结论

“Advancing Semantic Textual Similarity Modeling” 这篇研究论文从庞大的对比学习设置的复杂性中走出来，提供了一个令人耳目一新的视角。通过识别出语义相似度本质上是一个递进的、连续的概念 , 作者成功地论证了回归驱动的孪生架构的回归。

核心创新——Translated ReLU 和 Smooth K2 Loss——提供了所需的数学灵活性，将离散标签视为连续目标。通过结合零梯度缓冲区，这些损失函数防止了模型对精确数值的过拟合，使其能够专注于理解语义距离。

对于学生和从业者来说，启示很明确:

1. 不要忽视标签的本质。 如果你的类别有顺序 (好、更好、最好) ，分类损失可能是次优的。
2. 损失函数可以有创造性。 修改标准损失以包含边界或缓冲区可以显着影响性能。
3. 效率很重要。 这个回归框架在不需要工业级 GPU 集群的情况下实现了最先进的结果。

这项工作为更智能、更精简和更细致的文本理解模型铺平了道路，弥合了僵化的分类与资源密集型对比学习之间的鸿沟。

---