引言

在大型语言模型 (LLM) 飞速发展的格局中，似乎每周都会诞生一种新的“推理策略”。我们早已超越了简单的提示工程 (Prompting) 。现在，我们拥有了能够相互辩论的智能体、构建“思维树”的算法，以及能够反思自身错误并进行自我修正的系统。

介绍这些方法的论文通常会展示令人印象深刻的图表，显示其新颖、复杂的策略在排行榜上独占鳌头，将简单的提示技术远远甩在身后。但这其中存在一个陷阱——或者说一个在学术比较中经常被忽视的隐藏变量: 计算预算 (Compute Budget) 。

想象一下比较两个学生在数学考试中的表现。学生 A 必须立即回答。学生 B 则被允许写十份草稿，咨询三个朋友，并且多花一个小时的时间。如果学生 B 的分数略高，是因为他们更聪明，还是仅仅因为他们拥有更多的资源？

这就是研究论文 “Reasoning in Token Economies: Budget-Aware Evaluation of LLM Reasoning Strategies” (Token 经济中的推理: LLM 推理策略的预算感知评估) 背后的核心问题。作者认为，传统的评估是“规模无关 (scale-agnostic) ”的，这意味着它们忽略了推理的成本。当我们对“Token 预算”——即生成答案的实际计算成本——进行归一化处理时，LLM 推理的格局发生了巨大的变化。

在这篇文章中，我们将解构这篇论文，以理解为什么像 结合自洽性的思维链 (Chain-of-Thought with Self-Consistency) 这样简单的方法可能实际上是我们拥有的最高效的“聪明”策略，以及为什么复杂的多智能体系统往往难以证明其高昂成本的合理性。

背景: 推理策略大观园

在深入探讨预算之争之前，我们需要了解参赛选手。提示工程领域已经演变为“推理时推理策略 (Inference-Time Reasoning Strategies) ”。以下是本次分析中讨论的主要参与者:

1. 思维链 (CoT) 与自洽性 (SC)

最著名的高级提示技术是 思维链 (Chain-of-Thought, CoT) 。 与其直接询问答案，不如要求模型“一步步思考”。 自洽性 (Self-Consistency, SC) 则更进一步。你将 CoT 提示运行多次 (采样) 以生成不同的推理路径和答案。然后，进行多数投票。如果 10 条路径中有 7 条得出的答案是“42”，模型就会输出“42”。

2. 复杂策略

研究人员试图设计更像人类的推理过程:

  • 多智能体辩论 (Multi-Agent Debate, MAD): 多个 LLM 实例 (“智能体”) 提出答案，互相批评，并经过多轮迭代以达成共识。
  • 反思 (Reflexion): 模型生成答案，批评自己的输出以查找错误，然后基于该反馈再次尝试。
  • 思维树 (Tree of Thoughts, ToT): 模型探索可能性的搜索树。它生成多个下一步，对其进行评估，并仅保留有希望的分支，类似于国际象棋引擎的预判。

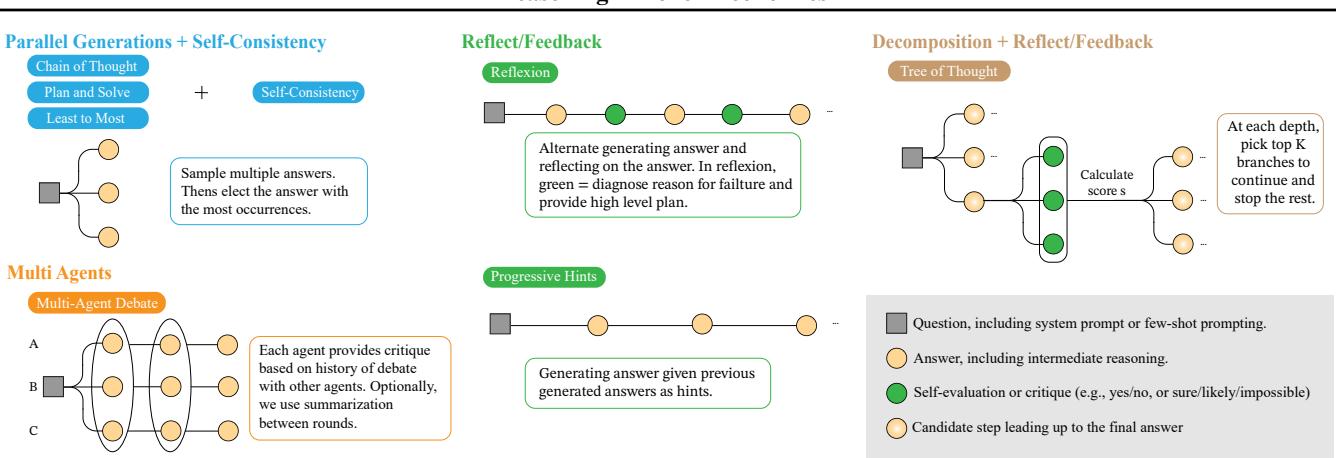
推理策略概览。绿色单元格表示问题提示词，橙色表示答案，蓝色表示评估。

如 图 2 所示，这些策略在复杂性上差异巨大。CoT 是线性的。Reflexion 涉及循环。思维树涉及分支。自然地，图表右侧的方法比单个提示消耗的 Token 和 API 调用要多得多。

核心问题: “规模无关”的错觉

该论文的核心论点是，不看成本地比较这些策略是不公平的。

在“规模无关”的评估 (标准方法) 中，研究人员可能会比较 单智能体 CoT 和 多智能体辩论 (3 轮，6 个智能体) 。

  • 单智能体可能生成 500 个 Token。
  • 多智能体辩论随着智能体之间的来回对话，可能生成 10,000 个 Token。

如果辩论策略以 2% 的优势胜出，它就被宣布为更优的方法。但是，如果我们允许单智能体 CoT 采样 20 次 (自洽性) ，使其也使用 10,000 个 Token 呢？那时谁会赢？

定义预算

作者提出了一个 预算感知评估框架 (Budget-Aware Evaluation Framework) 。 他们通过两种方式衡量预算:

  1. 查询次数 (Number of Queries): 我们调用 API 多少次？ (对延迟和速率限制很重要) 。
  2. Token 数量 (Number of Tokens): 输入和输出 Token 的总和。 (对经济成本和计算负载很重要) 。

当我们透过这个镜头观察排行榜时，排名发生了翻转。

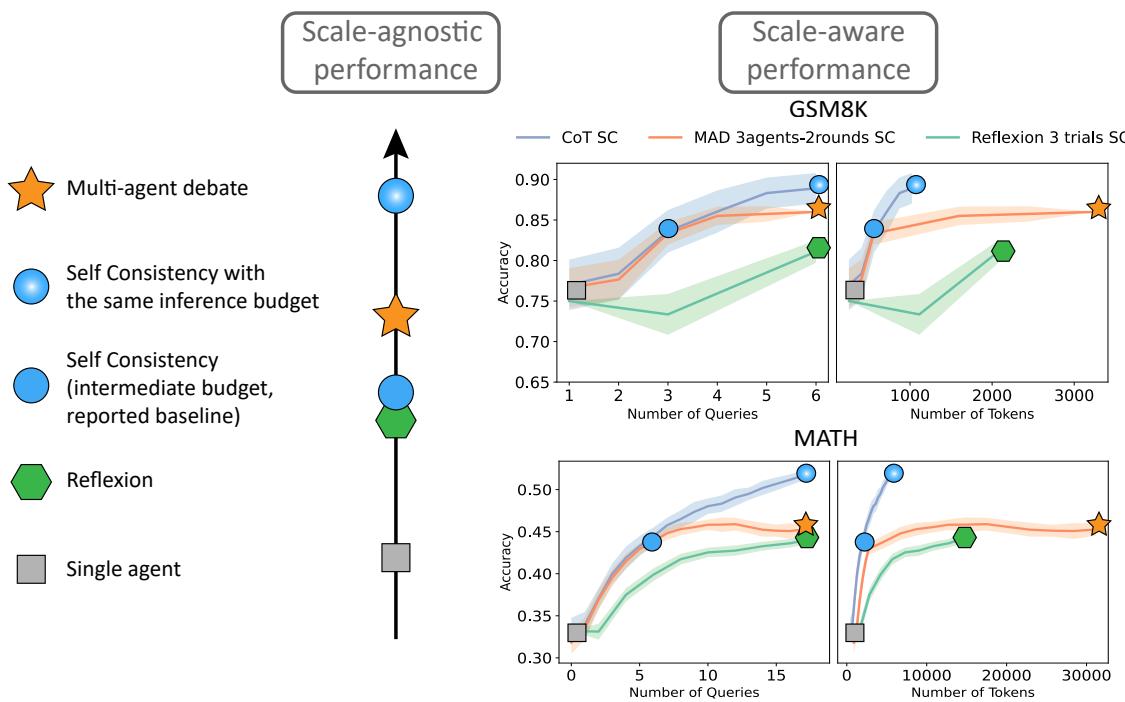
推理方法的比较: 规模无关与规模感知性能对比。

上方的 图 1 完美地展示了这一现象。

  • 左侧 (规模无关) : 多智能体辩论 (橙色星号) 似乎在碾压单智能体 (灰色方块) 。
  • 右侧 (规模感知) : 当我们将性能与 Token 数量 (x 轴) 绘制在一起时，多智能体曲线 (橙色) 和 Reflexion 曲线 (绿色) 通常位于简单的 CoT 自洽性曲线 (蓝色) 下方 。

这揭示了复杂智能体的所谓“算法上的精妙设计”，实际上可能只是使用了更多算力的暴力破解结果。

核心方法: 探究权衡

研究人员在五个截然不同的数据集上进行了广泛的评估，范围从数学问题 (GSM8K, MATH) 到常识推理 (CSQA) 和多跳问答 (HotpotQA) 。他们测试了 GPT-3.5、GPT-4 以及像 Llama-2 和 Mistral 这样的开源模型。

他们的方法论非常严谨: 严格的预算匹配。如果像“计划与求解 (Plan-and-Solve) ”这样的复杂策略使用 5,000 个 Token 来回答一个问题，那么基线 (CoT SC) 也被允许进行足够多次的采样，以同样消耗 5,000 个 Token。

结果: 简单策略的反击

结果是一致的，且有些出人意料。在几乎所有数据集上, 结合自洽性的思维链 (CoT SC) 被证明是最高效的策略。

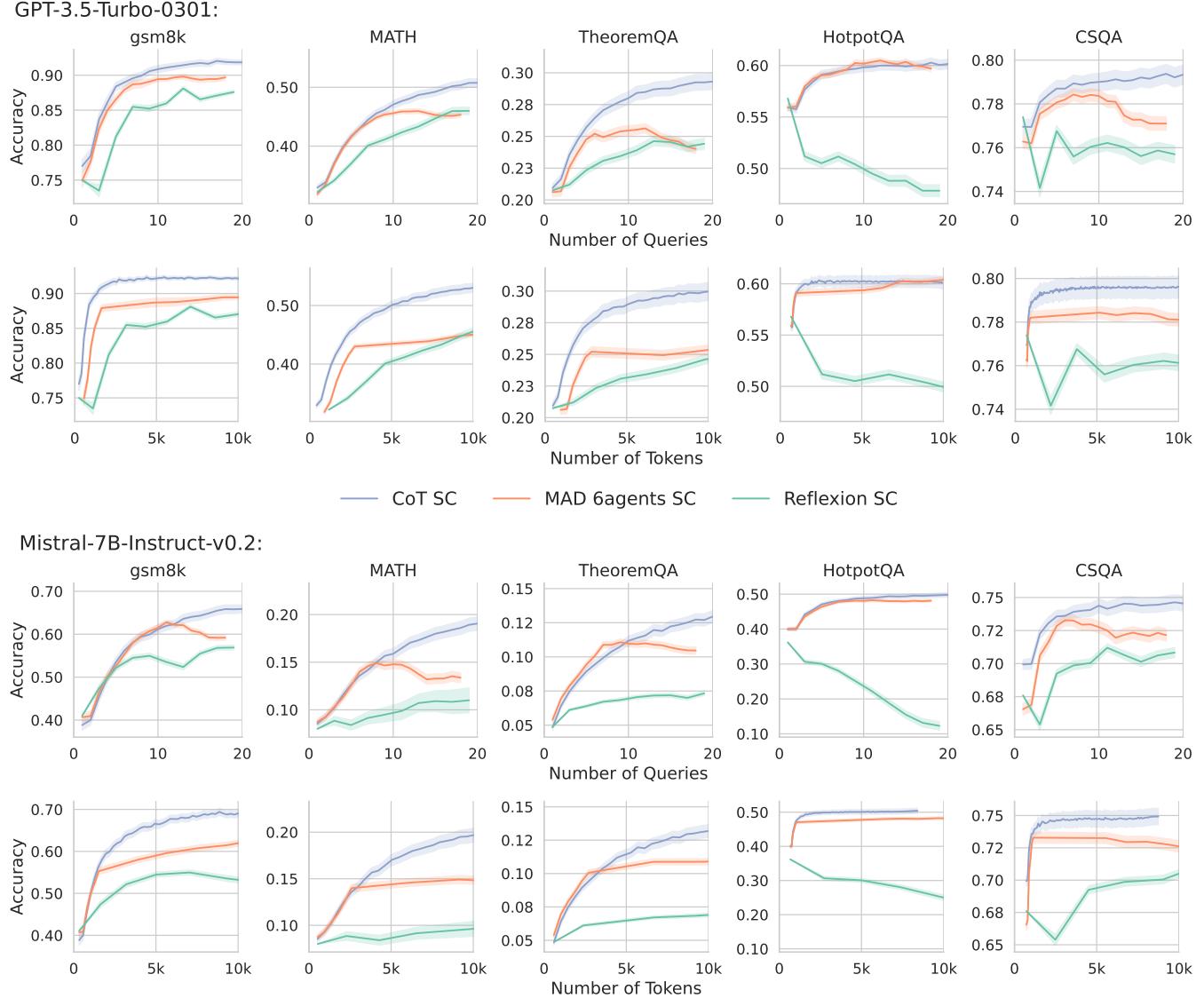
CoT SC、MAD 和 Reflexion 在 5 个数据集上的性能图表。

请看上面的 图 3 。

  • 蓝线 (CoT SC): 随着预算 (查询/Token) 的增加，准确率稳步攀升。
  • 橙线 (MAD): 在许多情况下，特别是在数学数据集中，它开始时具有竞争力，但最终会进入平台期，甚至表现不如蓝线。
  • 绿线 (Reflexion): 它通常明显落后。

结论是什么？如果你每个问题的预算是 3,000 个 Token，通常情况下，对一个简单的 CoT 提示采样 15 次并进行多数投票，比运行复杂的 3 轮智能体辩论要好得多。

为什么复杂策略会失利？

直觉上，“辩论”或“反思”应该能产生更好的答案。为什么简单的投票会击败它们？作者研究了这背后的理论机制。

1. 辩论中的多样性问题

在多智能体辩论 (MAD) 中，智能体可以看到彼此的回答。这产生了依赖性。如果智能体 A 自信地产生了一个错误的幻觉答案，智能体 B 可能会被动摇而附和。随着辩论轮次的继续，池中的“多样性”会减少。它们都会收敛，但可能会收敛到 错误 的答案上。

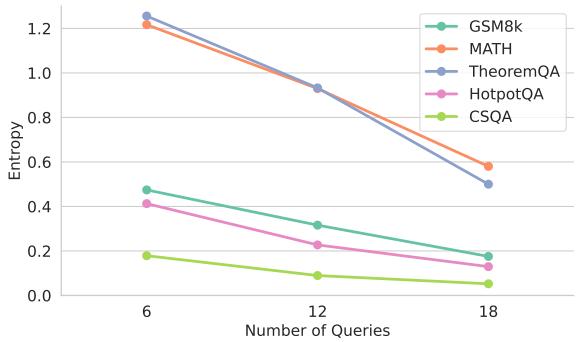
MAD 中答案的多样性度量 (熵) 随轮次下降。

图 6 显示，随着辩论轮次的推进 (从查询 6 到 18) ，答案的熵 (多样性的一种度量) 急剧下降。相比之下，自洽性保持每个样本独立。独立性对于“群体智慧”效应至关重要——只有当错误不相关时，它们才会相互抵消。

2. 自洽性背后的数学原理

作者提供了一个数学框架来解释为什么自洽性 (SC) 的扩展性如此之好。他们使用二项分布和狄利克雷分布来对正确多数投票的概率进行建模。

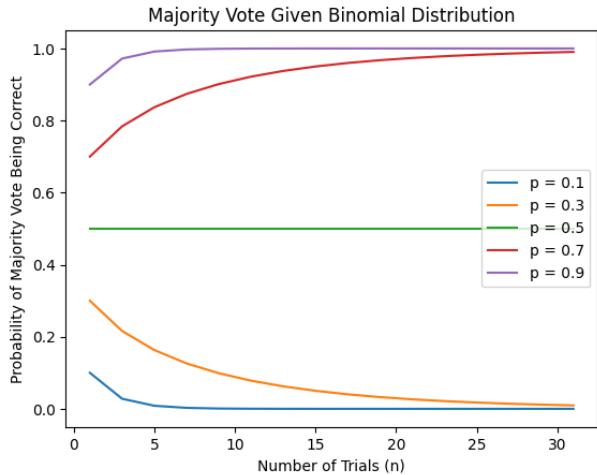
不同 Beta 分布下自洽性的收敛情况。

如 图 12 (上图的一部分) 所示，如果模型在单次尝试中正确的概率大于 50% (\(p > 0.5\))，随着样本量 (\(N\)) 的增加，多数投票正确的概率 (\(P(\text{MV correct})\)) 会收敛到 100%。

本质上，SC 纯粹通过独立采样的统计学原理，将一个“不错”的模型变成了一个“卓越”的模型。复杂的策略引入了破坏这种数学保证的依赖性。

“树”与“评估者”

该论文还特别关注了 思维树 (ToT) 以及对于像 Reflexion 这类策略至关重要的 自我评估 (Self-Evaluation) 概念。

思维树: 昂贵但有效？

思维树 (ToT) 是少数几个在基线面前显示出潜力的策略之一，特别是在像“24点游戏” (一种数学谜题) 这样的困难任务上。然而，ToT 需要两个组件:

  1. 提议者 (Proposer): 生成后续步骤。
  2. 评估者 (Evaluator): 对这些步骤进行评分。

作者发现 ToT 极其昂贵。此外，它严重依赖于模型的能力。

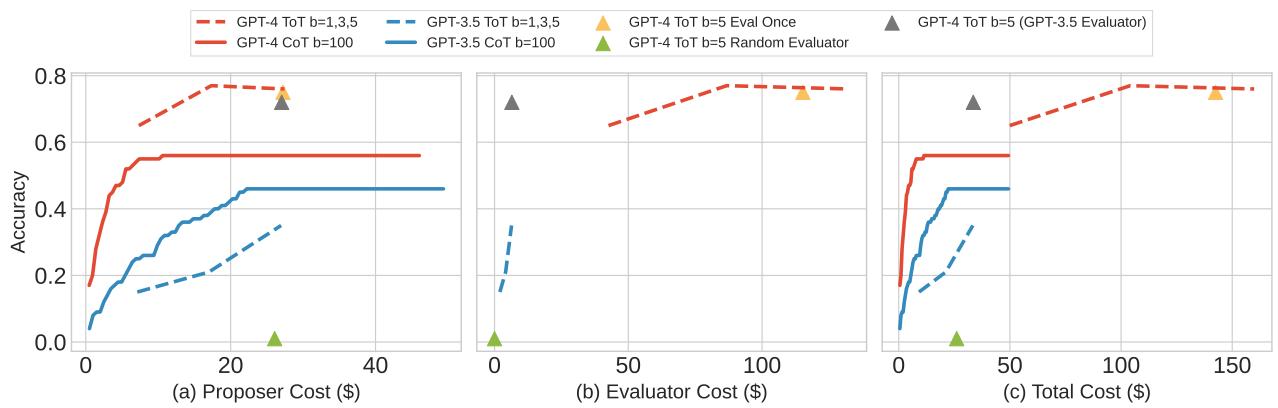
24点游戏中 ToT 与 CoT 的准确率与成本对比。

在 图 8 中，我们可以看到成本 (美元) 与准确率的关系。ToT (虚线/点线) 确实可以达到比 CoT (实线) 更高的准确率，但请看 X 轴上的成本。为了获得这种提升，你可能需要为每个问题支付 10 倍或 20 倍的费用。对于许多应用来说，这种边际收益递减是不可行的。

自我评估的弱点

像 Reflexion 和 ToT 这样的策略依赖于 LLM 检查自己工作并说“这是错的”的能力。

研究人员测试了这种“自我评估”能力，发现它并不尽如人意。他们比较了让模型自我评估的不同方式 (是/否，1-10 评分，概率) 。

数学推理数据集的校准结果。

图 15 (上图顶部) 揭示了一个校准问题。理想情况下，如果模型有 80% 的自信 (x 轴) ，它应该有 80% 的正确率 (y 轴) 。曲线显示出显著的偏差。

  • 表 2 强调，在 MATH 数据集上，“错误准确率 (Incorrect Accuracy) ”很低。这意味着当模型出错时，它通常意识不到。

如果 LLM 无法准确检测出自己的错误，像 Reflexion 这样的策略就会变得“盲目”——它们在答案上迭代，但不一定能改进它。

新希望: 自度信自洽性 (\(SC^2\))

尽管校准效果不佳，作者还是找到了一种从自我评估中挖掘价值的方法。他们提出了 \(SC^2\) (Self-Confident Self-Consistency，自度信自洽性) 。

他们不再使用简单的多数投票 (1 人 = 1 票) ，而是根据模型对该答案的置信度对投票进行加权。即使校准不完美，它也提供了足够的信号来过滤掉置信度非常低的幻觉。

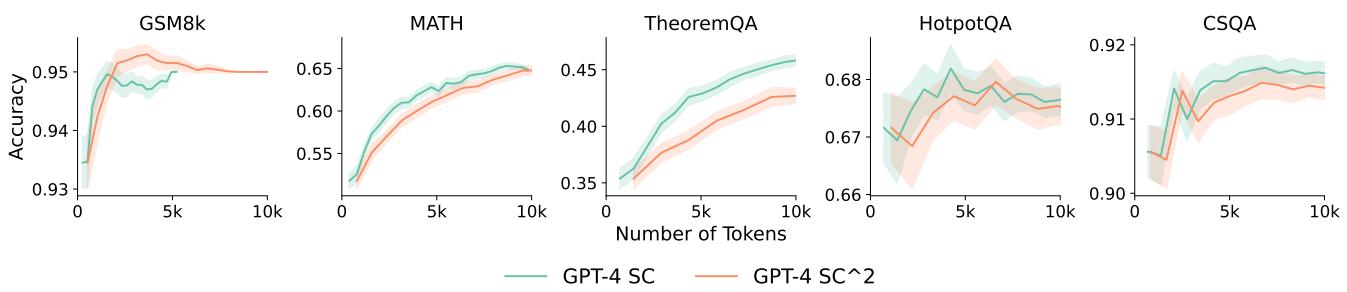
SC^2 与 SC 在数学推理任务上的性能对比。

正如 图 16 所示，\(SC^2\) (橙线) 在数学数据集 (GSM8K, MATH) 上的表现优于标准 SC (绿线) 。这表明，虽然复杂的反思循环可能会失败，但简单地问模型“你确定吗？”并利用它来加权投票，是一种预算高效的改进方法。

结论: 对 AI 开发的启示

这篇论文是对 AI 社区的一次现实检验。它将焦点从“新颖的架构”转回到概率和计算效率的基本面上。

给学生和从业者的关键启示:

  1. 计算 Token: 永远不要仅凭准确率来判断推理策略。永远要问: “成本是多少？”
  2. 基线难以逾越: 简单的结合自洽性的思维链 (CoT SC) 是一个非常稳健的基线。如果一篇新论文声称击败了它，请检查他们是否匹配了计算预算。
  3. 独立性很重要: 在设计多智能体系统时，要警惕“群体迷思”。独立采样 (SC) 通常能击败协作辩论，因为错误保持不相关。
  4. 自我纠错很难: 不要假设 LLM 能够修复自己的错误。目前的模型往往过度自信，且不善于自我诊断。

随着我们向前发展，“Token 经济”将主导部署。理论上的改进令人兴奋，但在现实世界中，每美元 (或每 GPU 秒) 能提供最佳答案的策略将会胜出。目前，这个赢家往往是那种简单、符合统计学原理的方法: 要求模型“一步步思考”，然后进行多数投票。

方程对比

对于对数学感兴趣的读者，论文将自洽性的成功归因于二项分布的收敛。

单个样本正确的概率被建模为伯努利试验。多数投票 (MV) 正确的概率是获得至少 \(n/2\) 个正确投票的概率之和:

\[ P ( { \mathrm { M V ~ c o r r e c t } } | x _ { i } ) = \sum _ { k = \lceil n / 2 \rceil } ^ { n } { \binom { n } { k } } p _ { i } ^ { k } ( 1 - p _ { i } ) ^ { n - k } . \]

随着 \(n\) (预算) 趋向于无穷大，该函数表现为一个 S 形曲线 (Sigmoid) ，只要基础准确率 \(p_i\) 高于 0.5，它就会将准确率推向 100%:

\[ \operatorname* { l i m } _ { n \infty } P ( \mathrm { M V } \mathrm { c o r r e c t } | x _ { i } ) = \{ { 1 \atop 0 } \mathrm { ~ i f ~ } p _ { i } > 0 . 5 , \]

这种数学上的必然性解释了为什么与复杂的、依赖性的链式 (错误可能会复合) 相比，将算力投入到独立采样 (SC) 中是如此有效。