引言: 遭遇 NLP 的瓶颈

如果你一直关注自然语言处理 (NLP) 的进展，特别是在句向量 (Sentence Embeddings) 领域，你可能已经注意到了一个趋势。我们已经从简单的词向量 (如 GloVe) 发展到复杂的基于 Transformer 的模型 (如 BERT) ，再到现在的大型语言模型 (LLM，如 LLaMA 和 Mistral) 。

句向量是现代 AI 应用的骨干。它们将文本转换为数值向量，使计算机能够理解“The cat sits on the mat” (猫坐在垫子上) 与“A feline is resting on the rug” (一只猫科动物在小地毯上休息) 在语义上是相似的。这项技术支撑着从 Google 搜索到检索增强生成 (RAG) 系统的方方面面。

衡量这些向量质量的标准方法是语义文本相似度 (STS) 。 我们使用基准测试 (如 SentEval 工具包) 来查看模型的相似度评分与人类判断的相关性如何。

多年来，分数一直在上升。但最近，我们遇到了一堵墙。

看看目前的最新水平 (SOTA) :

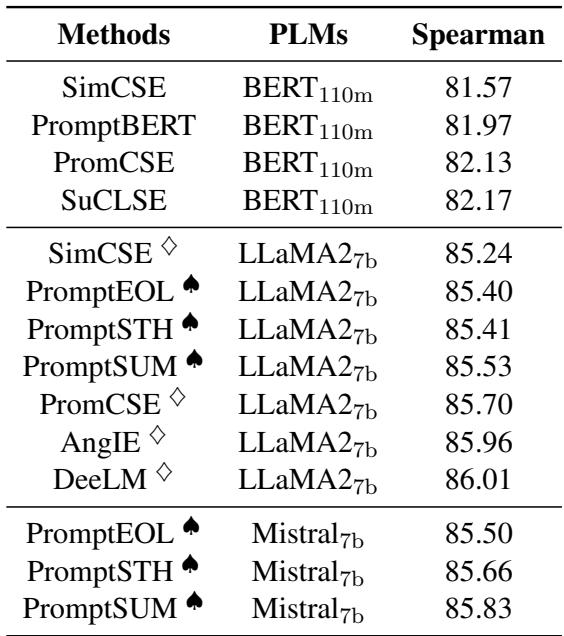
无论研究人员使用的是 BERT (1.1 亿参数) 还是巨大的 LLaMA 模型 (70 亿参数) ，也不管他们采用了何种提示工程或对比学习技巧，平均斯皮尔曼相关系数得分似乎都卡在了 86.5 左右。

86.5 仅仅是 LLM 理解能力的极限吗？还是我们的训练方式存在根本性的缺陷？

在这篇文章中，我们将深入探讨一篇引人入胜的论文: “PCC-tuning: Breaking the Contrastive Learning Ceiling in Semantic Textual Similarity” (PCC-tuning: 打破语义文本相似度中的对比学习天花板) 。 这项研究不仅提出了一个新的模型，还从数学上证明了我们要目前最喜欢的训练方法——对比学习——存在 87.5 的理论性能上限。

更重要的是，作者提出了一种解决方案——Pcc-tuning , 通过改变游戏规则来突破这一天花板。

背景: 对比学习时代

要理解我们为何触碰到天花板，首先需要了解我们是如何一步步走到这里的。当今句子表示的主流范式是对比学习 (Contrastive Learning) 。

对比学习的直觉简单而优雅:

1. 取一个句子 (锚点 Anchor) 。
2. 创建一个它的“正样本”版本 (例如，通过使用 Dropout 噪声或同义改写) 。
3. 将批次 (Batch) 中的其他句子视为“负样本”。
4. 训练模型在向量空间中拉近锚点与正样本的距离，同时推开负样本。

为此最流行的损失函数是 InfoNCE Loss 。

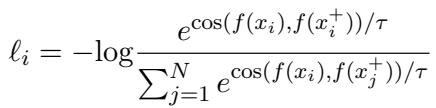
在这个公式中:

• 分子计算样本 \(x_i\) 与其正样本对 \(x_i^+\) 之间的相似度。
• 分母将 \(x_i\) 与所有其他样本 (负样本) 之间的相似度求和。
• 通过最小化这个损失，我们将正样本对相对于负样本的相似度最大化。

这种方法由 SimCSE 等模型推广，彻底改变了该领域。它使模型无需为每一对句子都提供昂贵的人工标注数据，就能学习到鲁棒的语义空间。

然而，今天的论文作者认为，这种优势也正是其最大的弱点。

理论天花板: 为什么是 87.5？

这是研究中最具突破性的部分。作者提出了一个关键问题: 对比学习实际上是如何看待语义相似度的?

对比学习即二分类器

当我们使用 InfoNCE 损失时，我们本质上是在告诉模型执行一个二分类任务:

• 类别 1 (正类) : 这对句子是相似的。
• 类别 0 (负类) : 这对句子是不相似的。

模型被训练来区分“自己人” (正样本) 和“其他人” (负样本) 。它并没有被明确训练去说“句子 A 与句子 B 有 80% 相似，但与句子 C 只有 40% 相似”。它建立的是一种粗粒度的区分。

理想情况下，一个完美的对比学习模型就像一个最优二分类器 。

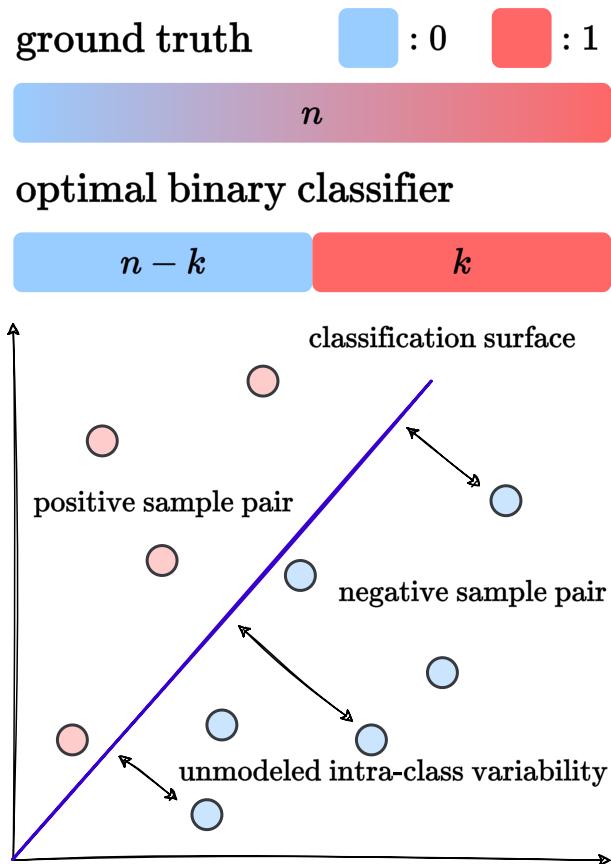
如上图所示，一个完美的二分类器将数据分成两块。它给前 \(k\) 个最相似的对分配高相似度分数 (比如 1) ，给其余 \(n-k\) 个对分配低分数 (比如 0) 。

问题在哪? 人类的语义相似度不是二元的。 它是一个连续的谱系。通过强迫模型学习二元区分，我们限制了它精确排序句子的能力。

推导极限

为了证明这一限制，作者研究了用于评估这些模型的指标: 斯皮尔曼相关系数 (Spearman’s Correlation Coefficient, \(\rho\)) 。

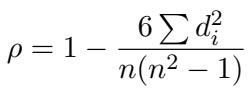
斯皮尔曼相关系数衡量的是排名顺序 (Rank Order) 。 它不关心原始数值，只关心如果人类将 A 对排在 B 对之前，模型是否也这样做。变量 \(d_i\) 代表第 \(i\) 个项目在人类排名和模型排名之间的差异。

如果我们的对比学习模型充当一个最优二分类器，它实际上将数据分成了两组。在“正样本”组内，模型认为所有对的相似度都是相等的 (排名并列) 。在“负样本”组内，它也认为所有对都是同等不相似的。

作者对这种二元情况下的排名差异 (\(d_i\)) 进行了数学建模:

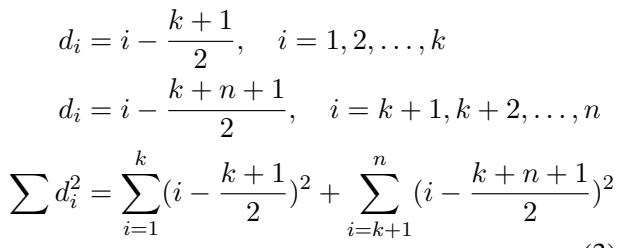
在这里，模型将前 \(k\) 个项目分类为正样本，其余分类为负样本。即使在这个“完美”的二元场景中，模型也会产生排名误差，因为它无法区分正样本组内部或负样本组内部的差异。

通过展开排名差平方和 (\(\sum d_i^2\)) ，他们推导出了一个依赖于 \(n\) (总样本数) 和 \(k\) (正样本阈值) 的函数:

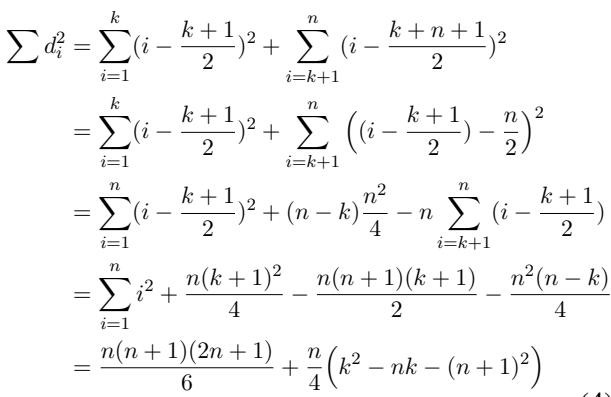
为了找到最佳可能的性能，我们需要最小化这个误差。事实证明，当 \(k = n/2\) 时——即二分类器将正好一半的数据视为正样本，一半视为负样本时——误差最小。

将这个最佳状态代回斯皮尔曼公式:

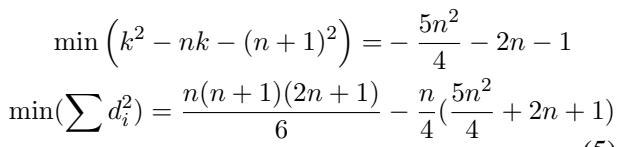
最后，取数据集大小 \(n\) 趋于无穷大的极限，我们得出了理论上限:

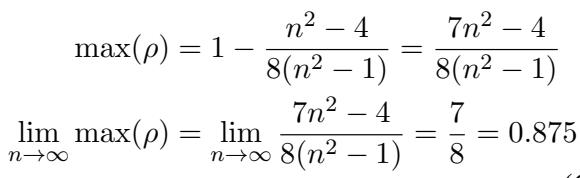
结果是 0.875。

这个推导意义深远。它表明，只要我们仅依赖标准的对比学习 (其行为类似于二分类器) ，我们在数学上就无法获得高于 87.5 的斯皮尔曼相关系数。表 1 中观察到的约 86.5 的平台期并非模型的失败；这是损失函数的固有属性。

解决方案: Pcc-tuning

要打破损失函数强加的天花板，我们必须改变损失函数。作者提出了 Pcc-tuning (皮尔逊相关系数微调) 。

其核心思想是停止将相似度视为二分类问题 (相似 vs 不相似) ，而是开始将其视为尊重语义关系连续性的回归问题。

两阶段架构

Pcc-tuning 采用两阶段的训练流程。

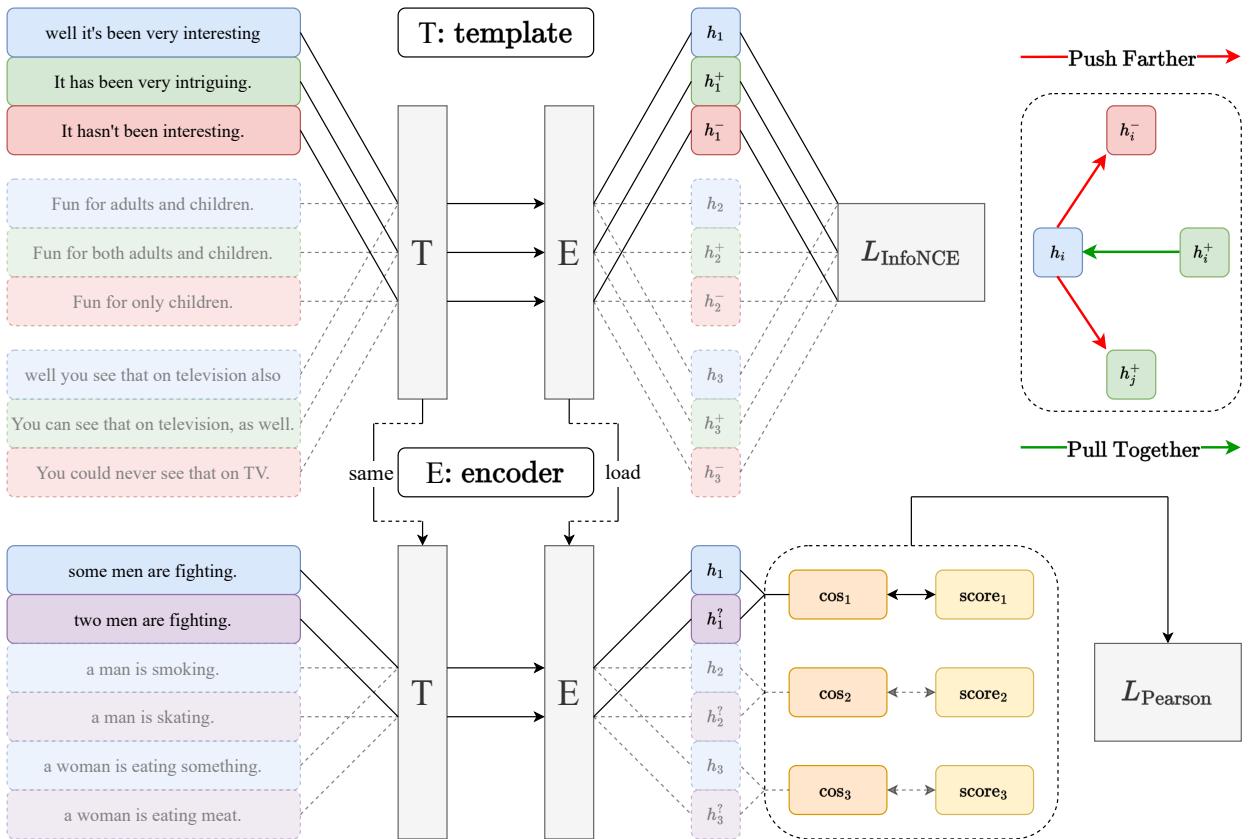
第一阶段: 对比预训练 (热身)

我们不能简单地抛弃对比学习。它在创建均匀的语义空间和修复 PLM 中常见的“各向异性”问题 (即嵌入塌缩成一个狭窄的锥体) 方面非常有效。

• 方法: 使用标准的 InfoNCE 损失在大型自然语言推理 (NLI) 数据集上对模型进行微调。
• 结果: 这给了我们一个强大的“基础”模型，它理解一般的语义关系，但仍受限于二元天花板。

第二阶段: Pcc-tuning (精炼)

这是见证奇迹的时刻。

• 数据: 少量细粒度标注数据 (具体来说，是经过过滤的 STS-B 和 SICK-R 训练集) 。我们谈论的是大约 5,000 个文本对，与第一阶段使用的数十万数据相比微不足道。
• 损失函数: 模型不再使用 InfoNCE，而是最小化负皮尔逊相关系数 (Pearson Correlation Coefficient) 。

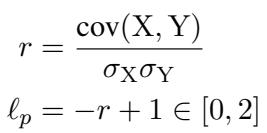
在这个公式中:

• \(X\) 代表模型预测的余弦相似度。
• \(Y\) 代表连续的人工标注分数 (例如 4.2/5.0) 。
• \(r\) 是它们之间的皮尔逊相关系数。
• 损失为 \(\ell_p = -r + 1\)。最小化该损失即最大化相关性。

通过直接针对相关性进行优化，模型学习到了对比学习所忽略的细粒度细微差别。它学会了得分为 4.5 的对应该比得分为 3.0 的对更接近，而不是简单地将它们都归为“正样本”。

实验与结果

理论在实践中站得住脚吗？作者在几个 70 亿参数模型 (OPT, LLaMA, LLaMA2, Mistral) 上测试了 Pcc-tuning。

打破天花板

结果显示，Pcc-tuning 始终超越了之前的最新技术水平 (SOTA) 。

虽然之前的方法如 PromptEOL 和 DeeLM 徘徊在 85-86 之间，但 Pcc-tuning 在 Mistral-7b 上取得了 87.86 的分数。这有效地打破了对比学习方法 87.5 的理论天花板。

质量 vs. 数量: Pcc-tuning vs. 对比学习

怀疑论者可能会问: “也许提升仅仅是因为你在第二阶段添加了更多数据？”

为了验证这一点，作者将 Pcc-tuning 与“两阶段对比学习”方法进行了比较。在对比设置中，他们采用相同的第一阶段模型，并继续在第二阶段数据上进行训练，但仍使用对比损失 (将高分对视为正样本) 。

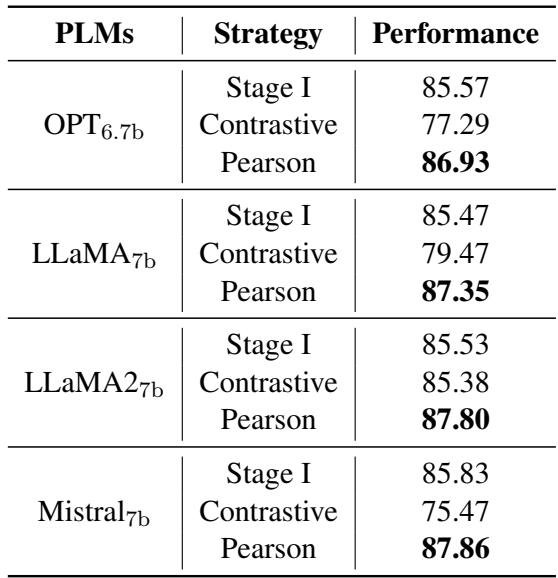
表 3 中的结果截然不同:

• Contrastive (对比学习) : 继续进行对比学习实际上损害了性能 (分数降至约 85.5 或更低) 。这很可能是因为对比学习需要大批次 (Large Batch) 和海量数据才能良好运作。
• Pearson (Pcc-tuning) : 使用皮尔逊损失将性能飙升至 87+ 。

这证明了是方法 (改变损失函数) ，而不仅仅是数据，才是改进的关键。

鲁棒性: 提示词与批次

基于 LLM 的嵌入的一个挫折点是“提示工程” (Prompt Engineering) ——花费数小时寻找完美的短语来触发模型。

Pcc-tuning 似乎对不同的提示词具有高度的鲁棒性。作者测试了三种模板 (PromptEOL, PromptSUM, PromptSTH) 。

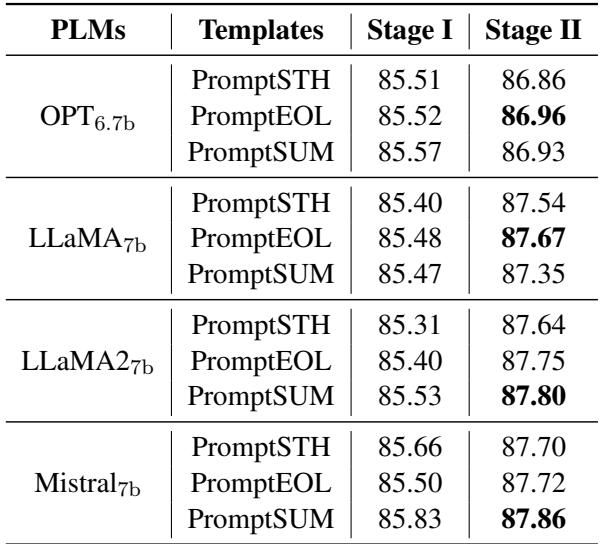
如表 5 所示，无论提示词是要求“总结”、“一个词”还是“某事”，第二阶段的微调 (最右列) 始终产生约 87.3 - 87.8 的分数。

此外，Pcc-tuning 非常高效。对比学习通常需要巨大的批次大小 (例如 512+) 才能找到足够的“困难负样本”。Pcc-tuning 则基于当前批次的相关性进行工作。

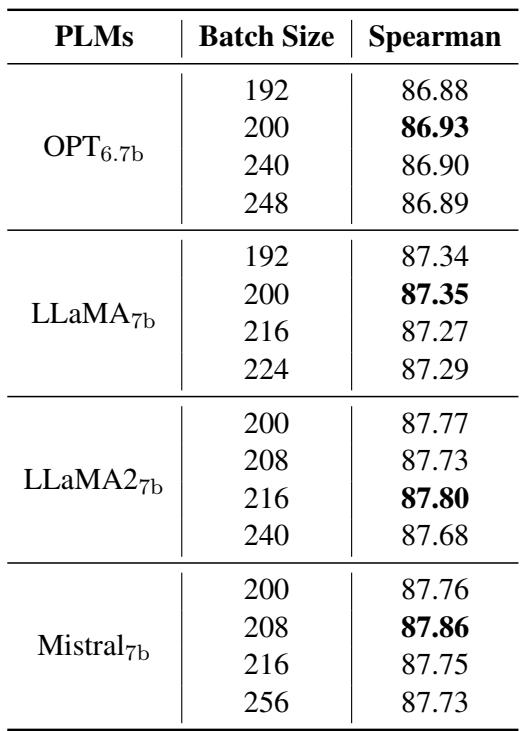
表 8 显示，即使批次大小发生显著变化，Pcc-tuning 仍保持稳定且有效。它所需的内存也更少，因为相关性计算比大批次对比学习所需的巨大矩阵运算在计算上更轻量。

结论: 嵌入的新范式？

论文 “PCC-tuning: Breaking the Contrastive Learning Ceiling in Semantic Textual Similarity” 为 NLP 社区提供了一个令人信服的故事。

1. 诊断: 它指出对比学习虽然强大，但由于将连续问题简化为二元问题，本质上将 STS 性能限制在了 87.5 的分数。
2. 治疗: 它引入了 Pcc-tuning，这种方法将训练目标 (皮尔逊损失) 与评估目标 (相关性) 对齐。
3. 效率: 它仅使用极少量的数据 (不到原始训练集大小的 2%) 用于第二阶段，就取得了破纪录的结果。

对于学生和从业者来说，结论很明确: 损失函数很重要。 当你的模型遇到平台期时，可能不是因为缺乏数据或模型规模不够大——可能是你的训练目标与你的最终目标存在根本性的分歧。通过从二元区分转向连续相关性，Pcc-tuning 解锁了大型语言模型的全部精细化潜力。

如果你正在研究句向量，也许是时候停止单纯地“推拉”向量，开始关注相关性了。