引言

想象一下，你正在辅导一名学生学习微积分。他们毫不费力地解出了复杂的解高斯积分，表现出对高等数学概念的深刻理解。印象深刻之余，你问了一个后续问题: “17 乘以 8 等于多少？”学生一脸茫然地回答: “106。”

你会感到莫名其妙。在人类的认知中，能力通常是分层级的；如果你精通高等微积分，人们理所当然地认为你掌握了基础算术。这就是一致性 (Consistency) 的本质。

然而，像 GPT-4 和 Llama 这样的大语言模型 (LLM) 并不像人类那样思考。虽然它们在法律、医学和编程方面表现出了专家级的能力，但它们却缺乏一种独特的鲁棒性。一篇题为 “Can Large Language Models Always Solve Easy Problems if They Can Solve Harder Ones?” (如果大语言模型能解决难题，它们总能解决简单问题吗？) 的新研究论文探讨了一种具体且反直觉的失败类型: 难易不一致性 (Hard-to-Easy Inconsistency) 。

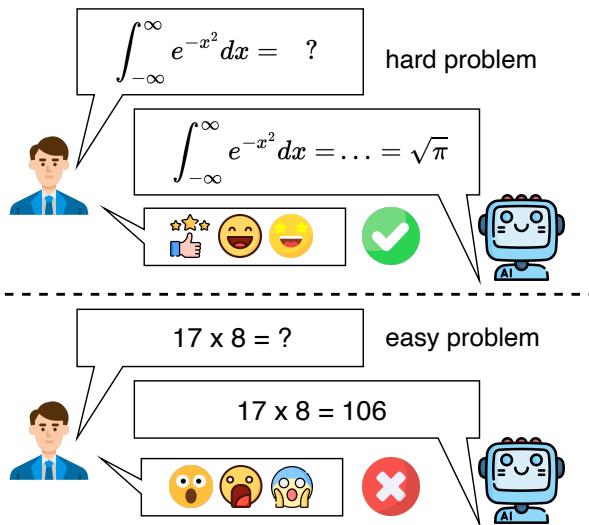
Figure 1: A hard-to-easy inconsistency case of LLMs. A counter-intuitive phenomenon occurs when an LLM, which can solve a harder problem, surprisingly goes wrong on an easier problem.

如上图所示，一个 LLM 可能正确解出一个复杂的积分，却搞砸了一个简单的乘法任务。这篇博客文章将深入剖析这项研究，解释作者如何量化这一悖论、他们创建的基准测试，以及这对未来 AI 可信度意味着什么。

背景: 一致性问题

在剖析新方法之前，我们需要了解 LLM 可靠性的现状。我们知道 LLM 很敏感。先前的研究表明:

  • 语义不一致性 (Semantic Inconsistency) : 稍微改写问题可能会彻底改变模型的回答。
  • 顺序敏感性 (Order Sensitivity) : 改变多选题中选项的顺序会改变预测结果。
  • 逻辑不一致性 (Logical Inconsistency) : 模型可能会同意某个陈述，但不同意其逻辑否定。

这篇论文的作者认为，有一种更根本的不一致性被忽视了。那就是对难度层级 (difficulty hierarchy) 的违反。在一个理性的系统中，解决简单问题所需的技能集应该是解决该问题更难版本所需技能的子集。因此，通过了难题却在简单题上失败，是根本性推理缺陷的标志。

核心方法: ConsisEval

为了科学地研究这一现象，研究人员不能依赖随机问题。他们需要一个受控环境，其中“简单”和“困难”有严格的定义。他们引入了 ConsisEval , 这是一个专门用于测试难易一致性的基准。

1. 构建数据集

ConsisEval 基准涵盖了三个关键领域: 代码、数学和指令遵循 。

与题目相互独立的传统基准不同，ConsisEval 使用成对数据 (pairwise data) 。 每个条目包含一个简单问题 (\(a\)) 和一个困难问题 (\(b\)) 。

  • 严格的难度顺序: 困难问题严格派生自简单问题。它通常包含简单问题作为一个子步骤，或者增加了额外的约束。这确保了在数学逻辑上，如果你能解决 \(b\)，你就拥有解决 \(a\) 的逻辑。

创建过程是 AI 生成与人工监督的混合体:

  1. 种子数据 (Seed Data) : 简单问题取自成熟的数据集 (如用于数学的 GSM8K 或用于代码的 HumanEval) 。
  2. GPT-4 合成 (Synthesis) : 研究人员提示 GPT-4 获取一个简单问题，并通过增加约束或步骤使其“变得更难”，同时确保原始逻辑仍然是新问题的子集。
  3. 人工验证 (Human Verification) : 标注员严格检查这些问题对，以保证难度层级和正确性。

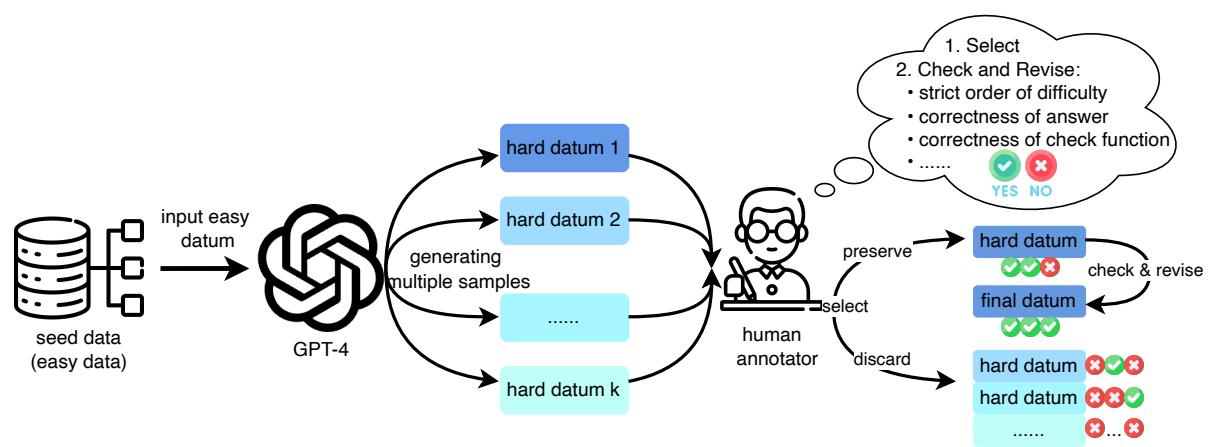
Figure 2: The hard data collection process of ConsisEval. An easy datum is fed into GPT-4 with a wel-esigned prompt and multiple hard data candidates are sampled. Human annotators select the one of best quality,then check and revise the sample to make it fit our criteria.

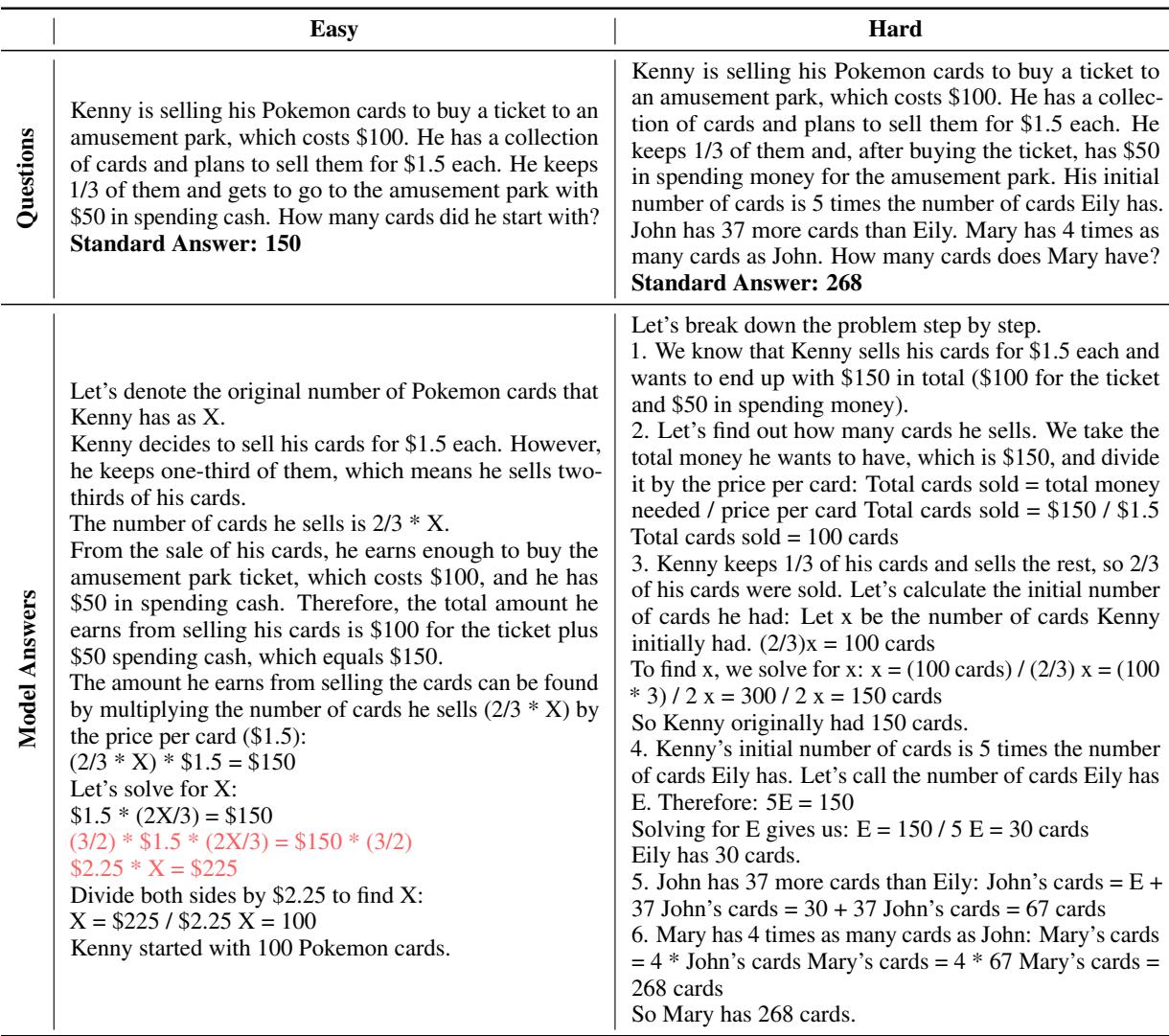
结果是一个问题之间关系明确的数据集。例如，在下表中，请注意“困难”问题 (蓝色文本) 仅仅是在“简单”问题 (绿色文本) 的基础上增加了一层复杂性。

Table 1:An example question pair with a strict order of difficulty. Green text denotes the common part of questions and blue text denotes the additional part of hard question.

2. 定义一致性分数 (CS)

我们如何衡量一个模型是否一致？仅仅看准确率是不够的。我们需要看条件概率。

研究人员将一致性分数 (Consistency Score, CS) 定义为: 在模型已经正确回答了困难问题的情况下，正确回答简单问题的概率。

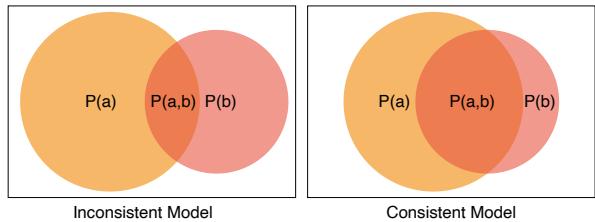
在视觉上，我们可以用维恩图来想象这一点。在一个一致的模型中 (下图右侧) ，代表“解决难题”的圆圈几乎完全包含在“解决简单题”的圆圈内。在一个不一致的模型中 (左侧) ，存在大片区域是模型解决了难题却错过了简单题。

Figure 3: Venn diagram for consistent/inconsistent models in complete probability space. The orange red circles and their overlap area denote the probability of a model correctly answering easy questions,hard questions,and both respectively. the overlap area of consistent models is much larger than that of inconsistent models.

在数学上，一致性分数的计算公式为:

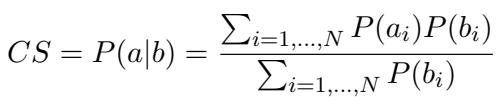
Equation for Consistency Score

或者，在概念上表示为条件概率:

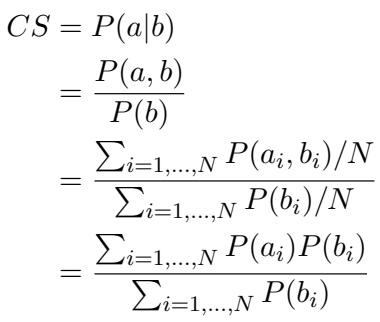
Equation Concept

这里，\(P(a|b)\) 代表在给定困难任务 (\(b\)) 成功的情况下，简单任务 (\(a\)) 成功的可能性。

3. 相对一致性分数 (RCS)

原始的一致性分数有一个陷阱。一个在所有方面都很糟糕的模型 (在简单和困难问题上的准确率均为 0%) 在技术上会有很高的一致性分数，因为它从未遇到“通过难题 / 挂掉简单题”的悖论。但这并没有什么用。

为了解决这个问题，作者引入了相对一致性分数 (Relative Consistency Score, RCS) 。 该指标将模型的一致性与其原始能力联系起来进行评估。

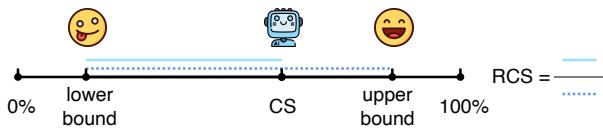
Figure 4: Visualized expression of relative consistency score.

RCS 衡量的是模型处于理论上的“下界” (在其准确率水平下最差的一致性) 和“上界” (最佳的一致性) 之间的位置。

该公式对分数进行了归一化:

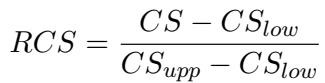
Equation for RCS

为了计算这一点，他们根据模型在数据集上的表现推导出了数学界限。下界 (\(CS_{low}\)) 假设模型在简单和困难问题上的成功是独立的 (随机的) :

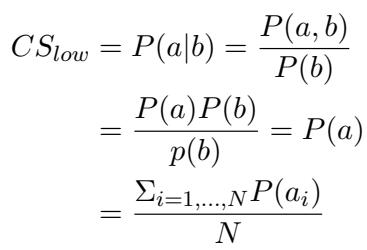
Equation for CS Lower Bound

上界 (\(CS_{upp}\)) 假设模型在给定的难度差距下尽可能地保持一致:

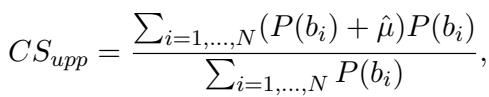
Equation for CS Upper Bound

4. 概率估计

在标准基准测试中，我们通常只问 LLM 一个问题一次 (贪婪解码) ，然后检查它是对是错。然而，LLM 是概率引擎。为了获得准确的一致性分数，我们需要模型解决问题的真实概率 (\(P\)) 。

研究人员使用了采样技术。对于开源模型，他们对答案进行了 20 次采样以估计概率:

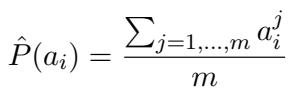
Equation for Probability Estimation

对于昂贵的闭源模型 (如 GPT-4) ，他们使用了一种早停 (Early Stopping) 技术，在保持统计有效性的同时节省成本。一旦发现正确答案，他们就停止采样 (因为高性能模型通常能很快答对) ，概率估计为:

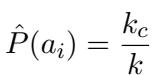
Equation for Early Stopping Estimation

实验与结果

研究人员测试了大量模型，包括 GPT-4、GPT-3.5、Claude-3 Opus、Llama-2/3 和 Qwen。结果提供了当前 AI 可靠性状态的一个迷人快照。

主要发现

下表总结了所有三个领域 (代码、指令、数学) 的表现。

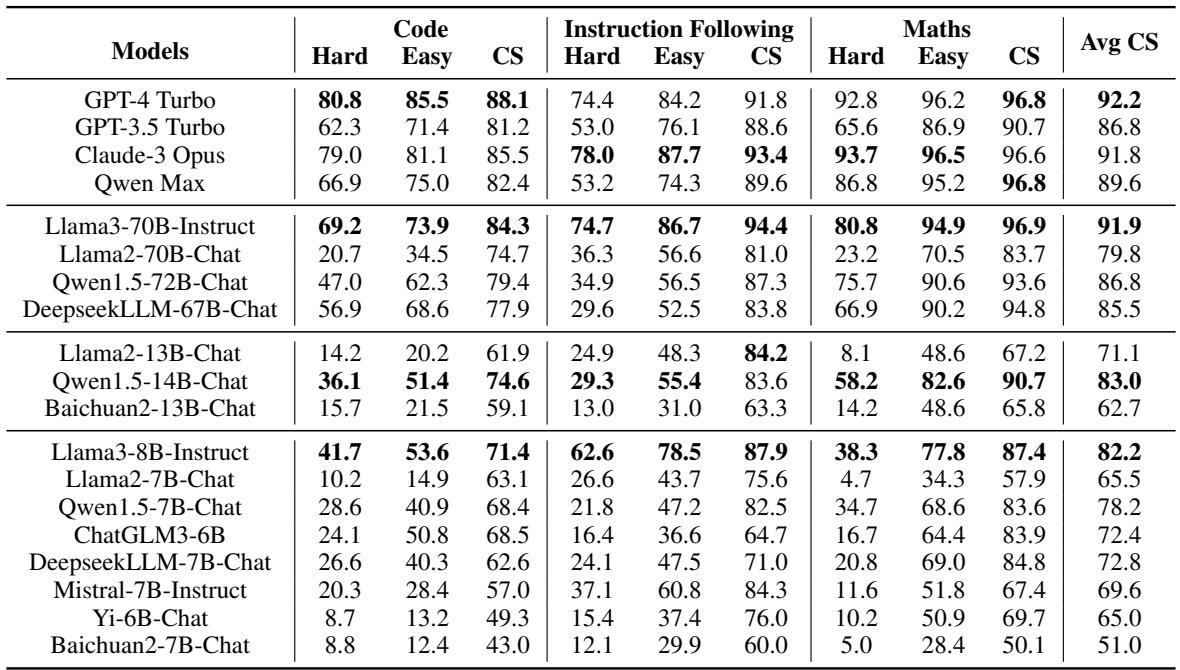
Table 2: Consistency evaluation results. A variety of LLMs are evaluated on code,instruction-following,and maths domains. On each domain,we report consistency score (CS),accuracy \\(( \\% )\\) on hard set and easy set (denoted as Hard and Easy). We also report the average consistency score \\(( \\mathbf { A v g } \\mathbf { C S } )\\) among three domains.

数据中的关键结论:

  1. GPT-4 Turbo 是一致性之王: 它取得了最高的平均一致性分数 (92.2%) 。这表明更强的模型通常在解决问题的层级上更理性。
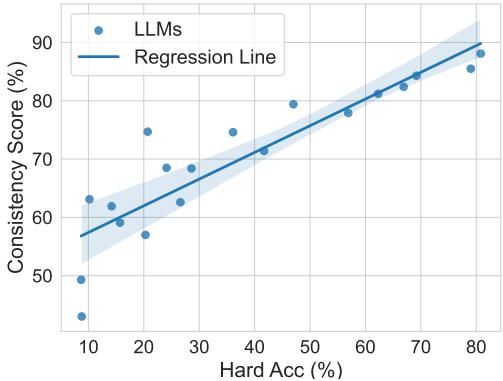
  2. 能力与一致性相关: 模型在难题上的原始准确率与其一致性分数之间存在很强的正相关关系。随着模型变得更聪明，它们往往会犯更少的“愚蠢”错误。 Figure 8: Correlation of capability and consistency.
  3. 存在例外: 有趣的是，Claude-3 Opus 尽管是一个非常强大的模型 (有时在特定数学任务上优于 GPT-4) ，但其一致性分数略低。这证明高准确率并不能自动保证高一致性。

相对一致性分析

当应用相对一致性分数 (RCS) 时，我们要看到即使是最好的模型也有改进的空间。

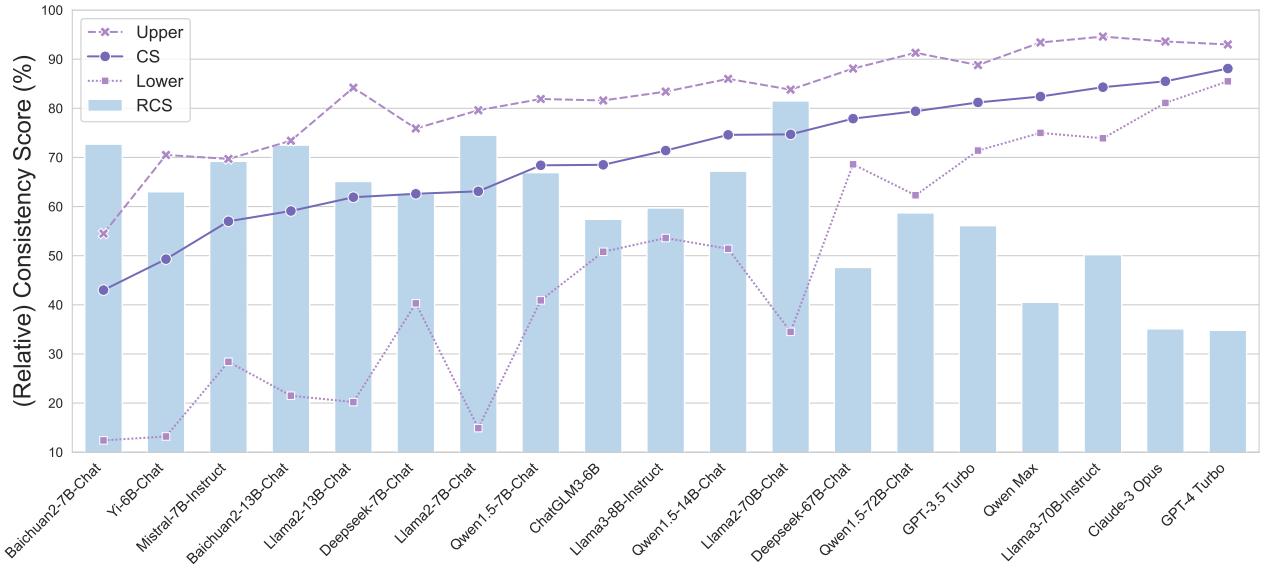
在代码领域 (如下图所示) ，GPT-4 Turbo 拥有很高的原始 CS (88.1%) ，但其 RCS 仅为 34.8%。这意味着相对于其巨大的智能，它在一致性方面仍然表现不佳。它本应该做得更好。相反，像 Llama-2-70B 这样较弱的模型具有较高的 RCS，这意味着尽管它们整体能力较差，但它们非常一致——它们知道自己知道什么，也知道自己不知道什么。

Figure 5: Relative consistency results in code domain (shown in ascending order of CS). Except for showing RCS for each evaluated model in a bar, we also show CS,upper and lower bounds of CS in lines of different colors for comparison.

为什么 LLM 会在简单问题上失败？

数字告诉我们它们确实失败了，但定性分析告诉我们为什么。作者进行了案例研究，分析了 GPT-4 解决了难题却在简单版本上失败的具体实例。

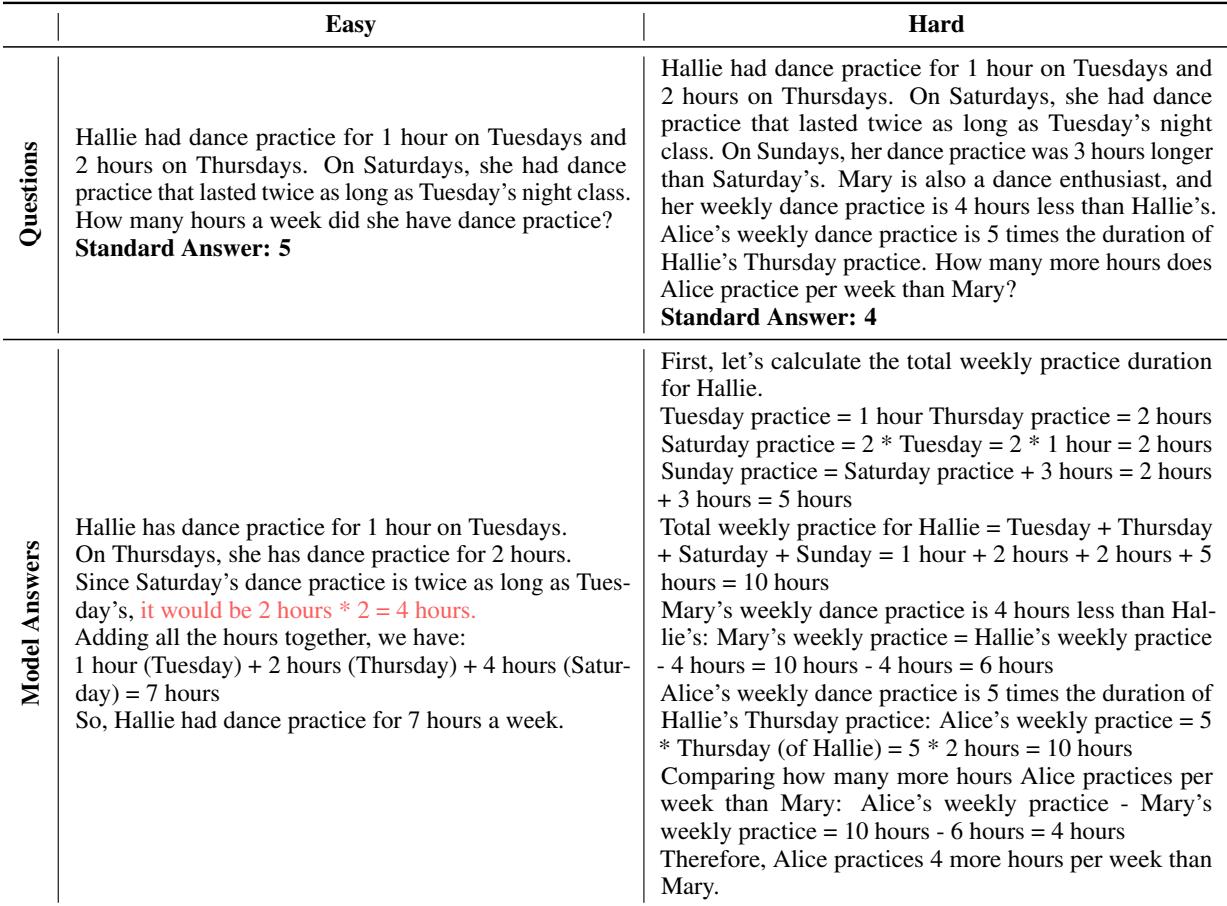
1. 被冗余信息干扰

当简单问题包含“废话”或额外细节时，LLM 经常会陷入挣扎。在下面的例子中，模型被简单提示中提到的“周四 (Thursday) ”搞混了，错误地将其应用到了计算中。

Table 7: An inconsistency case for GPT-4. Red texts denote wrong reasoning steps. Misapplication of data occurs with GPT-4: Tuesday involves 1 hour of dancing,while GPT-4 mistakenly uses Thursday’s 2 hours in its calculation, resulting in a wrong final answer.

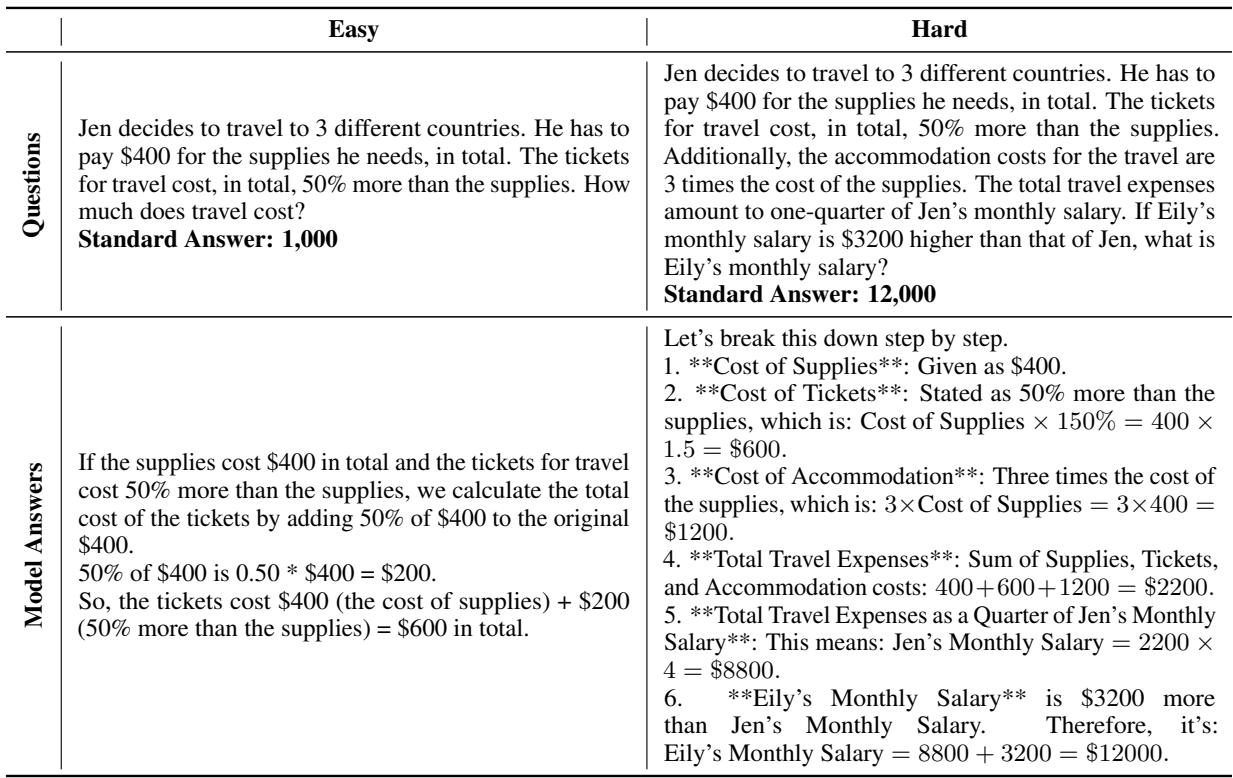
2. 过度思考和误解

有时，模型会预期并不存在的复杂性。在这个旅行费用的例子中，模型正确计算了复杂场景 (困难) ，却误解了简单场景中的简单请求，只计算了机票费用而不是总费用。

Table 8: An inconsistency case for GPT-4. Misunderstanding of the question leads to an error: the question askes for the total cost of the trip,whereas GPT-4 only calculates the cost of travel tickets.

3. 简单的计算错误

矛盾的是，“困难”问题通常迫使模型进入更深层的推理模式 (如思维链) ，这起到了防止错误的护栏作用。简单问题可能会触发一个更快、不太仔细的生成路径，导致基础算术失败。

Table 10: An inconsistency case for GPT-4. Red texts denote wrong reasoning steps. GPT-4 encounters a computational error while solving equations.

启示: 我们该如何修复？

论文最后提出了两项关于如何提高一致性的重要实验。

1. 在更难的数据上训练

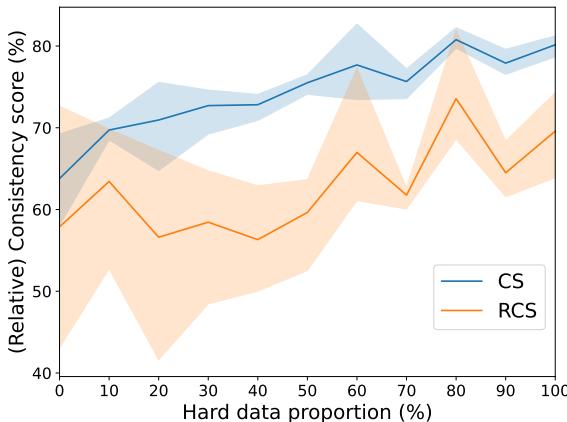
研究人员在具有不同简单与困难数据比例的数据集上微调了模型。结果很明确: 困难数据增强了一致性。

如图 6 所示，随着训练集中困难数据比例的增加 (x 轴) ，一致性分数 (CS) 也随之上升。这表明，让模型接触困难的推理模式比反过来更能向下泛化到简单的任务。

Figure 6: Consistency of models fine-tuned on training sets of different proportions of easy and hard data.Finetuned models show higher consistency with more hard training data.

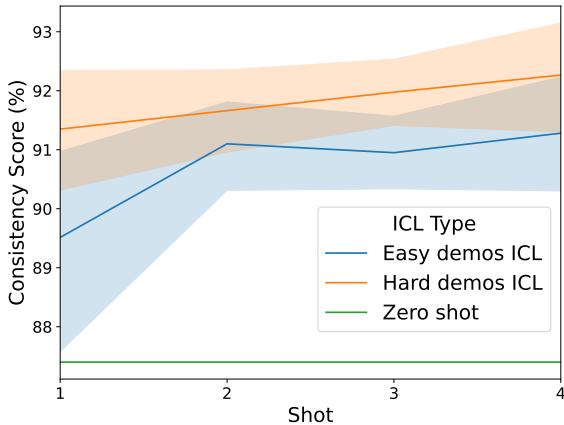
2. 在提示中使用困难示例

对于无法重新训练模型的用户，解决方案在于上下文学习 (In-Context Learning, ICL) 。 当在提示中提供“少样本 (few-shot) ”示例时，使用困难示例比使用简单示例能产生更好的一致性。

Figure 7: Consistency behavior of ICL with easy and hard examples under 1-4 shot settings. ICL with harder examples shows higher consistency.

结论

这篇题为“Can Large Language Models Always Solve Easy Problems if They Can Solve Harder Ones?”的研究强调了人工智能与人类智能之间的一个关键差距。人类构建知识就像金字塔——广泛的简单技能基础支撑着高级能力的顶峰——而 LLM 更像是一座叠叠乐积木塔。它们可以达到令人眩晕的性能高度，但底部积木的缺失使它们出奇地不稳定。

ConsisEval 和 一致性分数 (Consistency Score) 的引入为 AI 社区提供了一个审视模型评估的新视角。它迫使我们不仅要问“模型答对于了多少个问题？”，还要问“模型的表现是否符合逻辑？”

研究结果指明了一条清晰的前进道路: 要构建更值得信赖的 AI，我们不应只专注于解决最难的谜题。我们必须确保在追求天才的过程中，模型不会丢失常识。通过在更难的数据上进行训练并严格对照一致性基准进行测试，我们可以更接近于构建不仅强大而且可靠的 AI。