如果你曾尝试过训练一个“全能”的大型语言模型 (LLM) ，你就知道这有多么艰难。你想要一个既能解数学题，又能写 Python 代码，还能随意聊天并进行逻辑推理的模型。

标准的方法是数据混合 (Data Mixing) 。 你把你所有的数据集——数学、代码、聊天——扔进一个巨大的搅拌机，然后在这个混合后的“汤”上训练模型。问题在于？这种方法极其昂贵，而且众所周知地难以调优。如果你把数学数据和聊天数据的比例搞错了，模型可能会变得极擅长代数，但却忘了怎么说人话。如果你以后想添加一项新技能，你通常不得不重新混合并从头开始训练。

但是，如果你根本不需要混合数据呢？如果你可以在数学数据上训练一个模型，在代码数据上训练一个单独的副本，然后只是简单地利用算术把这些技能……加在一起呢？

这就是一篇引人入胜的新论文 “DEM: Distribution Edited Model for Training with Mixed Data Distributions” (DEM: 用于混合数据分布训练的分布编辑模型) 的前提。研究人员提出了一种方法，比传统训练便宜 11 倍 , 并且在 MMLU 和 BBH 等基准测试中表现显著更好。

在这篇文章中，我们将解构分布编辑模型 (DEM) 是如何工作的，“编辑”模型权重背后的数学原理，以及为什么这种模块化方法可能是 LLM 微调的未来。

问题: “搅拌机”方法的高昂成本

要理解为什么 DEM 是必要的，我们需要先看看现状: 多任务指令微调 。

在构建通用助手时，工程师会收集各种各样的数据集 (\(D_1, D_2, \dots, D_n\)) 。一个数据集可能是思维链 (CoT) 推理，另一个可能是对话。

在标准的数据混合方法中，目标是学习一个涵盖所有这些数据集的联合分布。训练过程会根据特定的权重 (例如，30% 数学，50% 聊天，20% 逻辑) 从每个数据集中采样批次。

这带来了两个巨大的令人头疼的问题:

  1. 超参数噩梦: 你必须找到完美的混合权重。这需要训练多个代理模型或运行昂贵的网格搜索。
  2. 僵化性: 如果你在完成训练后发现忘了一个特定的代码数据集，你不能简单地把它“补丁”进去。你实际上必须重新混合并重新训练。

研究人员认为我们是在自找麻烦。与其强迫模型一次性学习所有东西，不如让它单独学习各项技能，稍后再将它们组合起来。

解决方案: 分布编辑模型 (DEM)

DEM 的核心思想是模块化。我们混合的是模型，而不是混合数据。

该过程分为三个不同的步骤:

  1. 独立微调: 取你的基座模型 (\(\Theta\)) ，并在每个数据集 (\(D_i\)) 上分别对其进行微调，以创建特定模型 (\(\Theta_{D_i}\)) 。
  2. 提取分布向量: 计算微调后的模型与基座模型之间的差值。这个差值代表了所学到的“技能”或“分布”。
  3. 向量组合: 将这些加权后的差值加回到基座模型中。

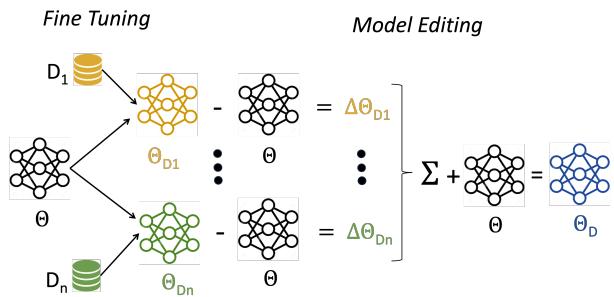
图 1: 分布编辑模型架构。它展示了在 n 个分布上微调基座模型，提取增量向量，并将它们求和的过程。

如图 1 所示，该架构允许采用“即插即用”的方法。你可以在不同的日子、不同的 GPU 上分别训练“数学模型”和“聊天模型”，并在以后将它们组合起来，而无需让原始数据相互接触。

第一步: 模型编辑的数学原理

让我们看看背后的数学，其简单程度令人惊讶且优雅。

首先，对于每个数据集 \(D_i\)，我们获得一个微调后的模型 \(\Theta_{D_i}\)。然后我们计算一个分布向量 (Distribution Vector, DV) , 记为 \(\Delta \Theta_{D_i}\)。这个向量精确地表示了权重是如何变化以学习该特定任务的。

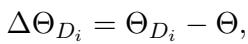
公式 1: 分布向量的计算。

这个操作是逐元素 (element-wise) 进行的。如果基座模型中的某个特定权重是 \(0.5\)，而微调后的模型将其更改为 \(0.7\)，那么该位置的分布向量就是 \(0.2\)。

第二步: 混合配方

一旦我们需要这些向量——我们可以把它们看作是“技能模块”——我们就可以将它们组合起来。最终的分布编辑模型 (\(\Theta_D\)) 是通过将这些向量的加权和加回到原始基座模型来创建的。

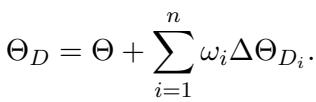
公式 2: 将分布向量组合成最终模型的公式。

在这里，\(\omega_i\) 代表该特定分布的权重 (重要性) 。

这是一个至关重要的优势: 调整 \(\omega_i\) 很便宜。 在旧的“搅拌机”方法中，如果你想改变数学数据集的权重，你必须重新训练模型。在 DEM 中，你只需改变上式中 \(\omega_i\) 的值，基本上就能瞬间将模型“滑动”到更好的数学性能上。不需要梯度下降。

替代方案: 模型插值

作者还讨论了一种称为“模型插值”的细微变体，即直接对微调后的模型进行加权平均。

公式 3: 模型插值的公式，即模型的加权平均。

虽然这个公式 (Eq 3) 看起来很相似，但作者发现分布向量方法 (Eq 2) 提供了更大的灵活性。公式 2 允许模型在某个任务的方向上移动得比任何单个微调模型都“更远”，从而有效地放大所需的特征。

为什么 DEM 便宜这么多？

这里的效率提升是巨大的。让我们分解一下计算成本 (\(c\)) 。

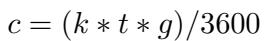
公式 4: 以 GPU 时计算计算成本的公式。

在标准的数据混合场景中，找到最佳组合需要训练许多完整的模型。如果你有 \(n\) 个数据集，并想尝试 \(m\) 种不同的权重组合，复杂度会呈爆炸式增长。

使用 DEM，你训练 \(n\) 个模型 (每个数据集一个) 。组合步骤发生在训练后。你只需要运行验证循环来找到最佳的 \(\omega\) 权重。

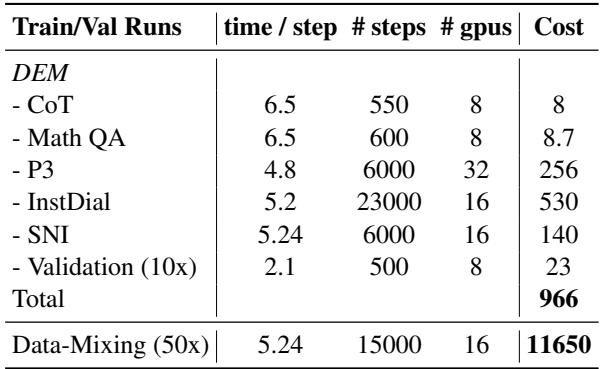
表 8: 训练成本比较，显示 DEM 比数据混合便宜得多。

表 8 中的结果令人咋舌。

  • DEM 总成本: 966 GPU 时。
  • 数据混合成本: 11,650 GPU 时。

DEM 的生产成本大约便宜 11 倍 。 这使得强大的多任务模型的创建变得更加普及，因为它不再需要寻找最佳数据混合所需的大规模计算基础设施。

实验结果: 它真的有效吗？

便宜固然好，但前提是模型性能要好。研究人员使用 OpenLLaMA (7B) 作为基座，在多种数据集上微调并测试了 DEM，包括:

  • P3: 大量的提示任务集合。
  • Super Natural Instructions (SNI): 1,616 个不同的 NLP 任务。
  • 思维链 (CoT): 推理任务。
  • MathQA: 数学应用题。
  • InstructDial: 对话任务。

下游任务性能

他们在 MMLU (知识) 、BBH (推理) 和 DROP (阅读理解) 等基准上评估了模型。

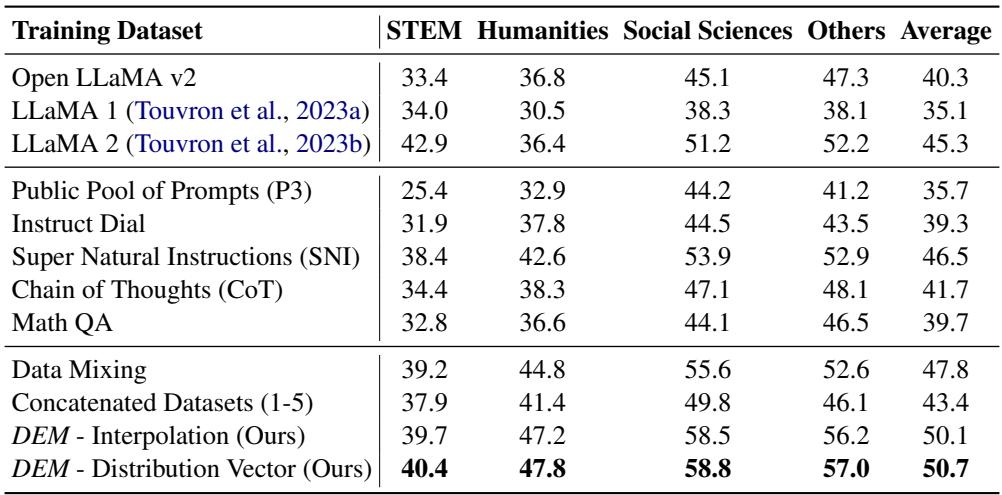
表 11: MMLU 领域特定任务性能。DEM 在 STEM、人文和社会科学领域均优于基线。

表 11 突显了 DEM 的优势。

  • OpenLLaMA 基座: MMLU 平均分 40.3%。
  • 数据混合 (昂贵的基线) : 47.8%。
  • DEM (分布向量) : 50.7% 。

DEM 不仅击败了基座模型 (这是预期的) ，而且在 MMLU 上比经过高度调优的数据混合基线高出近 3 个百分点。这种模式在其他基准测试中也同样存在。

HELM 评估

研究人员还运行了语言模型整体评估 (HELM) ，这是一个检查多样化能力的严格标准。

表 3: HELM 评估的汇总结果。DEM 在 6 个类别中的 5 个获胜。

如表 3 所示，DEM 在分类、OpenBook QA、推理和对话任务中优于数据混合。这证明了通过向量算术将模型“缝合”在一起不会导致产生一个“弗兰肯斯坦式”的怪物模型；相反，它产生了一个连贯的、有能力的通才。

它可以扩展吗？

LLM 研究中的一个常见问题是: “这是否只适用于小模型？” 作者在 3B、7B 和 13B 参数的模型上测试了 DEM。

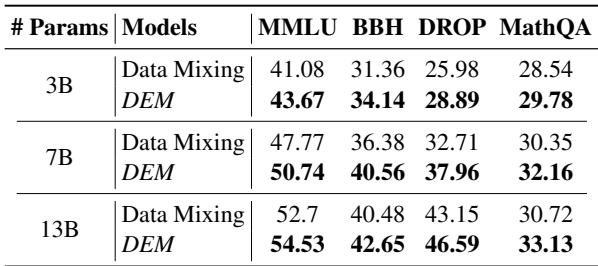
表 4: 模型大小对性能的影响。改进在 3B、7B 和 13B 模型中是一致的。

表 4 证实了该技术的可扩展性。无论是在 3B 还是 13B，DEM 始终优于数据混合。例如，在 13B 模型上，DEM 在 DROP 上获得了 46.59 分，而数据混合为 43.15 分。

为什么这行得通？深入探究

仅仅把权重加在一起就能如此有效，这感觉有点反直觉。为什么“数学权重”不会覆盖“聊天权重”并毁掉模型？

研究人员对此进行了详尽的分析，重点关注向量的几何结构。

1. 任务的正交性

他们计算了不同数据集的分布向量之间的余弦相似度 。

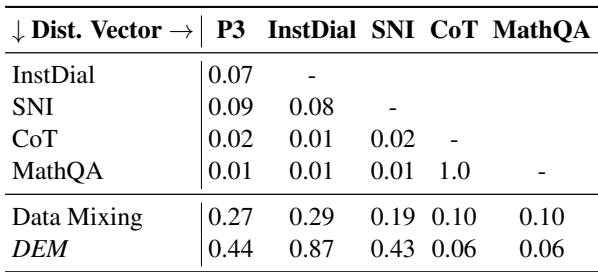
表 7: 分布向量之间的余弦相似度。大多数接近于零。

表 7 揭示了一个迷人的属性: 大多数分布向量几乎是正交的 (相似度 \(\approx 0\)) 。

  • CoT (推理) 的向量与 InstructDial (聊天) 几乎没有重叠。
  • MathQA 与 SNI 也是截然不同的。

这意味着学习数学让模型的权重移动的方向与学习对话完全不同。因为这些向量在高维参数空间中指向不同的方向，你可以将它们加在一起而不会相互干扰。这就是为什么当你添加数学模块时，模型不会“忘记”如何聊天的数学原因。

2. 任务分离

为了将其可视化，作者使用 t-SNE (一种用于可视化高维聚类的技术) 绘制了数据。

图 2: 微调数据集的 tSNE 表示，显示了明显的聚类。

图 2 直观地证实了余弦相似度数据。数据集形成了独特、分离的簇 (CoT 和 MathQA 之间有一些轻微的重叠) 。这种分离表明，这些任务所需的“技能”依赖于不同的特征，使得向量加法策略能够干净利落地工作。

3. 逐层分析

这些“编辑”实际上发生在哪里？作者逐层分析了基座模型与微调模型之间的欧几里得距离。

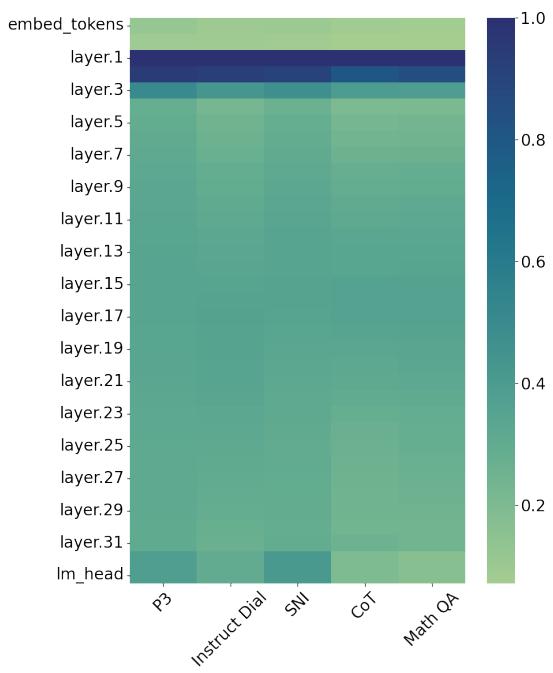
图 3: 逐层欧几里得距离比较。变化集中在早期层。

图 3 显示了一些令人惊讶的事情。大部分繁重的工作发生在最初的几层 (热图顶部的深色区域) 。后面的层保持相对稳定。这表明微调主要适应了模型如何处理和嵌入基本特征，而不是重写位于中间/后期层的深度推理回路。这种变化的局部化可能是合并模型如此具有非破坏性的另一个原因。

增量学习的力量

DEM 最有力的论据之一不仅仅是性能——而是灵活性 。

在传统的流程中，如果你想提高模型的数学分数，你必须用更多的数学数据从头开始整个大规模训练。有了 DEM，你可以简单地:

  1. 仅在新的数学数据上训练一个模型。
  2. 提取向量。
  3. 将其添加到你现有的 DEM 中。

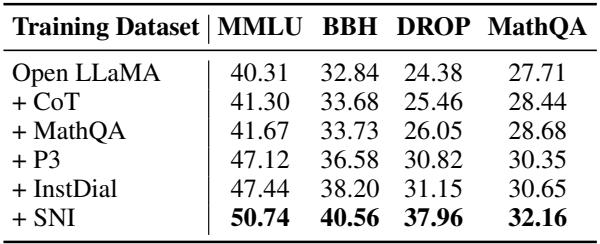
表 5: 逐步添加分布向量的效果。性能逐步提高。

表 5 展示了这种能力。作者从基座模型开始，逐步逐个添加向量 (+CoT, +MathQA, +P3…) 。每次添加，MMLU 分数都会上升。这允许增量升级 , 这对于全面重新训练成本过高的生产环境至关重要。

结论

“分布编辑模型” (DEM) 论文挑战了 LLM 必须同时在所有数据上训练才能学习多项任务的假设。通过将微调模型视为参数空间中的向量，作者证明了我们可以对“技能”进行算术运算。

关键要点:

  • 效率: 与数据混合相比，DEM 将训练成本降低了 90% 以上。
  • 性能: 通过允许对每个数据源进行专门优化，它在主要基准测试中取得了更高的分数。
  • 模块化: 任务很大程度上是正交的，允许我们叠加技能而不会产生灾难性的干扰。

随着我们迈向更大的模型和更多样化的数据，像“编辑”而不是“重新训练”模型的能力可能会成为 AI 工程师工具箱中的标准部分。DEM 预示着这样一个未来: 我们不只是训练模型；我们在组合它们。