引言

在计算科学的世界里，模拟现实就像一种平衡的艺术。无论是预测天气、设计空气动力学汽车，还是模拟结构应力，科学家们都依赖于 有限元方法 (FEM) 。 这些方法将复杂的物理形状分解为由简单的形状 (三角形或四面体) 组成的网格，称之为 网格 (mesh) 。

FEM 的黄金法则很简单: 网格中的点 (或节点) 越多，模拟就越精确。然而，更多的点意味着显著增加的计算成本。在一个粗糙网格上只需几分钟的模拟，在密集网格上可能需要数周。

这就产生了一个根本性问题: 我们如何在不引爆计算预算的情况下实现高精度?

答案在于 网格自适应 (Mesh Adaptivity) 。 与其在所有地方均匀地增加点，不如移动现有的点，将它们集中在模拟最复杂的区域 (如激波或湍流涡旋) ，并在变化不大的区域将它们分散开。

今天，我们将深入探讨一篇开创性的论文，题为 “G-Adaptivity: optimised graph-based mesh relocation for finite element methods” (G-Adaptivity: 用于有限元方法的优化图基网格重定位) 。作者提出了一种利用 图神经网络 (GNNs) 解决这一问题的新方法。与以前试图模仿经典数学求解器的机器学习尝试不同，这种方法通过 直接最小化模拟误差 来学习移动网格点。

让我们先直接看看性能差异。

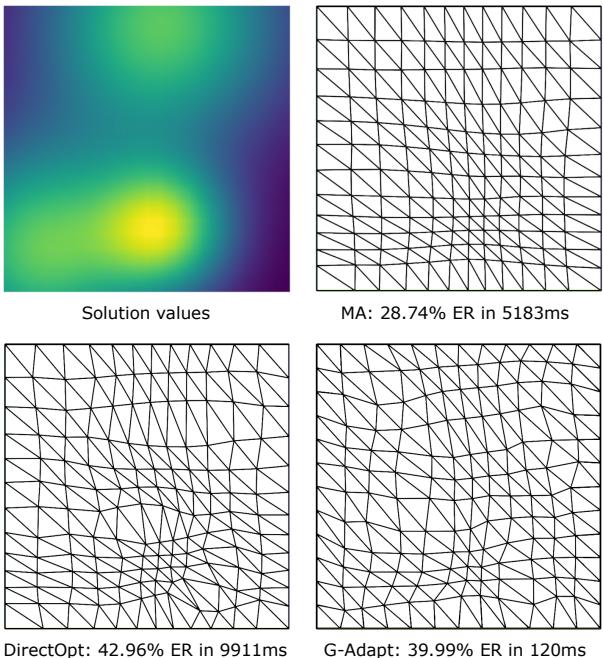
图 1. 我们的新方法 (G-Adapt) 在泊松方程示例上的优化网格。G-Adapt 实现了与经典蒙日-安培方法几乎相同的精度 (约 40% 的误差缩减) ，但速度快了 40 多倍。

如上所示，新方法 (G-Adapt) 实现了与黄金标准数学方法 (蒙日-安培或 MA) 相当的误差缩减，但运行速度却只有后者的零头 (120毫秒 vs 5183毫秒) 。

在这篇文章中，我们将详细解析 G-Adaptivity 的工作原理，它为何能防止常见的网格“纠缠” (tangling) 问题，以及它在流体动力学等复杂物理问题上的表现。

背景: 对完美网格的追求

要理解 G-Adaptivity 为何如此重要，我们需要先了解它所解决的数学问题。

PDE (偏微分方程) 背景

我们试图求解偏微分方程 (PDEs)。抽象地说，我们在寻找像这样的方程的解 \(u\):

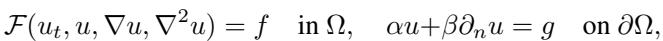
抽象 PDE 形式

当我们使用 FEM 进行数值求解时，我们会得到一个近似解 \(U_{\mathcal{Z}}\)。我们的目标是最小化真实物理量 \(u\) 与我们的近似值 \(U_{\mathcal{Z}}\) 之间的误差。这通常通过平方 \(L^2\) 误差来衡量:

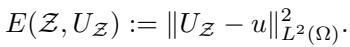
L2 误差方程

r-自适应: 移动网格

适应网格主要有两种方式:

  1. h-自适应: 将现有的三角形切割成更小的三角形。这会改变点的数量和数据结构，计算上会比较麻烦。
  2. r-自适应 (重定位) : 保持点的 数量 不变，但移动它们的坐标。这是本文关注的重点。

在经典方法中, r-自适应 被视为一个“均分” (equidistribution) 问题。想象你有一个“监控函数” \(m(\mathbf{z})\)，它告诉你哪里误差大。你希望排列网格点，使误差在所有单元格中平均分布。

最先进的经典方法涉及求解 蒙日-安培 (MA) 方程 :

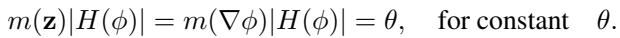
蒙日-安培方程

求解这个方程可以确保得到高质量且不“纠缠” (即三角形不翻转或重叠) 的网格。然而，求解 MA 方程实际上是为了给你的 实际 PDE 设置网格而求解 另一个 非线性 PDE。这既慢又计算昂贵。

机器学习代理陷阱

最近加速这一过程的尝试使用了机器学习来学习蒙日-安培方程的“代理模型”。他们训练一个神经网络来预测 MA 求解器 会 做什么。

虽然速度更快，但这种方法有一个上限: 它永远不会比它所模仿的 MA 方法更好。它继承了经典方法的局限性，而没有从根本上重新思考优化目标。

核心方法: G-Adaptivity

G-Adaptivity 的作者采取了不同的路线。他们没有问 “蒙日-安培方程会把这些点放在哪里？”，而是问:

“这些点应该去哪里才能直接最小化有限元误差？”

这是一个微妙但强有力的转变。它将网格生成变成了一个优化问题，其中的损失函数就是实际的物理模拟误差。

1. 架构: 图与特征

网格被视为一个 图 (Graph) , 其中网格点是节点，连接它们的线是边。模型使用 图神经网络 (GNN) 来处理这些数据。

网络的输入是一个特征矩阵 \(\mathbf{X}\)。关键是，这个矩阵包括:

  1. 网格点的坐标。
  2. 当前解的 海森矩阵 (Hessian) (曲率) 。曲率高的区域通常意味着高误差，需要更多的网格点。

2. Diffformer: 基于扩散的变形器

架构中最具创新性的部分是它如何决定移动点。简单地预测新坐标 (\(x, y\)) 是危险的——网络很容易意外预测出相互交叉的坐标，导致网格“纠缠”并使模拟崩溃。

为了解决这个问题，作者引入了 Diffformer 。 网格点不是直接跳到新位置，而是遵循扩散过程在“伪时间” \(\tau\) 内演变。

移动由速度方程控制:

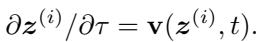
基于速度的网格移动

在 G-Adaptivity 框架中，该速度由图上的可学习扩散过程决定:

扩散方程

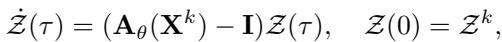
在这里，\(\mathbf{A}_{\theta}\) 是一个学习到的“注意力”矩阵，描述了连接的节点之间相互拉扯的强度。

架构流程

让我们通过可视化来看看整个过程:

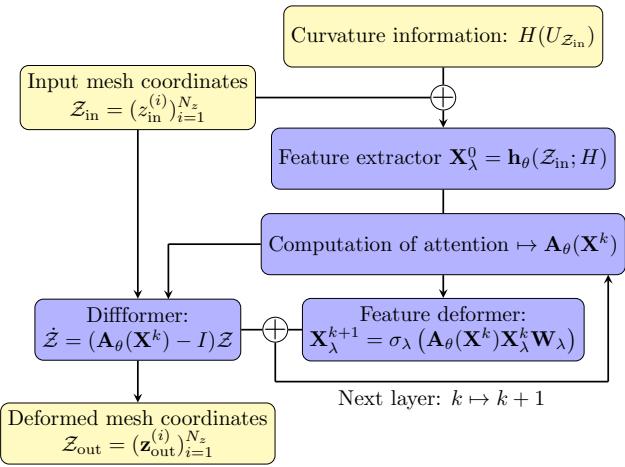
图 2. 我们新的基于图扩散的架构示意图。

  1. 输入: 我们从当前的网格坐标和解的曲率 (海森矩阵) 开始。
  2. 注意力: 网络计算一个注意力矩阵 \(\mathbf{A}_{\theta}\)。这决定了图中边的“权重”。
  3. 扩散: 通过求解扩散方程 (“Diffformer”模块) 来更新网格坐标。
  4. 循环: 这可以分层 (块) 重复进行，以细化移动。

3. 为什么它不会纠缠

网格纠缠是 r-自适应的噩梦。当一个节点移动到其邻居形成的单元之外，导致三角形重叠时，就会发生纠缠。

Diffformer 通过设计防止了这种情况。因为移动是基于图扩散的，每个节点实际上都被拉向其邻居的加权平均值。

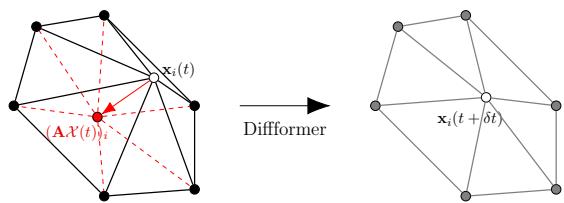
图 3. 图扩散的作用将节点拉入其图邻居的凸包中。

如 图 3 所示，扩散过程将节点 \(\mathbf{x}_i\) 拉入其邻居的 凸包 (convex hull) (几何上的“安全区”) 。

作者提供了一个定理，证明如果扩散的时间步长足够小 (\(dt < 1/2\))，网格在数学上保证不会纠缠。

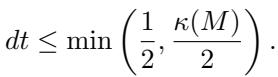
非纠缠时间步长条件

4. 通过直接优化进行训练

网络如何学习最优的 \(\mathbf{A}_{\theta}\)？

这正是该论文利用现代可微分编程的地方。他们使用 Firedrake , 一个自动化的 FEM 系统。因为 Firedrake 可以通过物理模拟本身计算梯度 (导数) (使用伴随法) ，系统可以精确计算移动网格点 \((x, y)\) 如何影响最终误差。

用于训练的损失函数由两部分组成:

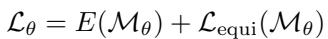
总损失函数

  1. \(E(\mathcal{M}_{\theta})\) : 实际的有限元误差 (物理误差) 。
  2. \(\mathcal{L}_{\mathrm{equi}}\) : 一个“均分”正则化项。

正则化项有助于稳定训练，通过鼓励网格尊重经典理论中的“监控函数”概念，即使在主要目标直接最小化误差的同时。

均分损失

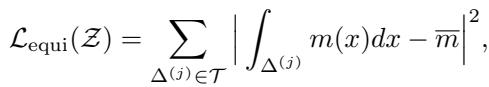
实验与结果

研究人员在几个标准的物理问题上测试了 G-Adaptivity。

1. 泊松方程 (稳态)

泊松方程是 FEM 的“Hello World”。他们在正方形域和复杂的多边形域上进行了测试。

表 1 显示了结果。 G-Adapt 实现了比经典蒙日-安培 (MA) 方法和之前的 ML 最先进技术 (UM2N) 显著更高的误差缩减 (ER)。

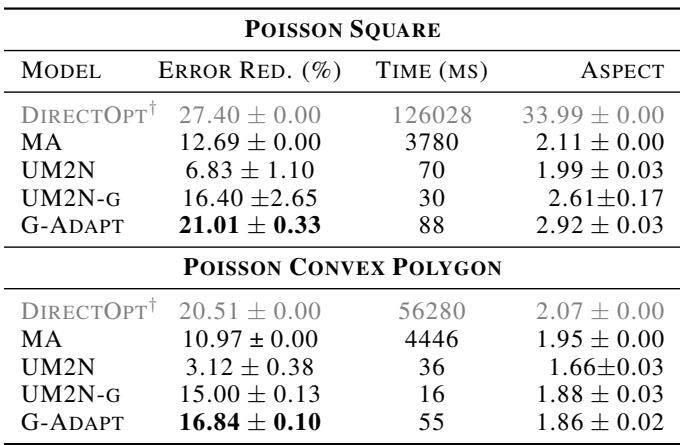
表 1. 泊松正方形和泊松凸多边形数据集的基准测试结果。

  • 正方形域: G-Adapt 达到了 21.01% 的误差缩减 (ER)，击败了 MA (12.69%) 和 UM2N (6.83%)。
  • 速度: 它的运行时间为 88ms , 相比之下 MA 为 3780ms 。

该方法在不规则形状上也表现出色。下图是为多边形域生成的网格。注意三角形是如何在解强度高的区域 (左侧的黄点) 周围收缩 (细化) 的。

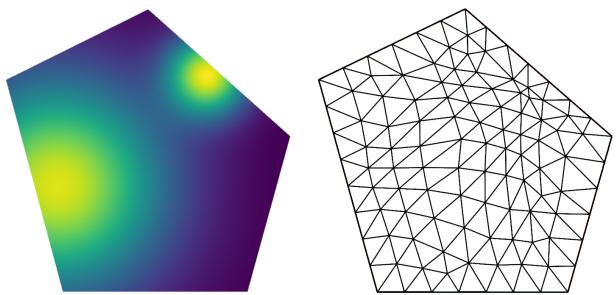
图 4. 多边形域上的解场和相应的 G-Adaptive 网格。

2. 伯格斯方程 (含时)

伯格斯方程涉及随时间移动的波。这更难，因为网格需要随着波的移动而演变。

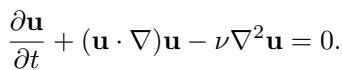
伯格斯方程

作者测试了一个“推演”场景，模拟了 20 个时间步长。

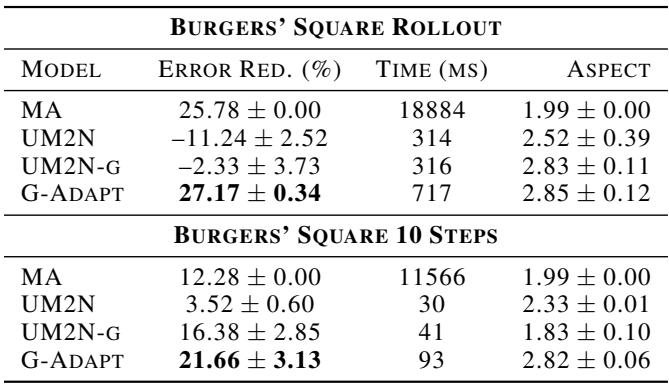
表 2. 伯格斯正方形数据集的基准测试结果。

表 2 中的结果令人震惊。之前的 ML 基线 (UM2N) 实际上 增加 了误差 (负缩减) ，可能是因为它无法处理波的分布变化。 G-Adapt 保持稳定，实现了 27.17% 的误差缩减，略微击败了昂贵的经典 MA 方法。

下面的可视化展示了网格随时间跟踪速度场的情况。

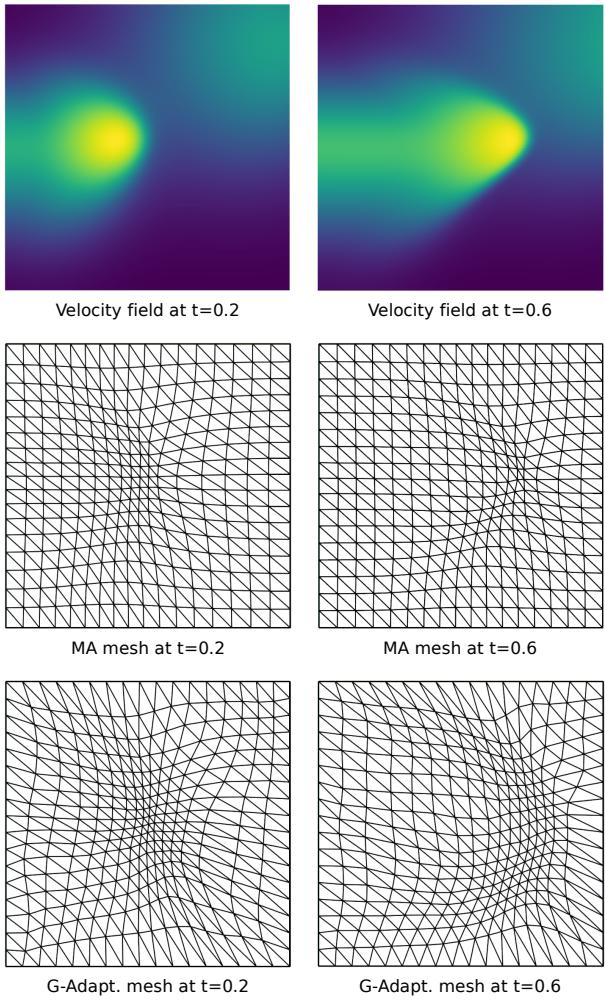
图 5. 伯格斯方程的速度场快照和变形网格。

3. 纳维-斯托克斯 (流体动力学)

这些实验的终极挑战是纳维-斯托克斯方程，模拟流过圆柱体的流动。这涉及复杂的相互作用，如涡旋脱落 (物体后方的旋流) 。

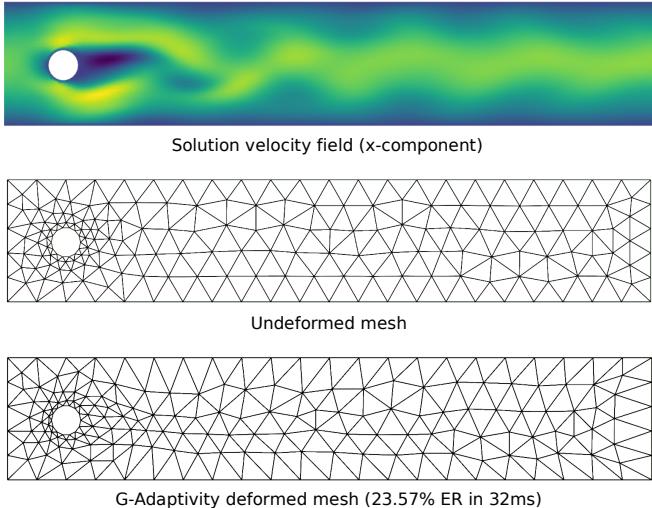
图 6. 纳维-斯托克斯方程上的 G-Adaptivity 变形网格。

在 图 6 中，你可以看到网格自动细化:

  1. 在流体撞击物体的“驻点” (圆柱体前方) 。
  2. 在圆柱体后方形成涡旋的“尾流”中。

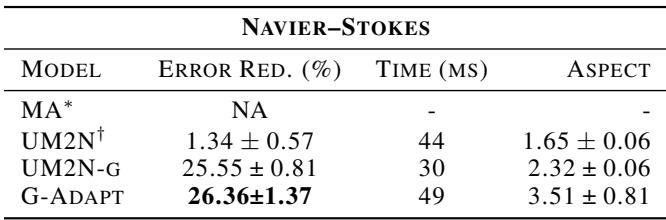
表 3 证实 G-Adaptivity 仅需 49ms 就能实现 26.36% 的误差缩减。

表 3. 纳维-斯托克斯数据集的基准测试结果。

4. 3D 与可扩展性

最后，作者展示了他们方法的基于图的性质使其能够轻松扩展到 3D 以及比训练时大得多的网格 (超分辨率) 。

这是一个 3D 立方体网格适应中心热源的例子。

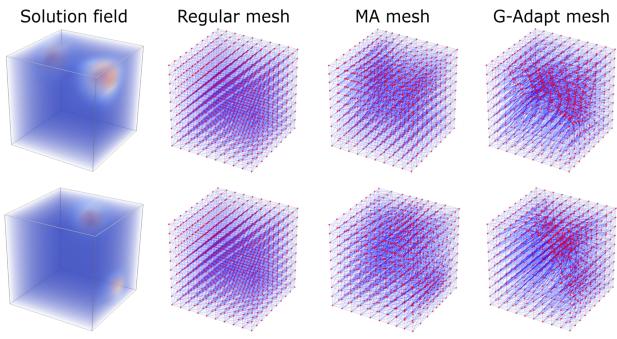
图 7. 3D 解场和适应网格的示例。

这里展示了该方法尽管是在较粗糙的网格上训练的，却能扩展到精细网格 (150x150)。

图 8. 大规模精细网格上的 G-Adaptivity

结论

“G-Adaptivity” 论文代表了科学计算领域迈出的重要一步。通过结合 图神经网络 的几何直觉与 有限元方法 的严谨数学，作者创造了一种工具，它:

  1. 快: 比求解蒙日-安培方程快几个数量级。
  2. 准: 直接最小化物理误差，而不仅仅是模仿旧的启发式方法。
  3. 稳: 使用基于扩散的架构，在数学上保证网格不会破坏。

这种方法——使用可微分物理求解器来训练神经网络以优化模拟参数——很可能是高性能计算的未来。它让我们从纯粹的数据驱动的“黑盒”转向尊重物理定律并利用 AI 速度的“灰盒”模型。