AI 心灵的永恒阳光：大语言模型定向遗忘的因果视角

想象一下，你训练了一个基于整个互联网的大型语言模型 (LLM) 。它聪明、能干且流利。但有一个问题: 它记住了某位随机公民的私人医疗记录，或者知道了你不再拥有使用权的系列小说的版权情节转折。

你不能简单地在神经网络内部点击“删除”特定文件。信息散布在数十亿个参数中。从头重新训练模型虽然能有效移除数据，但这需要数百万美元并且耗时数月。

这就是机器遗忘 (Machine Unlearning) 的挑战。

在这篇文章中，我们将深入探讨一篇引人入胜的研究论文，题为 “Revisiting Who’s Harry Potter: Towards Targeted Unlearning from a Causal Intervention Perspective” (重访“谁是哈利·波特”: 从因果干预视角迈向定向遗忘) 。作者回顾了一种名为“谁是哈利·波特” (Who’s Harry Potter, WHP) 的古怪但有潜力的方法，并利用因果推断 (Causal Inference) 的严谨数学体系对其进行重构。通过这样做，他们不仅解释了该方法为什么有效，还对其进行了大幅改进，使我们能够像外科手术一样从 LLM 中移除特定知识，而无需对其进行“脑叶切除术”。

问题所在: 定向遗忘

在修复模型之前，我们必须定义“修复”意味着什么。在 LLM 的语境下，我们寻求的是定向遗忘 (Targeted Unlearning) 。

大多数当前的遗忘尝试都是“钝器”。它们通常使用像*梯度上升 (Gradient Ascent) *这样的技术——本质上是反向运行训练，以最大化我们想要遗忘的数据上的误差。虽然这擦除了数据，但它往往会破坏模型连贯说话的能力，或者导致它遗忘不相关的信息 (这种现象被称为“灾难性遗忘”) 。

定向遗忘有一个更精细的目标。如果我们想让模型忘记某个特定的人，比如德国历史学家 Wilhelm Wattenbach，我们希望发生三件事:

1. 遗忘目标: 如果被问到“Wattenbach 出生在哪里？”，模型应该不知道。
2. 保留相关知识: 如果训练数据提到 Wattenbach 出生在 Rantzau 镇，模型应该仍然知道 Rantzau 是德国的一个城镇。它只是应该忘记 Wattenbach 和 Rantzau 之间的联系。
3. 保持通用能力: 模型应该仍然能够编写代码、总结诗歌并回答有关埃隆·马斯克的问题。

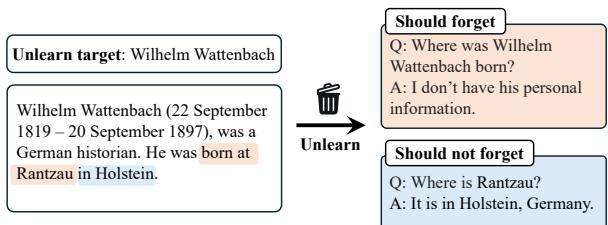
如图 2 所示，目标非常精确。我们要切断实体 (Wattenbach) 与其传记事实之间的联系，而不从模型的“世界观”中删除事实本身。

背景: 谁是哈利·波特？

为了解决这个问题，研究人员回顾了微软研究员 Eldan 和 Russinovich 引入的一种开创性方法，著名的 “谁是哈利·波特” (WHP) 。

WHP 背后的直觉极其简单。为了让 LLM 忘记哈利·波特，你不只是因为提到“哈利·波特”而惩罚它。相反，你创建一个拥有扭曲现实观的“教师”模型。你取原始训练文本，将名字“Harry Potter”替换为一个通用名字 (如“Jon”) ，然后看模型对“Jon”预测什么。

因为模型不知道“Jon”是一个去霍格沃茨的巫师，它会预测通用的补全内容。然后，你训练一个“学生”模型 (即你想要进行遗忘操作的模型) ，让它在看到“Harry Potter”时模仿这种通用行为。

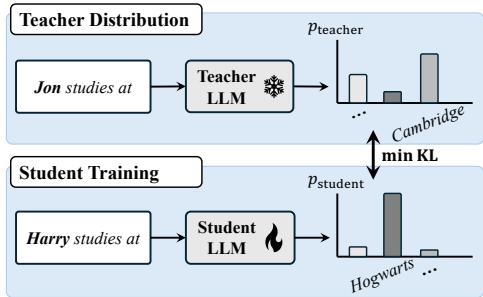
图 1 展示了这种动态。教师分布 (顶部) 看到名字“Jon”并预测一个通用的地点 (如 Cambridge) 。学生 (底部) 最初将“Harry”与“Hogwarts”联系起来。遗忘过程强制学生将其概率分布与教师对齐。

虽然 WHP 是一个突破，但它是启发式的——一个没有坚实数学解释的聪明小技巧。正因如此，它存在缺陷。遗忘后的模型经常产生幻觉或给出不一致的答案。我们要讨论的这篇论文的作者决定使用因果干预将这一过程形式化，将“聪明的小技巧”转变为有原则的算法。

核心方法: 通过因果干预进行遗忘

这是论文的核心部分。要理解如何移除知识，我们必须对知识最初是如何进入模型进行建模。作者提出了一个结构因果模型 (Structural Causal Model, SCM) 。

1. 因果图

让我们把关于一个人的句子生成过程想象成一个因果图。我们有三个变量:

• \(X\) (输入) : 给 LLM 的提示 (例如，“Wilhelm Wattenbach was born in…”) 。
• \(Y\) (输出) : LLM 生成的补全 (例如，“…1819”) 。
• \(E\) (知识) : 模型中存储的底层“事实”或实体知识 (例如，Wattenbach 的传记数据) 。

在标准的 LLM 生成中，知识 (\(E\)) 充当混杂因素 (confounder) 。 它同时影响输入 (我们询问 Wattenbach 是因为他存在) 和输出 (我们得到正确的日期是因为模型知道它) 。

在图 3 中，请看箭头。有一条从 \(X\) 到 \(Y\) 的直接路径 (语言结构) ，和一条通过 \(E\) 的间接路径 (事实知识) 。我们想要打破的“链接”就是 \(E\) 对 \(Y\) 的影响。

2. 干预 (\(do\)-算子)

在因果推断中，如果我们想看看移除某个变量的影响会发生什么，我们使用 \(do\)-算子。我们想要估计 \(P(Y | do(X=x))\)。

从概念上讲，询问 \(P(Y | do(X=x))\) 意味着: “如果我们强制输入为 \(x\)，但切断与特定实体 \(E\) 的联系，模型对这个输入 \(x\) 会预测什么？”

如果我们切断与 Wattenbach 特定知识的联系，模型应该只依赖直接路径——即英语语言的一般统计规律。它应该预测对于任何普通人来说最可能的内容，而不是专门针对 Wattenbach。

在数学上，这使用了后门调整公式:

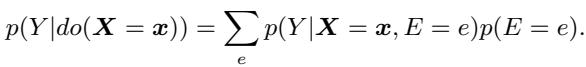
这个公式说: 为了得到“遗忘后”的分布，我们需要对知识 \(e\) 的所有可能值 (例如，所有随机人的传记) 进行求和，并按其概率加权。

3. 用名字交换创造“平行宇宙”

这是该数学原理的一个绝妙的实践实现。我们无法访问神经网络黑盒内部的抽象变量 \(E\)。但是，我们可以通过更改主体的名字来模拟 \(E\) 的不同值。

如果我们将输入中的“Wilhelm Wattenbach”替换为“Alan Turing”，我们实际上是在采样一个不同的 \(e\) (不同的知识) 。如果我们将它替换为“Jon Doe”，我们又采样了另一个。

作者提出了一个三步过程来构建学生应该模仿的教师分布 (Teacher Distribution) :

步骤 1: 更名 (反事实输入) 获取遗忘文档 (例如，Wattenbach 的维基百科页面) 。将每一个“Wilhelm Wattenbach”替换为不同的名字，比如“Paul Marston”。

• *输入: * “Paul Marston was born in…”

步骤 2: 反事实提示 将此修改后的文本输入到冻结的原始 LLM 中。至关重要的是，显式提示模型将其视为 Paul Marston 的传记。这迫使模型使用其关于“Paul Marston”的内部知识 (如果名字未知，则使用通用知识) ，而不是 Wattenbach。

步骤 3: 反向交换 (修正) 这是相对于原始 WHP 方法的一个关键创新。模型将生成对 Paul Marston 的预测。

• *预测: * “…London.” (因为也许模型认为叫 Paul Marston 的人通常出生在伦敦) 。
• *修正: * 在输出概率分布中，我们将分配给“Paul”的概率移回给“Wilhelm”。

为什么要换回来？如果不这样，遗忘后的模型可能会混淆主体是谁。我们希望模型说，“Wilhelm Wattenbach 出生在伦敦” (一个通用的、不正确的事实) ，而不是在被问及 Wilhelm 时说“Paul Marston 出生在伦敦”。

4. 聚合多个教师

原始 WHP 仅使用了一个替换名称。因果框架表明我们应该对许多 \(e\) (许多不同的人) 进行求和。

作者使用 \(N\) 个不同的名字 (例如，20 个随机名字) 运行上述过程，并对结果概率分布进行平均。

• *名字 1: * 预测 London。
• *名字 2: * 预测 New York。
• *名字 3: * 预测 Berlin。

当你将这些平均后，你会得到一个“平坦”的分布。模型变得不确定。它不再自信地撒谎；它只是不知道了。这个简单的聚合步骤被证明是防止幻觉的关键。

5. 训练学生

最后，我们训练学生 LLM (参数为 \(\theta'\)) 以最小化其自身预测与这个聚合教师分布之间的差异 (KL 散度) 。

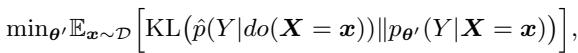
这个公式本质上是说: “调整学生模型 \(\theta'\)，使其在看到原始文本 \(x\) 时，输出与教师相同的困惑、通用的概率。”

实验与结果

为了证明这一点的有效性，作者构建了一个名为 WPU (Wikipedia Person Unlearning) 的全新、严谨的基准测试。

他们从维基百科中选择了 100 个真实人物 (非超级名人) 并创建了数据集来测试:

1. 遗忘问答 (Forget QA) : 关于目标的问题。
2. 强保留问答 (Hard-retain QA) : 关于目标传记中提到的其他实体的问题。
3. 通用保留问答 (General-retain QA) : 关于名人 (如埃隆·马斯克) 的问题，以确保通用能力。

WPU 上的表现

他们将他们的方法 (“Ours”) 与几个基线进行了比较:

• GA (梯度上升) : 只是试图最大化目标数据上的损失。
• WHP: 原始算法。
• Prompting (提示法) : 只是告诉模型“不要谈论这个”。

以下是五个关键标准的归一化性能:

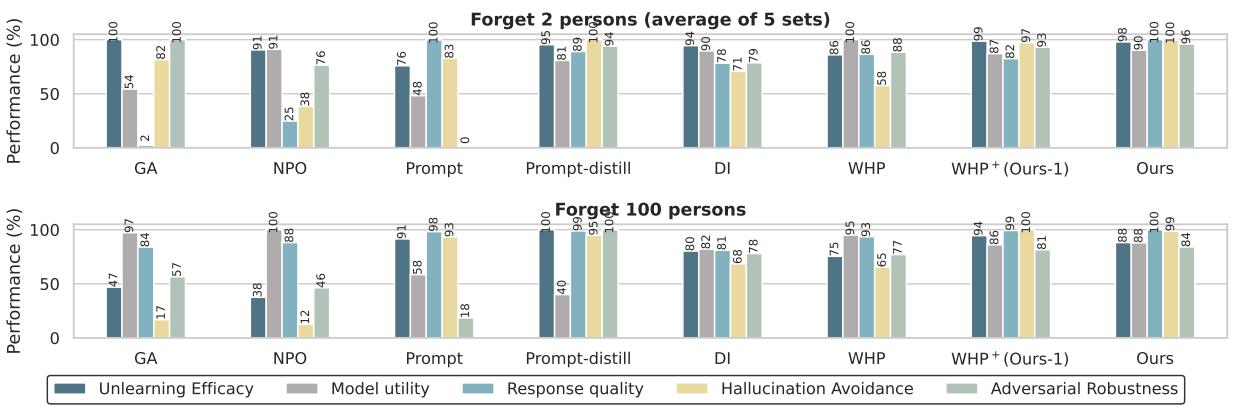
图 4 的关键要点:

• 遗忘效能 (深蓝色) : 提出的方法 (Ours) 几乎完美 (98%) 。它真正做到了遗忘。
• 响应质量 (青色) : 看看 GA (梯度上升) 。它的响应质量显著下降，因为最大化损失通常会让模型胡言乱语。因果方法保持了完美的质量。
• 避免幻觉 (黄色) : 这是一个巨大的胜利。原始 WHP (图中标记为 WHP) 在这里很挣扎，经常编造事实。新方法 (Ours) ，由于聚合了多个名字，实现了近乎 100% 的避免率。它正确地拒绝回答而不是撒谎。

TOFU 基准测试

他们还在 TOFU (Task of Fictitious Unlearning) 数据集上进行了测试，该数据集使用虚构的作者和书籍。这是一个受控环境，我们确切地知道“黄金标准” (一个从未接触过该数据、从头训练的模型) 是什么样子的。

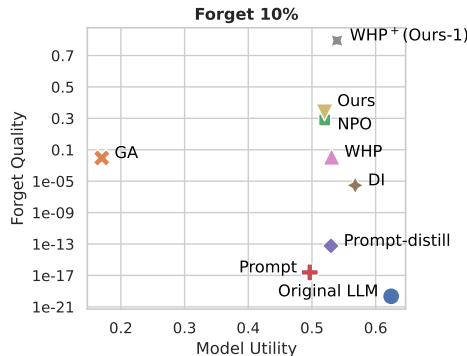
在图 5 中，我们希望处于右上角 : 高模型效用 (聪明的模型) 和高遗忘质量 (成功的遗忘) 。

• GA (橙色 X) : 效用高，但遗忘质量极差 (左下角) 。
• WHP (粉色三角形) : 稍好，但仍落后。
• Ours (灰色/黄色) : 因果方法以最好的方式成为了明显的离群点。它们实现了与原始模型相媲美的遗忘质量，同时保持了效用。

为什么“N”很重要？

回想一下，该方法涉及对 \(N\) 个替换名字的教师分布进行平均。这是必要的吗？

图 6 中的消融实验显示了增加 \(N\) (替换名字的数量) 的影响。

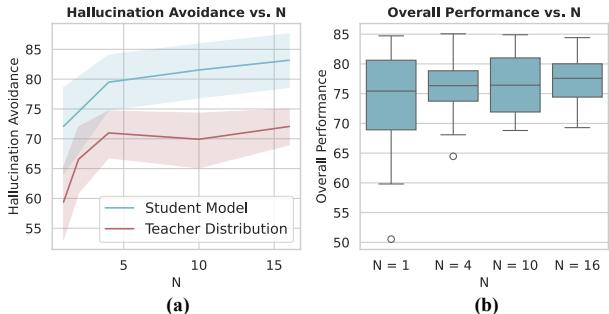
随着 \(N\) 增加 (x 轴) , 避免幻觉 (图 (a) 中的红线) 稳步上升。如果你只使用一个名字 (像原始 WHP 那样) ，模型可能会产生关于那个替换名字的具体细节的幻觉。通过平均 10 或 15 个名字，具体的细节相互抵消，留给模型的是关于目标的“平坦”知识库。它有效地学会了它不知道。

结论与意义

这项研究弥合了经验性“黑客技巧”与理论理解之间的差距。通过因果干预的视角审视遗忘问题，作者成功地解释了为什么替换名字有效: 这是估计反事实分布的一种实用方法，在该分布中特定实体的知识被移除。

最终得到的算法是:

1. 有效的: 它清除了特定数据。
2. 外科手术式的: 它保持相关概念完好无损 (定向遗忘) 。
3. 安全的: 它减少了困扰以前方法的幻觉问题。

随着围绕 AI 隐私和版权的法规日益严格 (例如“被遗忘权”) ，像这样的技术将变得至关重要。我们不能每次用户想要移除数据时都重新训练 GPT-4。我们需要能够对模型的“大脑”进行精确的、因果性的手术。这篇论文提供了这把手术刀。