引言: 神经网络拥挤的思维

如果你曾试图理解神经网络在“想”什么，你很可能遇到过一个令人困惑的现象，称为多义性 (polysemanticity) ——即单个神经元会对多个看似无关的概念产生激活。一个神经元可能同时对“猫”、“速度”和颜色“红色”做出响应。对于研究机制可解释性 (mechanistic interpretability) 的学者来说，这使得逆向工程网络变得极具挑战性。

对这种行为的一种主流解释是由 Chris Olah 及其合作者提出的叠加假设 (superposition hypothesis) 。 该假设认为，神经网络在其激活空间中打包的“特征”或概念远多于其维度——通过将特征编码为近似正交的方向，而不是分配给单个神经元。只要在任意时刻仅有少数特征是活跃的 (即表示是稀疏的 )，网络便能在不破坏可分性的前提下存储这些额外信息。

以往的研究主要将叠加视为一种存储机制——用于压缩表示并通过狭窄瓶颈传递信息的方式。但如果叠加不仅仅涉及存储呢？如果神经网络还能在叠加态中对特征进行计算呢？

这个问题是近期一篇理论论文 《叠加态计算的数学模型》 (Mathematical Models of Computation in Superposition) 的核心。该论文建立了一个严谨的数学框架，用于解释叠加态中的计算 。 作者们没有将叠加仅仅视为一种巧妙的编码技巧，而是展示了神经网络如何在特征保持压缩和纠缠的情况下，模拟复杂的逻辑电路。其结果为我们描绘了一幅蓝图，揭示了网络如何执行密集、高效的计算——并有可能重塑我们对现代人工智能如何“思考”的认知。

本文将解读论文的核心思想: 从特征表示的基础入手，介绍如何构建一个能让单层网络在叠加态下执行逻辑与运算 (AND) 的模型，最后探讨这种能力如何扩展以模拟整个深度电路。

背景知识: 什么是“表示”一个特征？

在深入讨论计算之前，我们需要先理解特征在神经网络中被表示意味着什么。假设我们有一个包含 d 个神经元的网络层，而其激活编码了 m 个二元特征，其中 m > d。对于输入 \( x \)，其激活向量可以写作:

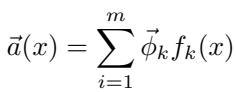
表示激活值作为特征向量之和的方程。

激活向量 \( \vec{a}(x) \) 是特征向量 \( \vec{\phi}_k \) 的和，并由每个特征是否存在 \( f_k(x) \) 加权。

挑战在于如何从这个纠缠的总和中解读出各个特征。为此，论文定义了不同层次的线性表示 (linear representation) , 用来衡量从激活中可靠提取特征值的能力。

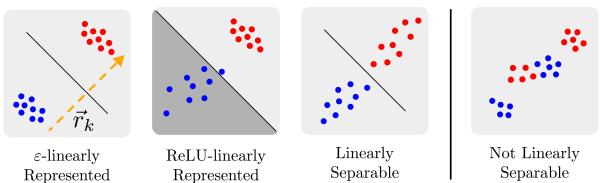
比较 ε-线性表示、ReLU 线性表示和线性可分特征的图示。

图 1: 不同强度的特征表示可视化。红色和蓝色点标示特征的有无。分离越紧密越清晰，表示越强。

  1. 弱线性表示 (线性可分) : 如果可以画出一个超平面，将“激活”与“非激活”的输入区分开，则该特征是弱线性表示的。这是一种最低限度的定义——仅保证可分性，而非可靠性。正负样本间的间距可以非常小，使这类特征在后续计算中易失效。

  2. ReLU 线性表示: 一种更强的形式，在以往研究中广泛使用。它表示特征可以通过将激活传入 ReLU 层并最小化输出与真实特征值之间的平均误差来读取。这能同时读取许多特征，但平均误差可能掩盖了特定输入下的糟糕表示。

  3. ε-线性表示: 本文使用的最强形式。如果对于每个特征，都存在一个向量 \( \vec{r}_k \)，使得它与激活的点积在每个输入上都与真实二元值的差异不超过 ε，那么该特征集是 ε-线性表示的。这保证了持续的精度，而不仅仅是平均正确性。

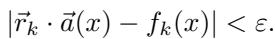
ε-线性表示的方程。

ε-线性表示要求，对于每个输入，读出向量与激活的点积始终紧密逼近 0 或 1。

满足这一严格标准的特征不仅可识别，而且可计算。一旦特征是 ε-线性表示的，逻辑运算如与 (AND) 、或 (OR) 也可以在后续层中被 ε-线性表示。弱表示则失去这种组合性 (compositional property) 。

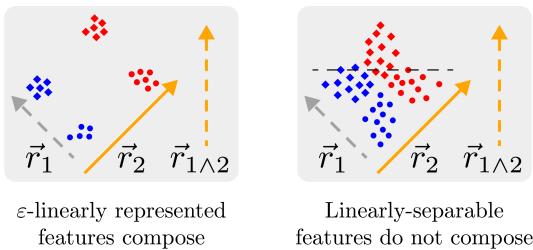
展示 ε-线性表示特征可组合而仅线性可分特征不可组合的图示。

图 2: 左侧，ε-线性表示的特征能可靠组合成新特征 (如与门) ；右侧，较弱表示模糊不清，无法组合。

通过这一形式化框架，作者展示了神经元在叠加态中不仅能存储，还能处理信息。

从表示到计算: 通用与门电路

论文的第一个主要构造解决了一个看似简单的任务: 计算所有可能特征对的逻辑与 (AND) 。给定 m 个输入特征，需要计算 \( \binom{m}{2} \) 个成对与门，即所谓的通用与门 (U-AND) 电路。

朴素方案

当输入是二元时，可以用一个 ReLU 神经元计算 \( x_i \wedge x_j \)，即 \( \text{ReLU}(x_i + x_j - 1) \)。最直接的网络会为每一对特征构造一个这样的神经元:

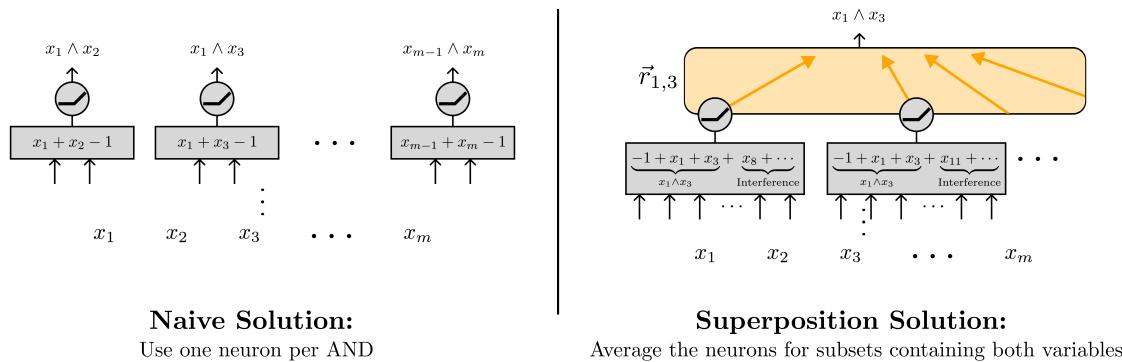
对比朴素“每个与门一个神经元”方案与更高效叠加方案的图示。

图 3: 左——朴素方案: 每对特征一个神经元，规模随 \( O(m^2) \) 增长。右——叠加方案: 每个神经元检查随机子集，大幅减少总数量。

这种朴素方法的规模随 \( O(m^2) \) 增长，简单但低效。

叠加方案

论文提出了一种优雅的重构方法，利用叠加与稀疏性实现显著的效率提升。

  1. 随机子集检查 每个神经元在一个随机子集中，如果至少两个输入开启，就激活，例如 \( \text{ReLU}(b_1 + b_3 + b_8 + \dots - 1) \)。 这样，每个神经元不再对应单一与门，而是对多组与门贡献分布式信号。

  2. 稀疏性 假设任意输入最多激活 s 个特征。稀疏输入限制了重叠子集的干扰。

  3. 平均读出 对于特定的特征对 \( (b_k, b_\ell) \)，通过平均那些子集同时包含这两个特征的神经元激活，可以复原它们的与运算。噪声在期望上相互抵消，留下真实的成对贡献。

数学证明表明，若神经元随机采样子集，干扰项随宽度 \( d \) 的增大而减小，网络可高精度地近似所有成对与运算。论文给出如下结论:

定理 2 (输入叠加态的 U-AND) : 一个单层 MLP 可用仅 \( d = \tilde{O}(\sqrt{m}/\varepsilon^2) \) 个神经元实现对 m 个特征的通用与门电路的 ε-线性表示——即使输入也处于叠加态。

这是一个惊人的结果。输出数量达 \( O(m^2) \)，但网络的宽度仅按 \( \tilde{O}(\sqrt{m}) \) 增长。计算丰富度剧烈上升，而不需额外神经元。

真实网络能实现吗？

令人惊讶的是可以。论文证明，即使随机初始化的网络也具备执行类似 U-AND 计算的能力。

定理 3 (随机初始化的 MLP) : 在层宽足够大的情况下，随机单层 MLP 以高概率 ε-线性表示通用与门电路。

换句话说，这种叠加计算并非脆弱巧合，而是标准神经网络架构的自然属性。网络天生具备这些密集逻辑运算能力；训练仅用于将干扰模式调谐为连贯的功能。

从 U-AND 到任意计算: 扩展框架

通用与门为通用计算奠定了基础。任何布尔函数都可表示为与项的组合 (即析取范式 )。通过高效计算成对乃至多路与门，网络可以模拟任意布尔电路。

高扇入与门

U-AND 的思想自然延伸至更高阶合取。通过调整神经元组合子集的方式，单层即可计算三元、四元乃至更多项的与门。每一与项仍保持 ε-线性表示。

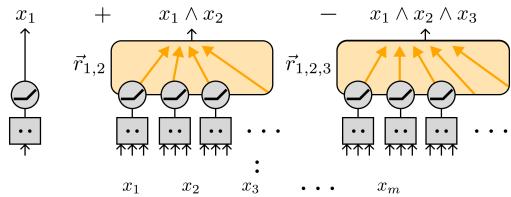
展示如何通过加减法组合特征合取以构造复杂函数的图示。

图 4: 构建更复杂的布尔电路。通过加法与减法组合与门，一个 MLP 可表示任意布尔特征组合。

作者证明:

定理 6: 对于任意深度为 L 的稀疏布尔电路，存在一个宽度为 \( \tilde{O}(\sqrt{m}) \) 的单层 MLP，可 ε-线性表示其输出。

唯一缺点在于，随着深度增加，计算所有可能的合取需指数级数量的神经元。

纠错机制的引入: 走向深度网络

为抑制这种指数级增长，研究者提出了交替使用U-AND 层与纠错层的结构。

  • 计算层: 执行逻辑运算 (如所有成对与门) 。
  • 纠错层: 清理累积干扰，在不扩展宽度的情况下恢复特征纯度。

每个纠错层将干扰 ε 减少到 ε/c，从而使噪声在网络深度上保持有界。

定理 8: 任何宽度为 m、多项式深度为 L 的稀疏布尔电路，都可由一个深度为 \( 2L \)、宽度 \( d = \tilde{O}(m^{2/3}s^2) \) 的深度神经网络实现 ε-线性表示。

这一结果完善了框架: 在叠加态中进行深度计算，紧凑编码并持续自我纠错。

对机制可解释性的启示

这些数学构造对理解真实神经网络具有重要意义。

1. 警惕“未使用”的特征

随机网络能自然表示复杂逻辑合取这一事实表明，网络中也许存在许多可识别但“无用”的特征。线性探针与稀疏自动编码器可能会发现对应于某些“概念”的方向，仅因它们在数学上可存在——而非被实际用于计算。一个特征可检测并不意味着它被使用。

2. 寻找纠错模式

高效的叠加计算需要纠错机制。执行类似压缩计算的真实网络可能包含稳定化激活的非线性层——可将受到噪声影响的表示重新拉回一致状态。近期机制可解释性研究的实证发现 (例如 GPT-2 中观察到的激活“平台现象”) 或许已经暗示了此类结构的存在。

局限性与未来方向

尽管这一模型优雅，但仍存在限制:

  • 仅限二元特征: 真实神经网络处理的是连续或多值特征，而非纯粹布尔值。
  • 稀疏性假设: 理论优势依赖稀疏激活。常见的 Transformer 或视觉模型是否满足这一条件仍有待验证。
  • 理想化读出: ε-线性表示的假设较强，可能过度简化真实特征间的交互。

未来研究可将这些结果拓展到连续或概率特征空间，放宽稀疏性假设，或将框架应用于实证数据。

结论

《叠加态计算的数学模型》将叠加从被动的存储现象重新定义为主动的计算机制。通过通用与门及其拓展，作者展示了网络如何在低维空间中对压缩特征执行庞大的逻辑运算——远比朴素架构所需的神经元更少。

本质上，论文告诉我们: 在神经网络拥挤的思维中，计算未必发生在神经元之间，而是发生在它们共同表示的叠加特征云之内。理解这一隐藏的逻辑层，也许是揭示 AI 系统如何真正处理信息的关键。